Тема 11. Теория потребительского спроса.

1. Товары – заменители, предельные нормы замещения

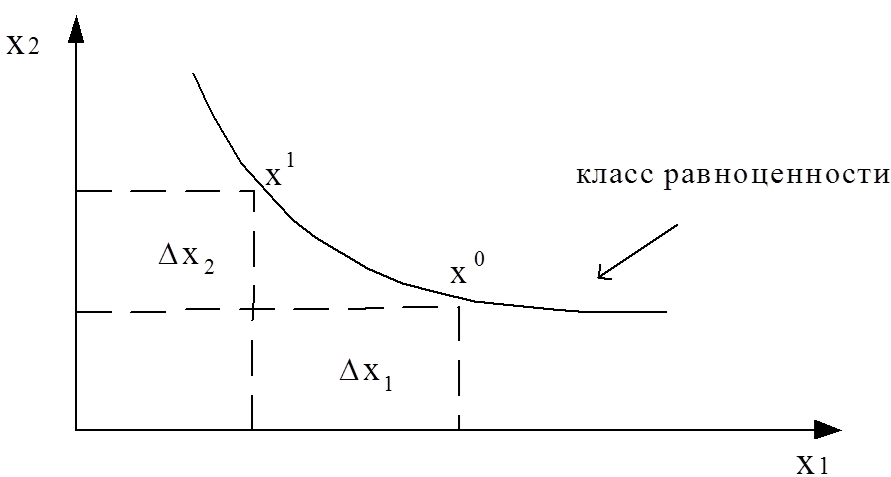
Пусть существуют различные наборы товаров (из некоторого списка), имеющих одинаковое значение функции полезности U(x). Например: для двух товаров х₁, х₂, составляющих множество Х⁰=(x₁,х₂), можно отыскать множество Х¹, имеющее то же значение функции полезности.

Функция полезности:

Т.е. у X¹ и X⁰ одинаковое значение функции полезности. Уменьшение товара х₁ при переходе к X¹ на величину Δх₁ компенсируется в функции полезности увеличением количества товара х₂ на Δх₂. Отношение 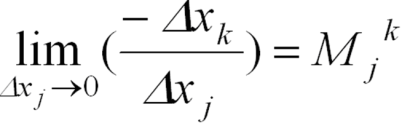- называется предельной нормой замещения i-го товара k-м товаром.

Более общее выражение: 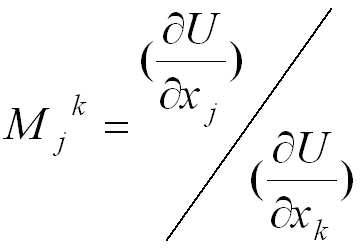- есть предельная норма замещения

2 Задача оптимизации выбора потребителя

Задача потребителя – найти набор товаров Х=(х₁, х₂, … , х_n), который максимизирует функцию полезности U(х₁, х₂, … , х_n), при наличии бюджетного ограничения

где x_i ³0;

p_i – цены на товар;

Q – бюджет или доход потребителя.

Решение задачи:

Искомая точка максимума х^* лежит на границе бюджетного множества (принимаем без доказательства как аксиому), тогда для набора из двух товаров можно изобразить график Рисунок – Построение кривых безразличия

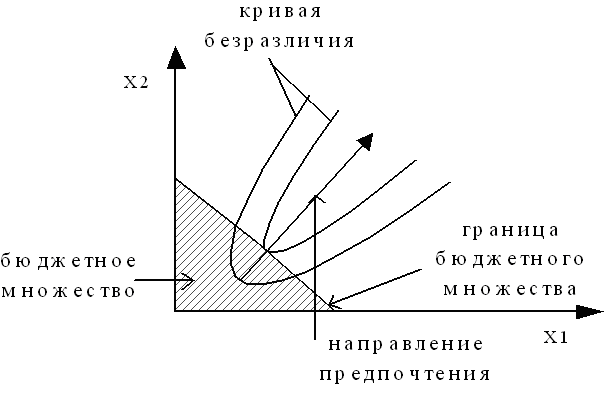
Бюджетное множество (ниже косой черты) объединяет наборы товаров, для которых выполняется бюджетное ограничение. Ряд кривых безразличия, объединяющих наборы товаров с некоторым одинаковым значением функции полезности, пересекает границу бюджетного множества. Таким образом, максимальное значение функции полезности достигается в точке х^*, которая лежит на направлении увеличения предпочтения (увеличение полезности) и лежит на границе бюджетного множества.

х^* - называется точкой спроса или просто спросом потребителя, х^* является решением поставленной задачи. В точке спроса х^* - предельная норма замещения j-го товара i-м = обратному соотношению цен товаров.

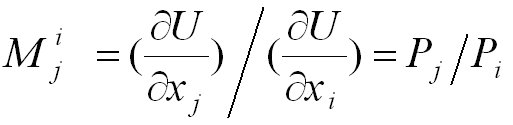
т.е. в точке оптимального выбора наборов, при данном бюджетном ограничении, полезность замещения товаров определяется соотношением цен товаров.

3 Функция спроса

Точка спроса х^* - есть функция от вектора цен Р и дохода Q. Функция, рассчитывающая точку спроса по данным аргументам, называется функцией спроса. Фактически данная функция задается как система функций, рассчитывающих компоненты вектора Х^*, т.е.

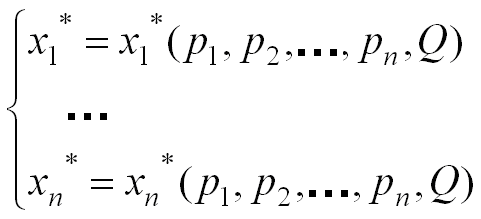
В этом выражении х_i^*() – обычные функции (не векторные), задающие оптимальное количество товара некоторого наименования в товарном наборе (в корзине потребления) при данном бюджетном ограничении. Они носят наименование функции спроса соответствующих товаров.

Ряд характеристик функции спроса имеет самостоятельное значение и используются в более сложных моделях спроса (уравнение Слуцкого), в частности важной характеристикой является частная производная вектор функций х^* по Q :

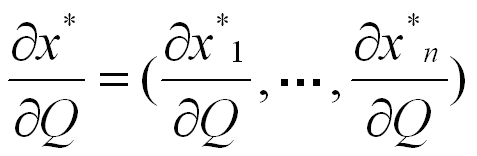
т.е. частная производная функции полезности по размеру дохода Q – есть вектор частных производных функций спроса соответствующих товаров по доходу Q.

4 Уравнение Слуцкого

 В исследовании функции спроса и вообще в теории потребления основополагающую роль играет уравнение Слуцкого:

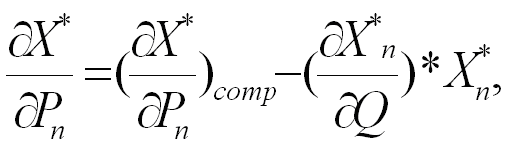
Слева - производная функции спроса по цене n-го товара, т.е. изменение точки спроса при изменении цены n-го товара при неизменных ценах прочих товаров и неизменном доходе Q.

В правой части уравнения рассматривается изменение точки спроса при изменении дохода Q, здесь X^*_n – это функция спроса на n-й товар.

Выражение

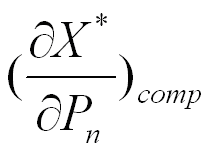- определяется следующим образом:

1) Изменяем р_n на величину Δр_n, что повлечет изменение функции спроса Х^* в новое значение Х', т.е. получим изменение спроса Х'- Х^*, Q при этом неизменно, т.е. изменяется значение максимальной полезности;

2) В связи с этим изменяем доход Q так, чтобы значение максимальной полезности в новой точке спроса Х' не изменилось;

3) Определим соответствующие отношения

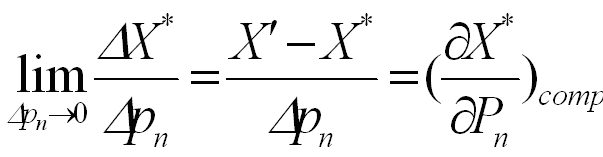
Примечание:

Можно рассматривать не различные наборы товаров, а различные единичные товары с отличным набором значений свойств.

В этом случае задача ставится так:

- Найти из ряда возможных товаров тот, который обладает максимальной полезностью при заданном бюджетном ограничении, т.е. максимальной суммой, выделяемой на покупку товара.

Условие:

- Перейти к новой функции полезности, взяв вместо модуля – квадратную степень;

- Перейти к трем неформальным свойствам, прочие – опустить;

- Поскольку цен (в обычном смысле слова) у свойств нет, то рассчитать их, взяв 5-6 известных товаров данного класса с их ценами на данный момент времени (число неизвестных не совпадает с числом уравнений);

- Взять три бюджетных ограничения (в интервале возможных цен) - Q;

- Найти для каждого ограничения точку касания;

- Еще 2 раза изменить цены, взяв 5-6 известных товаров данного класса с их ценами на в прошлые периоды времени и рассчитать цены свойств;

- Рассчитать по три точки касания по Q;

- По девяти точкам касания путем регрессии построить три функции спроса на качества товара как функции от Q и P1, P2, P3;

- Построить графики с вектором направления предпочтения.