2. Метод анализа иерархий (маи) для формирования оценок ряда трудноформализуемых факторов

– оценка важности того или иного критерия для данного класса потребителей;

– вес того или иного значения неформального качества.

Основа метода МАИ – это таблица попарных сравнений важности.

Тут критерий 2 важнее критерия 1 в три раза, а критерий 1 менее важен критерия 2 в три раза. Матрица обратно симметрична. В данной матрице вполне допускаются противоречия, что не позволяет построить шкалу оценки важности критериев обычными способами. Аналогично строится матрица для значений трудноформализируемых параметров. Различные значения параметра, например, цвета, связаны с некоторыми альтернативами оцениваемого товара А, В… напр, авто(«мерседес-зеленый»)

Критерий 2 обрабатывается аналогично.

В соответствии с методом МАИ для упорядочивания критериев или неформальных качеств альтернатив товаров на основе матриц попарных сравнений применяется подход, основанный на расчете нормированнх собственных векторов матриц.

Т.е считается, что искомое упорядочивание мн-во числовых значений сравниваемого параметра – это нормированный собственный вектор матрицы попарных сравнений. Пусть дана квадратная матрица

и характеристический многочлен для оператора, заданного матрицей А.

Фактически, этот оператор есть некоторое степенно выражение относительно .

Характеристическое уравнение оператора А имеет вид:

Где любые значения , являющиеся корнем этого уравнения, называются собственным значением оператора А.

Выберем из множества корней некоторое действительное .

Если существет вектор размерностью «n» не нулевой и являющийся решением уравнения , то называется собственным вектором оператора А.

Нормой вектора Х называется число равное корню квадратному из суммы квадратов координат этого вектора.

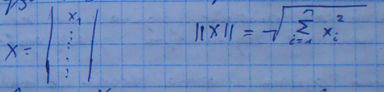
Вектор Хн называется нормированным, если получается путем деления всех координат некоторого Вектора Х на его норму

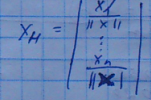Проделав с помощью Маткад след действия:

- найдя детерминант как многочлен от лямбда

-решив характеристическое уравнение и найдя корень ( действетельный) лямбда итое)

-Для Лямбдаитое собственный вектор;

-нормируем вектор

Полученный нормированный вектор есть вектор весов альтернатив или критериев. В частности, на основе таблиц попарных сравнений критериев получаем вектор коэф-в Аитое, использ. В ф-ции полезности.

Вектор коэф-в аi номер критериев

Коэф-т важности критерия ai

Аналогичные действия нужно произвести для всех неформальных параметров, значение не явл. Числами, а являются словами. Таким образом получается числовые значения xi^n для неформ. параметров

Для формальных параметров нет смысла строить матрицу попарных сравнений и рассчитать собственный вектор т.к. мы имеем уже и числовые значения.

Т.е. расматривается исходные формальные параметры и неформальные параметры преобразованные к числам. Полученные оценки можно свести в таблицу «товары-свойства» и найти свойства идеального товара.

Табл. 2.3. Вектора оценок качества товаров по критериям

Далее по полученным рассчитываем показатели качества и находим лучший товар по минимальному значению показателя качества, т.е определяем его как самый близкий к идеалу.

Мы как потребители хотели бы его купить а как производители хотели бы производить, поскольку этого товара самые высокие шансы быть купленной данной категории покупателей.