2. Функция полезности и её свойства

2.1 Определение функции полезности.

Удобно и желательно оценивать привлекательность товара количественно, т.е приписывать каждому набору Х из пространства С некоторое число U(X).

Главное требование к таким функциям – это отображение отношений слабого предпочтения на С, т.е. функция U(X) должна удовлетворять требованиям:

U(X) ≤ U(Y) <=> X ≤ Y

U(X) < U(Y) <=> X < Y

U(X) = U(Y) <=> X = Y

Такая функция называется функцией полезности. Работать с ней удобней, чем с системой предпочтений. Условия, при которых сущ. ф-ция полезности определяется след. теоремой:

Теорема Габре:

Если система предпочтений непрерывна, то сущ. непрерывная функция полезности.

Примечание. Функция полезности не явл. уникальной, т.е. для данной системы предпочтений можно составить мн-во ф-ций полезности.

2.2. Свойства функции полезности.

1) Она неубывающая, т.е. если X ≤ Y, то это влечет за собой U(X) ≤ U(Y).

2) Она дифференцируема, т.е. сущ. частные производные от функции полезности U(X) по всем Xi (количество i-го товара) в пространстве C(X).

Определение. Частная производная называется предельной полезностью i-го товара (Xi) в т.X пространства С(Х).

Из свойства неубывания функции полезности следует, что данная производная >0 для всякого товара, т.е. предельная полезность каждого товара Xi>0.

С точки зрения экономики это трактуется, как желание пользователя приобретать i-й товар даже при наличии у него набора товаров X.

Вектор размерностью N, состоит из частных производных функций полезности U(X) по отдельным товарам Xi - ( , …. ,) – называется вектором предельной полезности и обознач. как

Для более полного использования мат.аппарата от функции полезности требует, чтобы:

1) функция полезности была дважды дифференцируема;

2) матрица сост. из вторых частных производных функций полезности (матрица Гессе) была отриц. Определена в любой точке.

Вид матрицы Гессе:

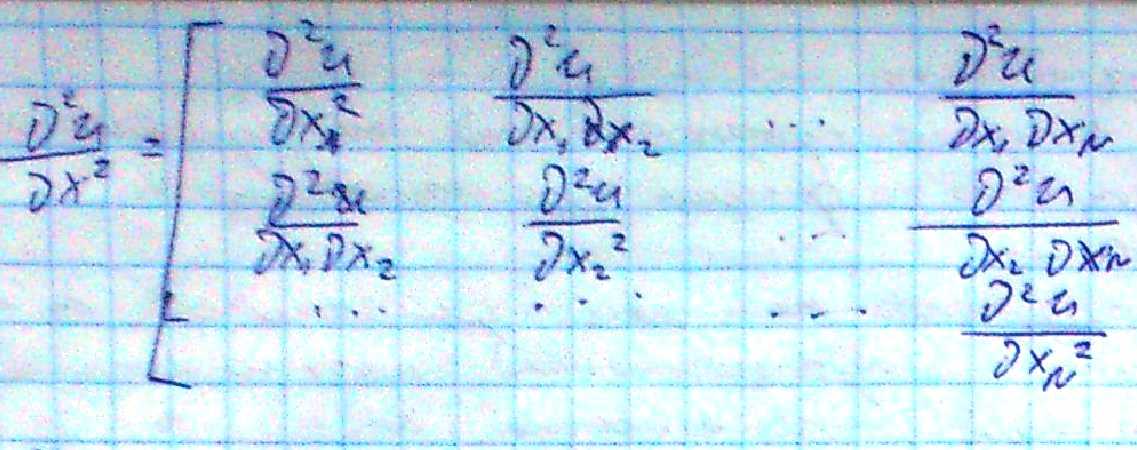
Отрицательная определенность предполагает, что <0 i=1,..N,т.е.верно след. утверждение

1. Закон Госсена. Предельная полезность товара уменьшается по мере увеличения его потребления. На практике функцию полезности выбирают исходя из соотв. реальных факторов и наблюдений.

Рассмотрим некоторые функции полезности, соотв. данным допущениям.

1) Неоклассическая. U( ) = , при этом α, β > 0 , α+β < 1.

2) Квадратическая. 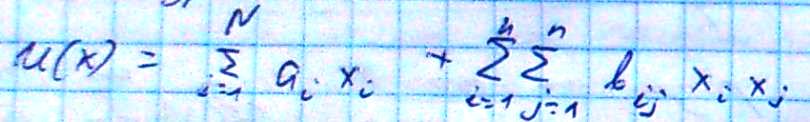, где матрица В= отрицательного определена и +

3) Логарифмическая. U(Х) = , где ≥0 , при этом основание логарифма – любое число.

Тема 10. Эвристические методы построения функции полезности

1. Общий подход к решению задачи построения эвристической функции полезности.

Эвристический подход позволяет построить необходимую функцию полезности, ориентированную на данный товар. Построение функции полезности зависит от мотивации покупателя той или иной категории, типов отдельных критериев – лекго формализуемые или трудноформализуемые.

Определяющим фактором является оценка качества товара со стороны покупателя, включая:

-соотв. Потребительским требованиям

-престижность модели

-высокие технические и эргономические показатели

-низкая стоимость

-соответствие финансовым возможностям и др.

Тут названы критерии любого типа

Рассмотрим для примера проблему выбора счетчиков для домов и квартир как оценку мотивации категории покупателей с низким уровнем доходов.

Случайные события:

-желание установить счетчик,

-Соотв. Стоимости семейному бюджету;

-влияние неопределнностей внешней среды и т. Д.

Критерий – «соответствие стоимости семейному бюджету» может иметь значение 1 или 0 при следующих условиях

Критерий равен 1, если

Для принятия решения предлагается ввести понятие идеального изделия

Оценку уровня качества к-го изделия некоторой группы можно подсчитать как

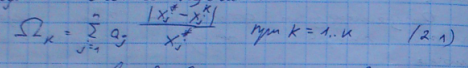
Где aj – множество весовых коэффициентов позволяющих учесть уровень важности параметра. При этом имеет место зависимость «качество высокое->низкое »

(какая то буква) искомая функция надежности есть фактически вариант штрафной функции, которая для идеального товара стремится к 0. Вариант аналогичной функции, имеющий вид полинома второй степени:

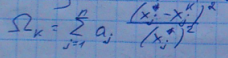
Экстремум параметра, соответствующий идеальному товару, это лучшее желаемое значение параметра ( например мин. Цена, макс срок службы и т д)

Экстремум мб как минимумом так и максимумом

Получение оценок в случае наличия и формального представления не является трудной задачей. Сложнее дело обстоит в случае трудноформализуемого типа параметра, значения которого, как правило, задаются словами.

Например:

1) вкус – сладкий, соленый…

2) цвет – красный, синий…

3) дизайн – классический…

4) форма – овал, квадрат…

5) комфортность

Рассмотрим соотв. Возможные методы оценки трудноформализуемых параметров.