О силах, действующих в жидкости

Различают три вида сил – сосредоточенные, действующие в точке, которые встречаются в МЖГ в исключительных случаях, распределенные (по объему), действующие на каждый элемент объема V (или массы) и поверхностные, действующие на каждый элемент поверхности.

Объемные силы , где - главный вектор массовых сил.

Массовые силы (плотность массовой силы) , т.е.

и имеют размерность силы, - размерность ускорения, а - размерность ускорения умноженную на размерность плотности:

[ ]=[м/с^2], [ ]=[м/с^2]*[кг/м^2]

Примеры массовых сил – сила тяжести, силы инерции, вводимые в неинерциальных системах отсчета (Кориолисовы, центробежные); электромагнитные силы.

Поверхностные силы.

Основные силы, играющие роль в механике сплошной среды. Это распределенные силы по поверхности выделенного элемента: - плотность поверхностных сил , действующих на площадку . Соответственно [Н/м^2]

Силы внутренние и внешние

Силы называются внутренними, если они вызваны объектами, принадлежащими системе, движение которых рассматриваются и внешними, если они вызваны внешними по отношению к данной системе объектами. Это разбиение в целом – условное, одни и теже силы в зависимости от рассмотрения могут считаться как внутренними, так и внешними.

Силы внутренних напряжений

…

Рассмотрим объем V с поверхностью F и разобьем его на две части поверхностью S с элементарными площадками и ориентированных по . Таких площадок можно провести сколько угодно и действие одной части на другую заменить поверхностными силами , где плотность поверхностных сил. Такие силы называются силами внутренних напряжений. Их можно разложить на нормальные по нормали к и касательные , лежащие на поверхности S

Если S – твердая поверхность, то эти поверхностные силы будут внешними.

Уравнение количества движения для сплошной среды.

Производная по времени количества движения объема V сплошной среды равна сумме всех действующих на него массовых и поверхностных сил.

- для системы материальных точек.

Для жидкой частицы массы :

а для всего выделенного объема V:

Введем массовые и поверхностные силы с напряженностью и соответственно, тогда: (*)

В такой форме уравнение количества движения записывается для сплошной среды и называется уравнением движения в напряжениях в интегральной форме. Уравнение справедливо для непрерывных и разрывных функций внутри выделенного объема.

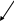
Для перехода к дифференциальной форме необходимо вначале интеграл по поверхности свести к интегралу по объему.

y

dSx =dydz – элем. площадка

x

z dx dz

По теореме Остроградского – Гаусса

, где - поверхностная сила, отнесенная к единице объема. Полагая непрерывность всех функций внутри выделенного объема в уравнении (*) можем перейти к уравнению движения в напряжениях в дифференциальной форме:

В проекции на оси координат