Лекция №1 Введение Газовая динамика и ее место в механике сплошных сред.

Газовая динамика описывает процессы, происходящие в газах при их взаимодействии с твердыми телами. Сюда относятся:

1. процессы в энергетических установках и двигателях (поршневых, газотурбинных, ракетных и др.)

2. движение тел в газах (самолетов, снарядов, метеоритов и др.)

Если рассматривается движение газов внутри каналов, трубопроводах, (т.е. ограниченное твердыми стенками) то этот процесс называется внутренней газодинамикой, если рассматриваются отдельные тела, движущиеся в газе, (или влиянием ограничивающих стенок можно пренебречь) то говорят о внешней газодинамике (аэродинамике).

Газовая динамика является самостоятельным разделом механики сплошных сред.

Механика сплошной среды

Механика жидкости Механика твердого Электродинамика

и газа (МЖГ) тела

Гидромеханика Газодинамика Сопромат Обработка

(гидродинамика) (ГД) материалов …

…

Гидродинамика ГД ГД ГД струйных

насосов и гидротурбин лопаточных каналов течений

машин

Понятие сплошной среды. Поля.

Любое вещество состоит из отдельных частиц, атомов и молекул; размеры атомов порядка см. Эти частицы находятся в постоянном движении. В жидкостях и газах они могут перемещаться в пределах всего занимаемого жидкостью объема, в твердых телах они колеблются около точек пространства, фиксированных относительно выделенного объема. Перемещение атомов (молекул) газа характеризуется их средней скоростью С и длиной свободного пробега молекул (которую они проходят до столкновения). Например: для воздуха и .

Однако при рассмотрении движения около тел, размеры которых значительно больше длины свободного пробега, можно пренебречь фактическим (молекулярным) строением жидкости (газа) и рассматривать их как сплошную среду, занимающую все рассматриваемое пространство.

Поле

Все физические характеристики сплошной среды считаются непрерывно распределенными по объему, образуя соответствующие поля (поля давлений, температур, концентраций, завихренностей, скоростей, ускорений и т.д.).

Введение понятий сплошной среды с определенными свойствами позволяет упростить и обобщить полученные результаты. С этой точки зрения твердое тело и жидкость- сплошные среды с разными свойствами. Исходным для них является уравнение нагруженности в напряжениях.

Модели сплошных сред.

Рассмотрим некоторые модели сплошных сред. Вначале определим границу, разделяющую сплошную среду от разреженной, которую оценивают по величине критерия Кнудсена , где L-характерный размер тела. Определение типа среды в зависимости от критерия Кнудсена приведено в таблице 1.

Число Кнудсена Kn	Тип среды
<0,01	Сплошная среда, течение происходит с «прилипанием»
0,01…0,1	Разреженная среда
0,1…10	Среда, в которой течение происходит со «скольжением»
>10	Свободномолекулярное течение

Условие прилипания заключается в том, что при движении твердого тела в жидкости (и наоборот) скорость жидкости на поверхности тела считается равной скорости поверхности тела. При движении со скольжением это равенство нарушается.

Сжимаемые и несжимаемые среды (жидкости и газы).

Сжимаемость характеризуется модулем сжатия К, который представляет собой отношение изменения давления к относительному изменению объема:

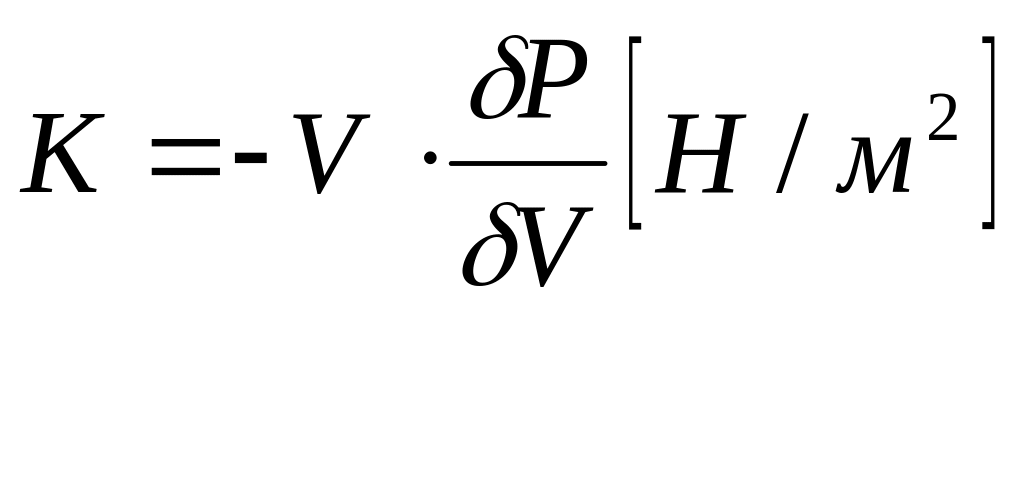
Все реальные жидкости сжимаемы, но если для воды , то для воздуха , т.е. для воздуха модуль сжатия в 22000 раз меньше модуля сжатия воды. При изотермическом сжатии, используя уравнение состояния PV=RT, получим , откуда , т.е. модуль сжатия газа при T=const равен давлению. При адиабатном процессе , где . Модуль сжатия К зависит от закона, которому подчиняется газ (уравнения состояния Ван-дер-Ваальса, Больцмана, Соава, Дитеричи и др.)

Для движущихся газов сжимаемость оценивают по числу (критерию) Маха, равного отношению скорости движения струйки к местной скорости звука , т.е. .

Скорость звука можно выразить через коэффициент сжимаемости:

Тогда число Маха будет зависеть от коэффициента сжимаемости. Экспериментальные данные показывают, что сжимаемость начинает проявляться при М>0,4 до этой скорости эффекты, связанные с сжимаемостью, можно не учитывать. В МЖГ газом называют сжимаемую жидкость.

Свойства текучести.

Если жидкость (или газ) заполняет какой-либо объем, то она принимает форму этого объема. Если изменить форму объема, то вместе с ним изменится и форма жидкости.

Неограниченное изменение первоначальной формы выделенного жидкого объема под действием приложенных к нему внешних сил называется текучестью .

Возникновение касательных напряжений. Реологические законы.

Если изменение объема происходит с конечной скоростью жидких частиц и эти скорости не постоянны, между слоями жидкости, движущимися с разными скоростями, возникают касательные напряжения пропорционально градиенту скорости.

Пример: две пластины, одна из них движется со скоростью V, другая неподвижна. При ламинарном течении изменение скорости между пластинами происходит по линейному закону (рис.1). Такое течение называется течением Куэтта.

V

Y

X

Касательные напряжения между слоями (1)

где -коэффициент пропорциональности, называемый коэффициентом динамической вязкости. Зависимость (1) установил И.Ньютон, и жидкости, подчиняющиеся данной закономерности, обычно называются Ньютоновскими. В общем случае зависимость между скоростями и касательными напряжениями имеют более сложный вид и устанавливаются экспериментально, например, для случая на рис.1

(2)

где -предельное начальное напряжение сдвига, при текучесть отсутствует и жидкость ведет себя как твердое тело ( ). (вязкопластические жидкости-лаки, краски, цементные растворы и др.)

Зависимости, выражающие нелинейную связь между касательными напряжениями и деформациями, называются реологическими законами, а жидкости - неньютоновскими.

Для коэффициентов вязкости различных сред существуют таблицы и формулы, в зависимости от параметров. (В технических расчетах коэффициент вязкости большинства газов зависит только от температуры). Если вязкость жидкости равна нулю и ей можно пренебречь, то такая жидкость называется идеальной в гидродинамическом смысле.