16. Формулы напряжений сигма и тао при изгибе
.
Согласно последнему выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называемых главными, а сами напряжения главными напряжениями.
Сопоставляя
выражения 
и 
,
имеем:
,
откуда и следует, что касательные напряжения на главных площадках всегда равны нулю.
В заключение, с учетом известных тригонометрических тождеств:
и
формулы 
,
определим
главные напряжения, выражая из через 
и 
:
.
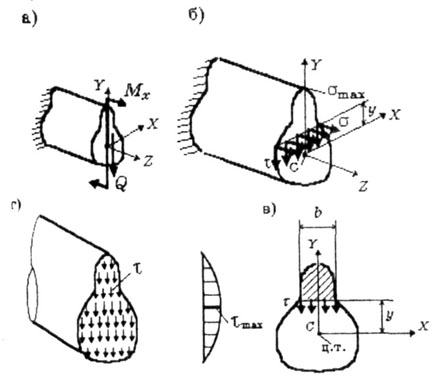
Во всех точках поперечного сечения бруса при поперечном изгибе возникают нормальные и касательные напряжения (на рис. 5.1,6 эти напряжения показаны в точках, отстоящих на расстоянии Y от оси X): |
|
Рис. 5.1 |
Условные обозначения. |
Mx, Q - внутренние усилия: изгибающий момент и поперечная сила, они изменяются вдоль бруса и определяются с помощью построения эпюр; |
у - координата точек поперечного сечения, в которых определяются напряжения; |
b - ширина сечения в месте определения касательных напряжений; |
Jx - главный центральный момент инерции -момент инерции относительно центральной оси х, |
сx* - статический момент относительно нейтральной оси ж той части площади поперечного сечения, которая расположена выше (или ниже) продольного сечения - выше или ниже уровня у, в точках которого определяются касательные напряжения. |
|
Эти формулы выведены в главных центральных осях поперечного сечения бруса. На рис. 5.1 это оси X, У. При этом ось Y совпадает с осью симметрии сечения, а ось X, перпендикулярная плоскости изгиба, проходит через центр тяжести сечения и является нейтральной осью: нормальные напряжения в точках этой оси равны нулю. Ось Z - ось бруса. |
Таким образом, на уровне у напряжения, определяемые вышеприведенными формулами, постоянны, не зависят от координаты X. |
С увеличением координаты у нормальные напряжения увеличиваются и в наиболее удаленных от нейтральной оси точках достигают наибольшего значения: |
|
Для расчетов используется специальная геометрическая характеристика - момент сопротивления сечения при изгибе: |
|
Касательные напряжения, наоборот, уменьшаются и в наиболее удаленных от нейтральной оси точках обращаются в нуль, а а области нейтральной оси достигают наибольших значений (рис. 5.1,г). Кроме того, наибольшие значения касательных напряжений значительно меньше максимальных значений нормальных напряжений: так для консольного стержня прямоугольного поперечного сечения, нагруженного сосредоточенной силой на свободном конце, отношение максимальных значений этих напряжений |
|
где l, h - длина бруса и высота его поперечного сечения. |
Поэтому, при l >> h, что имеет место в большинстве случаев, касательные напряжения по сравнению с нормальными пренебрежимо малы и при расчетах на прочность не учитываются. |
Условие прочности имеет следующий вид: |
|
|
-
допускаемое напряжение.