2.Теплопроводность через однослойную цилиндрическую стенку (стационарный режим).

Температуры поверхностей стенки –t_ст1 и t_ст2. Плотность теплового потока:

q = -λ∙ ∂t/∂n = - λ∙ ∂t/∂x = - λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙ или q = λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙ t/x (9.13)

Тогда

q = λ/δ∙(t_ст1 – t_ст2) = λ/δ∙Δt, (9.14)

Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м²∙К)/Вт], то плотность теплового потока:

q = (t_ст1 – t_ст2)/R . (9.15)

Общее количество теплоты, которое передается через поверхность F за время τ определяется:

Q = q∙F∙τ = (t_ст1 – t_ст2)/R·F∙τ . (9.16)

Температура тела в точке с координатой х находится по формуле:

t_x = t_ст1 – (t_ст1 – t_ст2)∙x/ δ . (9.17)

3.Вывод чисел подобия (Фруда и Эйлера).

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13

1.Дифференциальное уравнение теплопроводности.

.

2.Основы теории конвективного теплообмена.

Передача теплоты конвекцией осуществляется перемещением в пространстве неравномерно нагретых объемов жидкости или газов. В дальнейшем изложении обе среды объединены одним наименованием — жидкость. Обычно при инженерных расчетах определяется конвективный теплообмен между жидкостью и твердой стенкой, называемый теплоотдачей. Согласно закону Ньютона—Рихмана, тепловой поток Q от стенки к жидкости пропорционален поверхности теплообмена и разности температур между температурой твердой стенки t_c и температурой жидкости t_ж:

.

(10.1)

Главная трудность расчета заключается в определении коэффициента теплоотдачи α, зависящего от ряда факторов: физических свойств омывающей поверхность жидкости (плотности, вязкости, теплоемкости, теплопроводности), формы и размеров поверхности, природы возникновения движения среды, скорости движения.

По природе возникновения различают два вида движения — свободное и вынужденное. Свободное движение происходит вследствие разности плотностей нагретых и холодных частиц жидкости, находящейся в поле действия сил тяжести; оно называется также естественной конвекцией и зависит от рода жидкости, разности температур, объема пространства, в котором протекает процесс.

Вынужденное движение возникает под действием посторонних побудителей (насоса, вентилятора, ветра). В общем случае наряду с вынужденным движением одновременно может развиваться и свободное. Относительное влияние последнего тем больше, чем больше разность температур в отдельных точках жидкости и чем меньше скорость вынужденного движения.

Движение жидкости может быть ламинарным или турбулентным. При ламинарном режиме частицы жидкости движутся послойно, не перемешиваясь. Турбулентный режим характеризуется непрерывным перемешиванием всех слоев жидкости. Переход ламинарного режима в турбулентный определяется значением безразмерного комплекса, называемого числом Рейнольдса:

,

где w – скорость движения жидкости; ν — коэффициент кинематической вязкости¹; l — характерный размер канала или обтекаемой стенки.

При любом режиме движения частицы жидкости, непосредственно прилегающие к твердой поверхности, как бы прилипают к ней. В результате вблизи обтекаемой поверхности вследствие действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от нуля на поверхности тела до скорости невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости получил название гидродинамического пограничного слоя. Толщина этого слоя возрастает вдоль по потоку, так как по мере движения влияние вязкости распространяется все больше на невозмущенный поток. Однако и в случае турбулентного пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором носит ламинарный характер. Этот слой называется вязким, или ламинарным, подслоем.

Аналогично понятию гидродинамического слоя существует понятие теплового пограничного слоя — прилегающей к твердой поверхности области, в которой температура жидкости изменяется от температуры стенок t_с до температуры жидкости вдали от тела t_ж. В общем случае толщины гидродинамического и теплового пограничных слоев пропорциональны, а для газов практически равны.

Интенсивность переноса теплоты зависит от режима движения жидкости в пограничном слое. При турбулентном пограничном слое перенос теплоты в направлении стенки обусловлен турбулентным перемешиванием жидкости. Однако непосредственно у стенки, в ламинарном подслое теплота будет переноситься теплопроводностью. При ламинарном пограничном слое теплота в направлении стенки переносится только теплопроводностью.

3.Вывод чисел подобия (Фруда и Рейнольдса).

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14

1.Краевые условия теплопроводности.

.

(9.12)

Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Коэффициент температуропроводности a является физическим параметром вещества. Из уравнения (9.12) следует, что изменение температуры во времени для любой точки тела пропорционально величине a.

9.4.2.Краевые условия

Дифференциальное уравнение (9.12) описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые характеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает про­цесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды t_ж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

,

(9.13)

где t_c — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·К). Коэф­фициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,

.

(9.14)

Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:

.

Переписав последнее уравнение в виде:

,

(9.15)

получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.

2.Назначение оребрения. Коэффициент оребрения.

3.Вывод чисел подобия (Архимеда и Грасгафа).

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 15

1.Физические свойства жидкости.

1. Основной механической характеристикой жидкости является плот­ность , определяемая для однородной жидкости отношением ее массы m к занимаемому объему , кг/м3:

Плотность однородной жидкости одинакова во всех точках. Для определения плотности служат ареометры.

2. Вес жидкости, приходящийся на единицу объема, называется удель­ным весом , Н/м³ и определяется по формуле

где  - вес жидкости в объеме V.

Удельный вес - величина размерная и измеряется в системе СИ в ньютонах на кубический метр - Н/м3. Например, для воды при температуре t=+4°С  С увеличением температуры удельный вес жидкости уменьшается (исключение – вода).

В справочных материалах приведены значения удельного веса и плотности некоторых жидкостей.

Между плотностью и удельным весом существует связь (меж­ду весом тела G, его массой m и ускорением свободного падения g име­ется зависимость G = mg), которую можно представить в виде

3.Температурное расширение - способность жидкостей изменять объем при изменении температуры. Для капельных жидкостей характе­ризуется коэффициентом температурного расширения , равным отно­сительному изменению объема при изменении температуры t на один градус при постоянном давлении:

где - первоначальный объем; - изменение этого объема при повы­шении температуры на величину

Коэффициент температурного расширения в системе СИ имеет раз­мерность град-1.

Коэффициент  зависит для данной жидкости от температуры и дав­ления.

В некоторых случаях ввиду малости коэффициента температурного расширения изменением плотности жидкости с изменением температу­ры можно пренебречь.

4. Сжимаемость - способность жидкостей уменьшать объем при уве­личении давления. Характеризуется коэффициентом объемного сжатия , который представляет собой относительное изменение объема жид­кости на единицу изменения давления:

где - первоначальный объем жидкости; - приращение (изменение) этого объема при увеличении давления на величину .

Коэффициент объемного сжатия в системе СИ имеет размерность Па-1. Знак минус в этой формуле обусловлен тем, что положительному приращению давления  соответствует отрицательное приращение (т.е. уменьшение) объема жидкости.

Величина, обратная коэффициенту объемного сжатия, называется со­ответственно изотермическим и адиабатическим модулем упругости:

Модуль упругости Е большинства жидкостей настолько велик, что жидкости можно считать практически несжимаемыми. Иногда сжимаемость жидкостей полезна - ее используют в гидравлических амортизаторах и пружинах.

5. Вязкость жидкостей - свойство жидкости сопротивляться относи­тельному движению (сдвигу) ее частиц, обусловливающее появление силы внутреннего трения между слоями жидкости, если последние имеют раз­личные скорости движения.

Это свойство характеризуется коэффициентами динамической и кинематической вязкостей.

Динамическая вязкость  - сила, которая возникает на единице площади поверхности двух движущихся друг относительно друга слоев жидкости при градиенте скорости  = 1 ( -разность скоростей перемещающихся слоев воды, - толщина слоя). В международной системе единиц динамическая вязкость выража­ется в Н-с/м2 или Па-с.

В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости n (м2/с или Стокс). 1 Ст=1 м2/с. Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:

.

Вязкость капельных жидкостей при увеличении температуры умень­шается, а вязкость газов возрастает.
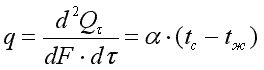