2.Теплопередача через цилиндрическую стенку.

Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d₁и внешним диаметром d₂ (Рис.9.4). 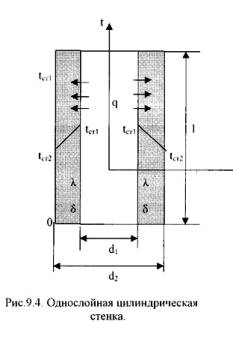Температуры поверхностей стенки –t_ст1 и t_ст2. Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = - λ∙2∙π∙r ·l· ∂t / ∂r (9.24)илиQ = 2·π·λ·l·Δt/ln(d₂/d₁), (9.25)где: Δt = t_ст1 – t_ст2 – температурный напор; λ – κоэффициент теплопроводности стенки. Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:q_l = Q/l =2·π·λ·Δt /ln(d₂/d₁), [Вт/м]. (9.26)Температура тела внутри стенки с координатойd_х:t_x = t_ст1 – (t_ст1 – t_ст2) ·ln(d_x/d₁) / ln(d₂/d₁). (9.27)

3.Вывод чисел подобия (Грасгофа и Нусельта).

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8

1.Понятия о тепловом излучении.

Тепловое излучение представляет собой процесс распространения в пространстве внутренней энергии излучающего тела путем электромагнитных волн. Возбудителями этих волн являются материальные частицы, входящие в состав вещества. Для распространения электромагнитных волн не требуется материальной среды, в вакууме они распространяются со скоростью света и характеризуются длиной волны λ или частотой колебаний ν. При температуре до 1500 ⁰С основная часть энергии соответствует инфракрасному и частично световому излучению (λ=0,7÷50 мкм).

Излучаемая в единицу времени энергия в узком интервале изменения длин волн (от λ до λ+dλ) называется потоком монохроматического излучения Q_λ. Поток излучения, соответствующий всему спектру в пределах от 0 до ∞, называется интегральным, или полным, лучистым потоком Q(Вт). Интегральный лучистый поток, излучаемый с единицы поверхности тела по всем направлениям полусферического пространства, называется плотностью интегрального излучения (Вт/м²)

.

(11.1)

Отсюда

.

Если величина Е одинакова для всех элементов поверхности F, то Q=E·F.

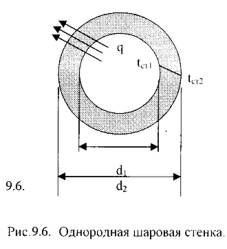
2.Теплопередача через шаровую стенку.

Стационарная теплопроводность через шаровую стенку Пусть имеется полый шар (Рис.9.6) – внутренний диаметр d1, внешний диаметрd2, температура внутренней поверхности стенки –tст1, температуранаружнойповерхности стенки –tст2, коэффициент теплопроводности стенки -λ . Уравнение теплопроводности по закону Фурье в сферических координатах: Q = - λ·4·π·r2· ∂t / ∂r (9.35) Или Q =4·π·λ·Δt/(1/r2 - 1/r1) =2·π·λ·Δt/(1/d1 - 1/d2) = = 2·π·λ·d1·d2·Δt /(d2 - d1) = π·λ·d1·d2·Δt / δ (9.36) где: Δt = tст1 – tст2 – температурный напор; δ –толщина стенки.

3.Уравнение подобия (для жидкости).

При конвективном теплообмене уравнения подобия могут быть представлены в следующем виде:

Nu = f1 (Re, Gr, Pr);(26-44)

Eu = f₂ (Re, Gr, Pr). (26-45)

В случае вынужденного движения жидкости и при развитом турбу­лентном режиме свободная конвекция в сравнении с вынужденной очень мала, поэтому уравнение подобия теплоотдачи упрощается:

Nu = f (Re, Pr).(26-46)

При свободном движении жидкости, когда вынужденная конвек­ция отсутствует, вместо числа Рейнольдса в уравнение подобия теп- лоотдачи необходимо ввести число Грасгофа. Отсюда получаем

Nu = f (Gr, Pr).(26-48)

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9

1.Три теоремы и условия однозначности.

Первая теорема подобия, называемая теоремой Ньютона, утверждает: у подобных явлений однородные параметры и соответственные значения однородных переменных величин связаны между собой посредством равенств одноименных критериев подобия – безразмерных комплексов величин, фигурирующих в безразмерных уравнениях, описывающих эти явления.

Первая теорема подобия утверждает, что для подобных явлений должны существовать одинаковые критерии подобия. Первая теорема не указывает способы установления подобия и способы его реализации, она лишь формирует необходимые условия существования подобия (одинаковые критерии подобия).

Вторая теорема подобия, называемая p – теоремой, утверждает [95]: "Полное уравнение физического процесса, записанное в опреде ленной системе единиц, может быть представлено зависимостью между критериями подобия, то есть зависимостью, связывающей безразмер ные величины, определенным образом полученные из существующих в процессе параметров". Из второй теоремы следует, что если известна функциональная зависимость рассматриваемого явления, то есть известны параметры (факторы), но неизвестно его математическое описание, то можно получить критерии подобия. Вторая теорема так же, как и первая, не указывает способов выявления подобия и способов реализации подобия.

Третья теорема подобия определяет необходимые и достаточные условия подобия физических явлений. Третья теорема подобия утверж дает: "Необходимыми и достаточными условиями для создания подо бия являются пропорциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия изучаемого явления". Условия однозначности – это условия, определяющие индивидуальные особенности исследуемого явления, например, на чальные, граничные или краевые условия. Эти условия не зависят от механизма самого исследуемого явления.

Условия однозначности включают в себя: ◊ геометрические условия, характеризующие форму и размеры тела, в которых протекает процесс; ◊ физические условия, характеризующие физические свойства среды и тела; ◊ временные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени; ◊ граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.

2.Теплопроводность при нестационарном режиме для цилиндра бесконечной длины и шара.

Для цилиндра неограниченной длины дифференциальное уравне­ние теплопроводности удобнее отнести к цилиндрическим координатам.

Внутреннюю энергию находим по формуле:

Q₀=πr²lρcϑ

3. Понятия гомохронности.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 10

1.Понятия класса и группы явлений.

2.Теплопроводность через многослойную цилиндрическую стенку

(стационарный режим). Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5). Температура внутренней поверхности стенки –t_ст1, температуранаружнойповерхности стенки –t_ст2, коэффициенты теплопроводности слоев -λ₁, λ₂, λ₃, диаметры слоев d₁, d₂, d₃, d₄. Тепловые потоки для слоев будут: 1-й слой Q = 2·π· λ₁·l·(t_ст1 – t_сл1)/ ln(d₂/d₁), (9.28) 2-й слой Q = 2·π·λ₂·l·(t_сл1 – t_сл2)/ ln(d₃/d₂), (9.29) 3-й слой Q = 2·π·λ₃·l·(t_сл2 – t_ст2)/ ln(d₄/d₃), (9.30)

Решая полученные уравнения, получаем для теплового потока через многослойную стенку:

Q = 2·π·l·(t_ст1 – t_ст2) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (9.31)

Для линейной плотности теплового потока имеем:

q_l = Q/l = 2·π· (t₁ – t₂) / [ln(d₂/d₁)/λ₁ + ln(d₃/d₂)/λ₂ + ln(d₄/d₃)/λ₃]. (9.32)

Температуру между слоями находим из следующих уравнений:

t_сл1 = t_ст1 – q_l·ln(d₂/d₁) / 2·π·λ₁ . (9.33) t_сл2 = t_сл1 – q_l·ln(d₃/d₂) / 2·π·λ₂ . (9.34)

3.Уровнение подобия (для газа).

При конвективном теплообмене уравнения подобия могут быть представлены в следующем виде:

Nu = f1 (Re, Gr, Pr);(26-44)

Eu = f₂ (Re, Gr, Pr). (26-45)

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11

1.Константы и индикатор подобия.

2.Теплопередача через однослойную стенку.

Рассмотрим однослойную плоскую стенку толщиной d и теплопроводностью l (рис12.1).

 Температура горячей жидкости (среды) t^'_ж, холодной жидкости (среды) t^''_ж. Количество теплоты, переданной от горячей жидкости (среды) к стенке по закону Ньютона-Рихмана имеет вид:

 

Q = a₁ · (t^'_ж – t₁) · F, (12.1)

где a₁ – коэффициент теплоотдачи от горячей среды с температурой t^'_ж к поверхности стенки• с температурой t₁; F – расчетная поверхность плоской стенки. Тепловой поток, переданный через стенку определяется по уравнению:

Q = l/d · (t₁ – t₂) · F. (12.2)

Тепловой поток от второй поверхности стенки к холодной среде определяется по формуле:

Q = б₂ · (t₂ - t^''_ж) · F, (12.3)

где a₂ – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t^''_ж. Решая эти три уравнения получаем:

Q = (t^'_ж – t^''_ж) • F • К, (12.4)

где К = 1 / (1/a₁ + / l + 1/a₂) – коэффициент теплопередачи, (12.5) или

R₀ = 1/К = (1/a₁ + d/l + 1/a₂) – полное термическое сопротивление теплопередачи через однослойную плоскую стенку. (12.6)

1/a₁, 1/a₂ – термические сопротивления теплоотдачи поверхностей стенки; d/l - термическое сопротивление стенки.

3.Дифференциальное уравнение движения вязкой несжимаемой жидкости (Новье-Стокса).

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ 12

1.Режимы течения и пограничный слой.

Режим течения жидкости характеризуется числом Рейнольдса Re. Когда значение Re меньше некоторого критического числа Re_kp, имеет место ламинарное течение жидкости; если Re > Re_kp, режим течения может стать турбулентным.

Течение в пограничном слое

Рис.1.

Режим течения в динамическом пограничном слое зависит от Рейнольдса числа Re и может быть ламинарным или турбулентным. При турбулентном режиме в пограничном слое на некоторое усреднённое движение частиц жидкости в направлении основного потока налагается хаотическое, пульсационное движение отдельных жидких конгломератов. В результате интенсивность переноса количества движения, а также процессов тепло- и массопереноса резко увеличиваются, что приводит к возрастанию коэффициента поверхностного трения, тепло- и массообмена. Значение критического числа Рейнольдса, при котором происходит переход в пограничном слое ламинарного течения в турбулентное, зависит от степени шероховатости обтекаемой поверхности, уровня турбулентности внешнего потока, Маха числа М и некоторых др. факторов. При этом переход ламинарного режима течения в турбулентный с возрастанием Re происходит в пограничном слое не внезапно, а имеется переходная область, где попеременно чередуются ламинарный и турбулентный режимы.

Начало перехода от ламинарного течения к турбулентному обычно связывают с появлением бурных процессов в виде турбулентных пятен и низкочастотных пульсаций большой амплитуды. Однако в настоящее время стало совершенно очевидным, что длинная последовательность физических процессов, приводящая в конечном счете к разрушению ламинарного течения (по крайней мере в случае малой интенсивности внешних возмущений), берет начало намного раньше, а именно в трансформации внешних возмущений различной природы во внешнем потоке в волны пограничного слоя либо в их генерации в самом пограничном слое, происходящей на неровностях обтекаемой поверхности (уступы, шероховатости и т. п.). В соответствии с этим термин «процесс перехода к турбулентности или эквивалентный ему термин «возникновение турбулентности» понимаются в широком смысле как совокупность всех явлений, ответственных за разрушение ламинарного режима течения и образование турбулентного пограничного слоя.