№1. Основные понятия об электрических цепях постоянного тока.

Электрическая цепь - совокупность устройств и объектов образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе (ЭДС), токе и напряжении.

Электрическая цепь постоянного тока - цепь, в которой ток не меняет своего направления (полярность источников ЭДС постоянна).

Электрическая цепь состоит из:

1)Источники питания - элементы, предназначенные для выработки электроэнергии (гальванические элементы, электрические аккумуляторы, генераторы).

2)Электроприемники - элементы, преобразующие электроэнергию в другие виды энергии (механическую, световую, тепловую) - электродвигатели.

3)Элементы, предназначенные для передачи электроэнергии от источников питания к электроприемнику (провода).

Элементы эл-ой цепи делят: 1) активные, в которых индуцируется ЭДС (источники ЭДС, эл-двигатели). 2) пассивные.

Резистор - элемент эл-ой цепи, обладающий электрическим сопротивлением R. Характеризуются вольт-амперной характеристикой - зависимостью напряжения на зажимах элемента от тока в нем. Графическое изображение - прямоугольник.

Линейная эл-ая цепь - цепь, эл-ое сопротивление участков которой не зависит от значений и направлений токов и напряжений в цепи.

Нелинейная электрическая цепь - цепь, эл-ое сопротивление хотя бы одного из участков которой зависит от значений или от направлений токов и напряжений на этом участке.

Эл-ая схема цепи - графическое изображение цепи, содержащее условное обозначние ее элементов и показывающее соединение элементов.

Ветвь - участок эл-ой цепи, на всех участках которого существует один и тот же ток.

Узел - место соединения ветвей. Графически обозначается точкой.

Контур - любой замкнутый путь, проходящий по нескольким ветвям.

В. №2. Законы Кирхгофа.

Первый закон: Отражает принцип непрерывности движения эл-их зарядов. В любой момент времени количество эл-их зарядов направленных к узлу, равно количеству зарядов направленных от узла - эл-ий заряд в узле не накапливается.

Формулировка: Алгебраическая сумма токов в ветвях, сходящихся в узле эл-ой цепи, равна нулю:

Второй закон: В любом контуре эл-ой цепи постоянного тока алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на элементах контура:

, n-число ЭДС в контуре, m-число элементов с сопротивлением R_k.

Для одноконтурной цепи: Алгебраическая сумма напряжений участков любого контура цепи равна нулю: , m-число участков.

В. №3. Режимы работы эл-ой цепи. Энергетические соотношения в цепях постоянного тока.

Режимы работы: Внешняя характеристика источников ЭДС - уравнение, описывающее зависимость напряжения на зажимах источника ЭДС от тока в цепи:

, R_ВТ – внутр-ее сопрот-ие источника ЭДС, .

Режим холостого хода-режим , при котором ток в цепи I=0, что имеет место при разрыве цепи. При холостом ходе напряжение на зажимах источника ЭДС U=E, поэтому вольтметр, включенный в такую цепь, измеряет ЭДС источника. На внешней характеристике точка холостого хода обозначена х.

Номинальный режим имеет место тогда, когда источник ЭДС или другой элемент цепи работает при значениях тока, напряжения и мощности, указанных в паспорте устройства. На внешеней характеристике - точка н.

Режим короткого замыкания - режим, когда сопротивление приемника равно нулю, что соответствует соединению зажимов источника ЭДС между собой. При коротком замыкании ток достигает максимального значения , ограниченного внутренним сопротивлением R_ВТ источника ЭДС, а напряжение на зажимах источника ЭДС U=RI=0. Ток короткого замыкания может достигать больших значений, во много раз превышающих номинальный ток. Режим короткого замыкания является аварийным режимом.

Согласованный режим источника ЭДС и внешней цепи имеет место тогда, когда сопротивление внешней цепи R=R_ВТ. Ток в согласованном режиме: ЭДС E источника уравновешивается 2 равными по значению палениями напряжения, обусловленными сопротивлением внешней цепи и внутренним сопротивлением, U=0,5E. На внешней характеристике - точка с. Режим имеет низкое значение КПД (примерно 0,5), что что обуславливает большие потери мощности и энергии в источнике и сетях. Применяют в цепях с малыми токами (схемы автоматики, электрических измерений, связи), в которых КПД не имеет решающего значения.

Энергетические соотношения: Уравнение баланса мощностей эл-ой цепи: EI=UI+R_ВТI² или P₁= P₂+ P_П, где P₁=EI - мощность источника ЭДС, P₂=UI - мощность энергии, потребляемой электроприемником, P_П= R_ВТI² - мощность потерь энергии в источнике ЭДС.

Мощность потерь энергии в источнике параболически зависит от тока, причем при токе короткого замыкания она имеет максимальное значение:

Мощность электроприемника имеет максимальное значение при согласованном режиме, при I=0,5I_К.

Для КП имеет место след. зависимость:

При номинальном режиме КПД много выше, чем при согласованном. Для большинства промышленных источников электроэнергии при номинальном режиме

, номинальный ток много раз меньше тока короткого замыкания.

В. №4. Разветвленные и неразветвленные линейные электрические цепи с одним источником питания.

Последовательное соединение элементов — это са­мое простое соединение. При таком соединении во всех элементах цепи ток имеет одно и то же значение. Таким способом могут быть соединены или все пассивные эле­менты цепи и тогда цепь будет одноконтурной неразветвленной (рис.), или может быть соединена только часть элементов многоконтурной цепи.

Последовательное соединение линейных элементов.

При последовательном соединении п элементов на­пряжение на зажимах цепи будет равно сумме падений напряжения на п последовательно включенных элемен­тах, т. е. U=U₁ + U₂ + U₃ + ... + U_n, или U = R₁I+ R₂I + R₃I + ... + R_nI = (R₁+ R₂ + R₃ + ... + R_n)I = R_экI, где R_эк= - эквивалентное сопротивление цепи.

Ток в цепи рассчитыва­ют по закону Ома:

Падение напряжения на k-м элементе

Отношение падений напряжения на элементах равно отношению сопротивле­ний этих элементов:

Параллельное соединение элементов — это такое со­единение, при котором ко всем элементам цепи приложе­но одно и то же напряжение. По схеме параллельного соединения могут быть соединены или все пассивные эле­менты цепи (рис.), или только часть их.

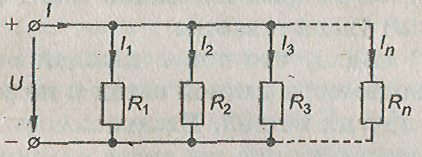
Параллельное соединение линейных элементов.

Каждый параллельно включенный элемент образует отдельную ветвь. Поэтому цепь с параллельным соединением эле­ментов, изображенная на рис., хотя и является про­стой цепью (так как содержит только два узла), в то же время разветвленная. В каждой параллельной ветви ток где G_k=1/R_k – проводимость k–й ветви, G_эк= - эквивалентная проводимость цепи.

При параллельном соединении пас­сивных элементов их эквивалентная проводимость равна сумме проводимостей этих элементов. Эквивалентная проводимость всегда больше проводимости любой части параллельных ветвей. Эквивалентной проводимости G_эк соответствует эквивалентное сопротивление R_эк = 1/G_эк.

Ток в неразветвленной части цепи с параллельным со­единением элементов:

При параллельном соединении ко всем эле­ментам приложено одно и то же напряжение, а ток в каждой ветви пропорционален проводимости этой ветви, то отношение токов в параллельных ветвях равно отно­шению проводимостей этих ветвей или обратно пропор­ционально отношению их сопротивлений:

Смешанное соединение элементов представляет со­бой сочетание последовательного и параллельного соеди­нений. Такая цепь может иметь различное число узлов и ветвей.

Смешанное соединение линейных элементов.

Для расчета такой цепи необходимо последовательно определять эквивалентные сопротивления для тех час­тей схемы, которые представляют собой только последо­вательное или только параллельное соединение.

В. №5. Нелинейные элементы электрической цепи постоянного тока. По виду вольт-амперной характеристики различают нелинейные элементы с симметричной и несимметрич­ной характеристиками (по отношению к началу коор­динат). Значение тока в нелинейном элементе с сим­метричной характеристикой не зависит от полярности приложенного напряжения (рис. а), а сопротивле­ние этого элемента не за­висит от направления тока в нем. В нелинейном эле­менте с несимметричной характеристикой значение тока зависит от полярно­сти приложенного напря­жения (рис. б), а сопро­тивление элемента зависит от направления тока в нем.

Вольт-амперные характеристики нелинейных элементов, а — симметричная; б — несиммет­ричная.

К нелинейным элементам с симметричной характе­ристикой относятся лампы накаливания, терморезисто­ры, тиритовые и вилитовые элементы, бареттеры, лампы с тлеющим разрядом, электрическая дуга между одина­ковыми электродами и др.

Нелинейность характеристик ламп накаливания обус­ловлена тем, что, например, вольфрамовая нить имеет положительный температурный коэффициент сопротив­ления и в соответствии с формулой при повыше­нии температуры (с увеличением тока) ее сопротивле­ние увеличивается и возрастание тока замедляется (1 на рис.). Угольная же нить имеет отрицательный тем­пературный коэффициент сопротивления, и поэтому за­висимость 2 имеет вогнутый характер.

Вольт-амперные характеристи­ки ламп накаливания, 1 — с вольфрамовой питью; 2с угольной нитью.

Терморезистор имеет вольт-амперную характеристи­ку, аналогичную характеристике угольной нити. С увели­чением тока его сопротивление уменьшается. Терморези­сторы применяют для компенсации изменений сопро­тивления элементов, изготовленных из металлических проводников, сопротивление которых увеличивается с увеличением тока в цепи.

Бареттер по внешнему виду напоминает лампу на­каливания. В стеклянном баллоне, заполненном водо­родом, помещается стальная нить. На вольт-амперной характеристике (рис. ) имеется участок АВ, на про­тяжении которого с увеличением напряжения сопротив­ление нити увеличивается так, что ток остается почти постоянным. Бареттер включают последовательно в ту цепь, в которой надо поддержать ток постоянным.

Бареттер, а — вольт-амперная характеристика; б — условное обозначение на элект­рических схемах.

К нелинейным элементам с несимметричной вольт-амперной характеристикой относятся элек­тронные лампы, ртутные венти­ли, полупроводниковые диоды и триоды, электрическая дуга при неоднородных электродах и др. В основном их используют для преобразования переменного тока в постоянный ток.

терми-стора — терморезистора из полу­проводникового материала.

Термистор, а - вольт-амперная характери­стика; б - условное обозначе­ние на электрических схемах.

Электронная лампа (диод) про­водит электрический ток, если анод имеет положительный по­тенциал, а катод — отрицатель­ный. При обратной полярности электродов ток, замыкающийся через лампу, практически равен нулю (рис.).

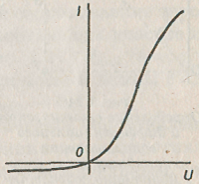
Вольт-амперная характеристика электронной лампы (диода).

Нелинейные элементы харак­теризуются двумя параметрами: статическим R_ст и дифференциаль­ным R_диф сопротивлениями.

Статическое сопротивление нелинейного элемента определя­ется отношением напряжения в данной точке вольт-амперной ха­рактеристики к току в этой же точке. Для точки А характерис­тики (рис. а, б) статическое сопротивление где m_U, m_I, m_R – масштабные коэффициенты для напряжения, тока и сопротивления соответ­ственно.

Определение статического и дифференциального сопротивлений нелинейных элементов с монотонно возрастаю­щей зависимостью между напряжением и током, а — с выпуклой вольт-амперной характеристикой; б — с вогну­той вольт-амперной характери­стикой.

Под дифференциальным со­противлением понимают предел отношения приращения напря­жения в данной точке вольт-ам­перной характеристики к прира­щению медленно изменяющего­ся тока, когда это приращение стремится к нулю. Для точки А характеристики (рис. а, б) дифференциальное сопро­тивление .

В. №6. Получение синусоидальной ЭДС.

Поместим прямоугольную рамку в однородное маг­нитное поле с магнитной индукцией В = const. Площадь рамки S_m — bl, где b — ее ширина, а l — длина. При вращении рамки с постоянной угловой скоростью со сцепленный с нею магнитный поток Ф будет изменяться в зависимости от угла поворота рамки по закону:

где S_a = S_mcosа — площадь рамки, сцепленная с маг­нитным потоком, Ф_т = BS_m - максимальный магнит­ный поток рамки, когда она занимает горизонтальное положение.

Согласно закону электромагнитной индукции в рам­ке будет индуцироваться ЭДС, изменяющаяся по синусо­идальному закону:

где - амплитудное (максимальное) значение ЭДС.

В. №7. Действующие и средние значения синусоидальных ЭДС, напряжения и тока.

Действующим значением синусоидального тока на­зывают такое значение постоянного тока, при кото­ром в одном и том же резисторе с сопротивлением R за время одного периода Т выделяется столько же теплоты, сколько и при синусоидальном токе.

Аналогично, действующие значения ЭДС и напряжений равны соответственно

За среднее значение синусоидального тока принима­ют такое значение постоянного тока, при котором за полпериода переносится такой же электрический заряд, что и при синусоидальном токе.

Аналогично, для ЭДС и напряжения

Отношение действующего значения к сред­нему называется коэффициентом формы периодической кривой.

В. №8. Изображение синусоидальных ЭДС, напряжений и токов в прямоугольных координатах.

В общем случае аргумент синусоидальной функции, называемый фазовым углом или просто фазой, равный или , может отличаться от нуля при t=0. Тогда мгновенные значения можно записать так:

Значение фазового угла при t=0 называют начальной фазой

Синусоидальные напряжение и ток, совпадающие по фазе.

когда начальные фазы рав­ны нулю синусоидальные величины одновременно принимают нулевые или максимальные значения.

Если две синусоидальные величины одновременно проходят через нулевые значения и одновременно при­нимают максимальные значения противоположных зна­ков, то такие величины находятся в противофазе или сдвинуты по фазе на угол (рис.).

Синусоидальные ЭДС и напряжение, находящиеся в противофазе.

На практике чаще всего имеют место случаи, когда ЭДС, напряжения и токи не совпадают по фазе, т. е. через нулевые значения проходят не одновременно (рис.).

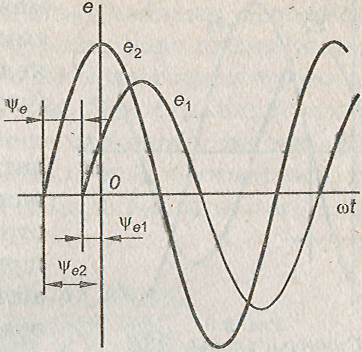
Синусоидальные ЭДС, несовпадающие по фазе.

Если такие ЭДС описываются уравнениями то при ЭДС е₂ опережает по фазе ЭДС е₁, или ЭДС е₁ отстает по фазе от ЭДС е₂. Разность фазовых углов, равную разности начальных фаз называют разностью или сдвигом фаз.

С помощью графического изображения в прямоуголь­ных координатах можно находить опережающую и отста­ющую синусоидальные величины. При этом пользуются таким правилом. Отстает по фазе та из двух синусоидаль­ных величин, которая при переходе от отрицательных зна­чений к положительным позже (правее) пересекает ось аб­сцисс.

В. №9. Векторное изображение синусоидальных ЭДС, напряжений и токов.

Графическое построение синусоидальных величин в прямоугольных координатах является довольно трудоем­кой операцией. Значительно проще складывать две сину­соидальные величины, изменяющиеся с одинаковой час­тотой, представив их вращающимися векторами.

В плоскости с осями координат ОХ и OY (рис. а) рассмотрим вращающийся с постоянной скоростью, рав­ной угловой частоте , вектор ОА, длина которого рав­на амплитуде синусоидальной ЭДС е = E_msin(( ), т. е.

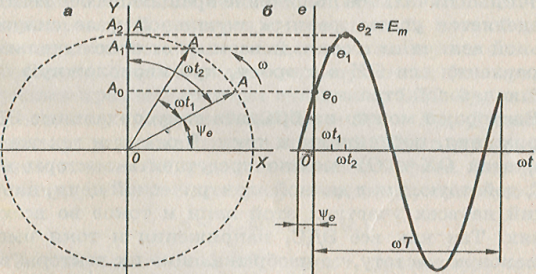
Векторное изображение синусоидальных ЭДС, а — вращающийся вектор; б — кривая изменения его проекции на ось ОY.

За положительное направление вращения вектора ОА принимаем направление, противоположное вращению часовой стрелки, а угол поворота вектора отсчитываем от оси ОХ. В начальном положении (при t = 0) вектор ОА повернут по отношению к оси ОХ на угол .

Построим проекции вектора ОА на ось OY (рис. 6), которые изменяются по мере поворота вектора на угол по отношению к начальному положению. В начальном положении проекция ОA₀ = OAsin = =E_msin =e₀, т. е. равна мгновенному значению ЭДС при t = 0. Через неко­торое время вектор ОА повернется на угол и будет составлять с осью ОХ угол . Проекция его на ось OY: OA₁ = ОА sin =E_msin =е₁, т.е. рав­на мгновенному значению ЭДС при t = t₁. При t = t₂ век­тор ОА направлен по оси OY и его проекция ОА = Е_m = е₂. При дальнейшем вращении вектора ОА его проекции на ось OY начнут уменьшаться, затем станут отрицатель­ными и т. д.

Проекции на ось OY вектора, враща­ющегося с постоянной скоростью и имеющего длину, равную амплитуде ЭДС, изменяются по синусоидально­му закону, т. е. представляют собой мгновенные значе­ния синусоидальной ЭДС. Следовательно, справедливо и обратное: любую синусоидально изменяющуюся во вре­мени величину можно изображать вращающимся векто­ром, длина которого равна амплитуде, а угловая ско­рость вращения — угловой частоте этой синусоидальной величины.

Так как все ЭДС, напряжения и токи имеют одинаковую частоту, то изображающие их векторы вра­щаются с одинаковой угловой скоростью. Их взаимное расположение на плоскости остается постоянным. По­этому векторы на практике не вращают, а строят их, соблюдая углы между векторами, которые представляют собой утлы сдвига фаз.

Совокупность векторов ЭДС, напряже­ний и токов, являющихся изображениями ЭДС, напряжений и токов одинаковой час­тоты, действующих в какой-то электриче­ской цепи, построенных с учетом их пра­вильного взаимного расположения на плос­кости, называют векторной диаграммой.

Начальные фазы напряжения и тока на векторной диаграмме никак не изображаются, так как взаимное положение векторов полностью опре­деляется разностью фаз .

В. №10. Комплексный метод.

Комплексный метод расчета электрических цепей си­нусоидального тока применим только при установивших­ся режимах работы цепей и основан на использовании преобразований:

синусоидальному току i (оригиналу) может быть поставлено в соответствие комплексное чис­ло (изображение) Условная запись такого преобразования имеет вид

Аналогичные преобразования могут быть выполнены для синусоидальных напряжений и ЭДС:

Комплексное число

модуль и аргумент которого соответственно равны амплитуде и начальной фазе синусоидального тока, называют комплексной амплитудой тока.

Комплексным действующим током (комплексным током) называют комплексное число

Аналогично комплексные амплитуды и комплексные действующие напряжения и ЭДС соответственно равны

Сущность комплексного метода заключается в том, что, используя указанные преобразования, систему дифференциальных уравнений для действительных функ­ций времени можно заменить системой алгебраических уравнений с комплексными токами, напряжениями и ЭДС Переход от дифференциальных уравнений к алгебраиче­ским уравнениям с комплексными числами осуществля­ют заменой в них мгновенных значений тока г, напряже­ния и и ЭДС е комплексными числами в соответствии с и , а производых и интегралов от них — комплексными числами в соответствии с

Так как комплексные амплитуды тока, напряжения и ЭДС и комплексные действующие токи, напряжения и ЭДС можно изображать векторами на комплексной плоскости, то расчет электрических цепей полезно сопровождать по­строением векторных диаграмм, под которыми понимают совокупность векторов на комплексной плоскости, изобра­жающих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением пра­вильной их ориентации относительно друг друга по фазе, что в ряде случаев позволяет выявить ошибки расчета. На векторных диаграммах принято изображать векторы комп­лексных токов, напряжений и ЭДС или комплексные ам­плитуды этих величин для момента времени t = 0.

В. №11. Электрические цепи с резистором, индуктивным и емкостным элементами.

Электрическая цепь с резистором.

Электрический ток проводимости в металлах пред­ставляет собой направленное движение свободных элек­тронов, скорость и направление которого определяются значением и полярностью приложенного к проводнику напряжения. При движении электроны сталкиваются с атомами проводящего вещества и кинетическая энер­гия электронов, запасенная ими при ускорении, пре­вращается в тепловую энергию, затрачиваемую на на­грев проводника и рассеиваемую в окружающую среду. Это необратимый активный процесс преобразования электрической энергии, который количественно опре­деляется сопротивлением R. Потому его называют ак­тивным сопротивлением.

Активным сопротивлением обладают практически все материалы, проводящие электрический ток (металлы, уголь, электролиты. Элементы электрической цепи, обладающие только активным сопротивлением R, назы­вают резисторами.

Амплитуда тока в цепи

Так как действующие значения напряжения и тока в V2 раз меньше их макси­мальных значений, то можно записать I = U/R, т. е. действующие значения синусоидальных напряжений и тока связаны между собой законом Ома так же, как постоянные напряжение и ток.

Электрическая цепь с резистором R, а — схема; б — изменение мгно­венных значений тока и напряже­ния.

Электрическая цепь с индуктивным элементом.

Индуктивностью L теоретически обладают все про­водники с током. Но в некоторых случаях эта индуктив­ность так мала, что ею вполне можно пренебречь. Индуктивность возрастает, если созданный током обмотки магнитный поток замыкается по пути с малым магнитным сопро­тивлением (например, по стальному сердечнику), вслед­ствие чего магнитный поток увеличивается.

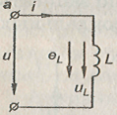
Схема электрической цепи индуктивностью L.

в цепи с индуктивностью ток также изме­няется по синусоидальному закону и отстает по фазе от напряжения на .

Индуктив­ное сопротивление:

Индуктивное сопротивление прямо пропорционально частоте и индуктивности.

- амплитуда тока

Для действующих значений напряжения и тока I = U/X_L.

Электрическая цепь с емкостным элементом.

Элементом электрической цепи, обладающим значи­тельной емкостью, является конденсатор. Конструктив­но конденсатор представляет собой две пластины с боль­шой поверхностью, выполненные из проводящего матери­ала и разделенные диэлектриком. Емкость С конденсатора определяет тот электрический заряд, который накапли­вается на пластинах при разности потенциалов между ними в 1 В.

Схема электрической цепи с емкостью C.

Ток в цепи , где амплитуда тока .

Из формулы видно, что ток в цепи с емкостью является синусоидальным и опережает напряжение по фазе на .

Емкостное сопротивление:

Емкостное сопротивление обратно пропорционально частоте и емкости конденсатора.

Значение тока в цепи с конденсатором I_m=U_m/X_с. Поделив обе части этого уравнения на , получим выражение закона Ома для действую­щих значений тока и напряжения: I = U/X_с.

В. №12.Электрическая цепь при последовательном соединении элементов с R, L и C.

Схема электрической цепи при последовательном соединении элементов с R, L u C.

R, L и С — это параметры электрической цепи, причем активное сопротивление R характеризует активный (не­обратимый) процесс преобразования электрической энергии в другие виды энергии, а индуктивность L и емкость С — обратимый процесс преобразования энер­гии электромагнитного поля.

Действующие значения для последовательного соединения R, L и С:

I=U/Z; U_R=RI; U_L=X_LI;U_C=X_CI.

Сдвиг фаз:

Амплитудное значение тока: .

Значение угла зависит от соотношения между реактивным X и активным R сопротивлениями.

В. №13. Закон Ома в комплексной форме.

Уравнение для комплексных действующих значений на­пряжения и тока :

Эти выражения являются записью закона Ома в комплексной форме. Коэффициент Z в этих формулах называют комплексным электрическим сопротивлением.

, где R= - вещественная составляющая комплекс­ного сопротивления Z, равная активному сопротивлению цепи; X = Х_L – Х_C = — мнимая составляющая комплексного сопротивления Z, называемая реактивным сопротивлением цепи, причем реактивное сопротивле­ние цепи равно алгебраической разности индуктивного и емкостного сопротивлений. Реактивное сопротивление по­ложительно, если X_l > Х_C, и отрицательно, если Х_L < Х_C, Z — полное сопротивление цепи, причем Z=lZl=U/I= .

В. №14. Треугольники напряжений и сопротивлений. Последовательное соединениеие нескольких электроприемников.

Если электрическая цепь состоит из последовательно соединенных элементов с активным и реактивным со­противлениями, то векторная диаграмма напряжений имеет вид прямоугольного треугольника. Гипотенуза этого треугольника равна пол­ному напряжению U на зажимах цепи, а катеты тре­угольника - активной U_а=RI и реактивной U_p состав­ляющим этого напряжения, причем U_p=U_L-U_C=(X_L-X_C)I=XI.

U_а =Ucos ;U_р =Usin ,

где ;

После деления всех сто­рон треугольника напряже­ний на ток I получим тре­угольник сопротивлений, по­добный треугольнику напря­жений,

Треугольники сопротивлений, а — при X_L > Х_С; б - при X_L < Х_C.

стороны которого равны:

U_а/I=R; U_р/I=X; U/I=Z/

R=Zcos ; X=Zsin ; ;

=arctgX/R.

Последовательное соединение нескольких электроприемников.

Рассмотрим электрическую схему цепи с последова­тельным соединением нескольких приемников электри­ческой энергии (электроприемников), у каждого из кото­рых известно как активное, так и реактивное сопротив­ления.

Полные сопротивления элементов:

Z₁=R₁, , , .

Схема последовательного соединения нескольких электроприемников.

R=R₁+R₂+R₃+R₄, .

Действующее значение тока — сдвиг фаз между током и напряжением на за­жимах цепи: I=U/Z; .

Действующее значение активной составляющей напря­жения на зажимах цепи: .

Реактивная составляющая напряжения:

.

В. №15. Мощность цепи синусоидального тока.

Мгновенное значение мощности цепи синусоидально­го тока равно произведению мгновенных значений на­пряжения и тока:

р = ui.

мгновенное значение мощности имеет две составляющие: постоянную UIcos , не изменяющую­ся во времени, и переменную UIcos(2 - ), изменяющуюся периодически с частотой 2 .

Средняя мощность характеризует интенсивность передачи электроэнергии от источника к приемнику и ее преобразования в другие виды энергии, т. е. активный необратимый процесс.

Поэтому среднюю мощность называют активной мощ­ностью P=UIcos и измеряют в ваттах (Вт) киловаттах (кВт) и мегаваттах (МВт).

Интенсивность обмена электроэнергией характеризуется реактивной мощно­стью Q_L, равной амплитуде мгновенного значения мощ­ности, т. е. Q_L=UI.

Реактивную мощность измеряют в вольт-амперах ре­активных (В*Ар), киловольт-амперах реактивных (кВ*Ар) и т. д.

Полную мощность выражают в вольт-амперах (В*А), киловольт-амперах (кВ*А) и т. д. Ее можно вычислять по формулам

,

где Y =1/Z — полная проводимость цепи.

Соотношение между полной, активной и реактивной мощностями:

Коэффициент мощности:

Он показывает, какая доля полной мощности составляет активную мощность или какая доля всей электроэнер­гии преобразуется в другие виды энергии.

Коэффициент мощности - важный эксплуатацион­ный параметр электроприемников. Так как , то чем выше , тем при меньшем значении тока в цепи может быть произведено преобразование электроэнергии в другие виды энергии. Это приводит к уменьшению потерь электроэнергии, ее экономии и удешевлению устройств электропередачи.

В. №16. Электрическая цепь при параллельном соединении элементов с R, L и C.

При анализе процессов в электрической цепи с па­раллельным соединением элементов, обладающих актив­ным сопротивлением R, индуктивностью L и емкостью С, к которой приложено синусоидальное напряжение воспользуемся комплексным методом.

- активная, индуктивная и емкостная проводимости.

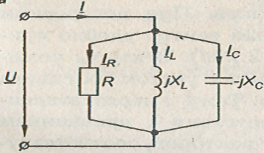
Схема цепи параллельного соединения элементов с R, L и С.

- полная электрическая про­водимость цепи.

- реактивная проводимость цепи.

- сдвиг фаз между напряжением U и током I.

Активная, реактивная и полная мощности цепи

реактивная мощность отдельных ветвей и

В. №17.Соотношения между эквивалентными параметрами цепи при последовательном и параллельном соединении элементов.

Большинство электроприемников переменного тока характеризуются как активной, так и реактивной мощ­ностью.

Схема электрической цепи, эквивалентная данному электроприемнику, может состоять либо из последова­тельного соединения элементов с активным и реактив­ным сопротивлениями (рис. а), либо из параллель­ного соединения элементов с активной и реактивной про­водимостью (рис. 6).

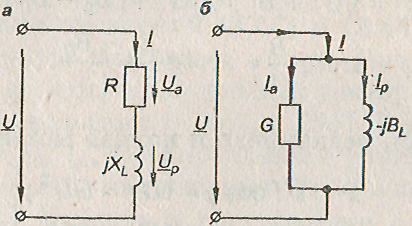
Эквивалентные схемы электроприемника, а — в виде последовательного соединения элементов; б — в виде параллельного соединения элементов;

При расчете электрических цепей может оказаться целесообразной замена последовательного соединения активного и реактивного элементов схемы цепи парал­лельным их соединением или наоборот.

Если необходимо заменить последовательное соедине­ние элементов параллельным соединением элементов, то для этого нужно воспользоваться соотношениями:

,

где - полное электрическое сопротивление цепи.

При переходе от параллельного соединения элементов к последовательному соединению поступают аналогично, при этом связь между параметрами будет иметь вид

,

где - полная электрическая проводимость цепи.

В. №18. Резонанс напряжений в электрических цепях синусоидального переменного тока.

Резонанс — явление в электрической цепи (или на ее участке), содержащей индуктивные и емкостные элемен­ты (хотя бы по одному), возникающее в случае, когда реактивное сопротивление или реактивная проводимость этой цепи (или ее участка) равны нулю.

При резонансе в цепи (или на ее участке) напряжение и ток совпадают по фазе, а реактивная мощность равна нулю.

Различают резонанс напряжений при последовательном и резонанс токов при параллельном соединении R, L и С.

При последовательном соеди­нении элементов с R, L и С (рис.) ток в цепи

Схема электрической цепи при последовательном соединении элементов с R, L u C.

Из всех возможных соотношений между индуктив­ным X_L и емкостным Х_C сопротивлениями особый инте­рес представляет случай, когда эти сопротивления рав­ны, т. е. Х_L = Х_C. В этом случае реактивное сопротивле­ние цепи X=X_L-Х_C=0 и полное сопротивление Z=R минимально. Тогда ток в цепи I = U/R и при U=const, R=const значение его максимально.

Напряжения на индуктивном и емкостном элементах в комплексной форме U_L=-U_C,а действующие значе­ния равны, т. к. U_L=X_LI=X_CI=U_C. Следовательно,

Режим цепи при по­следовательном соединении эле­ментов с R, L и С, когда X_L = Х_С, а напряжения на индуктивном U_L. и емкостном U_C элементах, находящиеся в противофазе, равны по значению и могут пре­вышать напряжение всей цепи, носит название резонанса напряжений.

Активная мощность такой цепи a реактивная . Реактивные же мощности ин­дуктивной катушки и конденсатора не равны нулю: их мгновенные значения в любой мо­мент времени равны между собой, но противоположны по знаку. Происходит непрерывный обмен энергией меж­ду магнитным полем катушки и электрическим полем конденсатора.

В. №19. Резонанс токов в электрических цепях синусоидального переменного тока.

В электрической цепи при параллель­ном соединении ветвей с R (G), L (B_L) и С (В_С) (рис.) ток определяют по формуле:

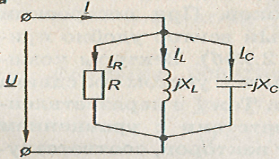
Схема цепи параллельного соединения элементов с R, L и С.

Особый интерес представляет случай, когда индук­тивная и емкостная реактивные проводимости равны друг другу. Тогда полная проводимость цепи Y=G, так как В=B_L–B_С=0, а ток в неразветвленной части цепи I=GU имеет минимальное значение и только активную состав­ляющую I=I_а.т Следовательно, cos =1.

Токи в ветвях с проводимостями B_L и В_С с учетом :

т. е. равны по значению (I_L=I_С) и могут превышать ток I в цепи в B_L/G раз, если B_L = Bc>G.

Режим цепи при параллельном соединении элемен­тов с R, L и С, когда B_L = В_С, а токи I_L и I_С в ветвях с реактивными проводимостями равны по значению и мо­гут превышать ток I цепи, называют резонансом токов. Для этого режима характерно: I_L= I_С>I, если B_L = В_С>G; I= I_min, =0, cos =1; P=UIcos =UI=S, Q_L=B_LU²>0, Q_C=B_CU²>0,Q=Q_L-Q_C=0.

В. №20. Повышение коэффициента мощности.

Активная составляющая тока определя­ет преобразование электроэнергии в другие виды энер­гии, т. е. позволяет количественно оценить совершае­мую работу. Реактивная же составляющая тока никакой работы не производит. Однако при ее наличии увеличи­вается полный ток.

Для обеспечения заданного значения коэффициента мощности предприятия необходимо устанавливать кон­денсаторы определенной мощности или емкости. Если электроприемники имеют мощность Р = const и cos , то их реактивная индуктивная мощность . При заданном значении , которое должно обеспечить предприятие , реактивная мощность элек­троприемников, обеспечиваемая источником питания, .

Разность реактивных мощностей Q₁ - Q₂ компенси­руется емкостной реактивной мощностью конденсаторов

Q_С = Q₁ – Q₂ = P(tg ₁ - tg ₂). (2.6.4)

Реактивную мощность конденсаторов можно также определить по формуле .

Приравнивая правые части этих уравнений, получим .

При этом емкость измеряется в фарадах, если мощ­ность измерена в ваттах, а напряжение — в вольтах.

Для полной компенсации ( ₂=0) необходимо, чтобы .

В. №21. Расчет Линейных Электрических Цепей (ЛЭЦ) методом контурных токов.

Под контурным током понимают условный (вообра­жаемый) ток, замыкающийся только по своему контуру (при этом рассматривают только независимые контуры). Для независимых контуров запи­сывают систему уравнений по второму закону Кирхгофа, в результате решения которой находят эти токи.

Для написания уравнений по второму закону Кирх­гофа поступают следующим образом:

1. Задают условные положительные направления кон­турных токов, причем в качестве независимых конту­ров удобнее выбирать контуры с наименьшим числом ветвей.

2. Направление обхода контура выбирают совпадаю­щим с направлением контурного тока.

3. Суммируют все ЭДС в контуре, причем если на­правление ЭДС совпадает с направлением обхода конту­ра, то ЭДС считают положительной, и наоборот.

4. Суммируют падения напряжения на всех элементах рассматриваемого контура, обусловленные данным кон­турным током, а также обусловленные другими контур­ными токами в элементах этого контура.

для любой цепи система п линейных алгебраи­ческих уравнений для п контурных токов,обозначенных будет иметь вид :

Для конкретной электрической цепи слагаемые в левой части системы уравнений будут равны нулю, если контуры k и m не имеют общих ветвей. Перед слагае­мыми, которые войдут в уравнение, необходимо ставить знак плюс или минус в зависимости от направления тока и направления обхода контура.

Решая систему уравнений относительно контур­ных токов, находим ток в контуре k: , здесь - главный комплексный определитель системы.

Причем взаимные сопротивления берут с тем знаком, какой они имеют в системе уравнений; - определитель, получаемый из главного определителя путем замены k-го столбца правой частью системы урав­нений.

В. №22. Понятие трехфазной системе электрических цепей. Получение трехфазной системы ЭДС.

Трехфазная система электрических цепей представ­ляет собой совокупность электрических цепей, в которых действуют три синусоидальные ЭДС од­ной и той же частоты, сдвинутые друг относи­тельно друга по фазе и создаваемые общим источ­ником энергии.

Если все три ЭДС равны по значению и сдвинуты по фазе на 120° по отношению друг к другу, то такую систему ЭДС называют симметричной (рис. а). Если ЭДС не равны по значению (рис. б) или сдвинуты друг относи­тельно друга на угол, не равный 120° (рис. в), то такую систему ЭДС называют несимметричной. Аналогично оп­ределяются трехфазные системы напряжений и токов.

Трехфазная система ЭДС, а — симметричная; б-несимметричные.

Часть трехфазной системы электрических цепей, в которой существует один из токов трехфазной системы, называют фазой. Фазой являются обмот­ка генератора, в которой индуцируется ЭДС, и прием­ник, присоединенный к этой обмотке.

Получение трехфазной системы ЭДС.

Трехфазная система ЭДС создается трехфазными ге­нераторами. В неподвижной части генератора (статоре) размещают три обмотки, сдвинутые в пространстве на 120° (рис.). Это фазные обмотки, или фазы, которые обозначают А, В и С. Этими же буквами обозначают на­чала обмоток фаз генератора. Концы обмоток обознача­ют соответственно X, Y и Z.

Принципиальная схема трехфазного генератора. На вращающейся час­ти генератора (роторе) располагают обмотку возбужде­ния, которую подключают к источнику постоянного тока. Ток обмотки возбуждения создает магнитный поток Ф₀, постоянный (неподвижный) относительно ротора, но вра­щающийся вместе с ним с частотой п. Вращение ротора осуществляется каким-либо двигателем.

Магнитная индукция В поля в воздушном зазоре меж­ду статором и ротором распределена в пространстве по синусоидальному закону, что достигается специальными конструктивными приемами. При вращении ротора вместе с ним вращается и магнитное поле, магнитные силовые линии которого пересекают проводни­ки фазных обмоток статора и согласно закону электромаг­нитной индукции индуцируют в них ЭДС.

ЭДС в каждой последующей фазе бу­дет отставать от ЭДС в предыдущей фазе на 1/3 периода, т. е. на угол . Если принять, что для фазы А началь­ная фаза равна нулю, то ЭДС фазы А а ЭДС фаз В и С соответственно

В. №23. Соединение обмоток генератора и фаз приемника звездой.

ЭДС любой обмотки генератора представляет собой разность потенциалов начала и конца этой обмотки. При этом потенциал одной какой-либо точки (или начала, или конца обмотки) можно считать равным нулю. Тогда комплексный потенциал другой точки будет иметь точно определенное значение.

Принимая равными потенциалы точек, соответству­ющих концам X, Y и Z обмоток фаз генератора, можно объединить их в одну точку N (рис.). Концы фаз при­емников (Z_a, Z_b, и Z_c) также соединяем в одну точку п. Такое соединение обмоток генератора называют соедине­нием звездой (Y). Звездой можно соединять также фазы приемника. Точки N и п называют нейтральными, а провод, соединяющий точку N генератора с точкой п приемника, — нейтральным. Провода А-а, В-b и С-с, соединяющие начала фаз генератора и приемника, назы­вают линейными. На электрических схемах линейные провода принято обозначать латинскими буквами L₁, L₂ и L₃ соответственно, а нейтральный провод — буквой N.

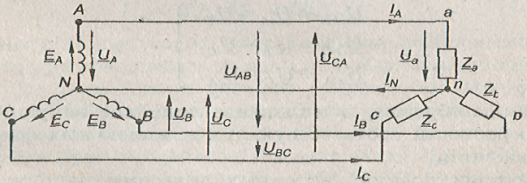
Схема трехфазной несвязанной электрической цепи.

Напряжение между началом и концом фазы — фаз­ное напряжение U_ф. Таким образом, имеется три фазных напряжения — U_A, U_B и U_C. Обычно за условное поло­жительное направление ЭДС генератора принимают на­правление от конца к началу фазы (рис.). Положительное направление тока в фазах совпадает с положительным направлением ЭДС, а положительное направление падения напряжения (напряжение) на фазе приемника совпадает с положительным направлением тока в фазе. Положительным направлением напряжения на фазе генератора, как и на фазе приемника, является направление от начала фазы к ее концу, т. е. противопо­ложное положительному направлению ЭДС.

Напряжение между линейными проводами — линей­ное напряжение U_л. Таким образом, имеется три линей­ных напряжения U_AB, U_BC и U_CA, условные положитель­ные направления которых приняты от точек, соответ­ствующих первому индексу, к точкам, соответствующим второму индексу.

На векторной диаграмме напряжений векто­ры фазных напряжений образуют звезду, а векторы ли­нейных напряжений — замкнутый треугольник, откуда следует, что сумма комплексных линейных напряжений всегда равна нулю, т. е. U_AB+ U_BC + U_CA=0.

Ток в фазах генератора или приемника называют фазным током I_ф. Ток в линейных проводах называют линейным током I_л. Так как обмотка генератора, линей­ный провод и приемник, принадлежащие одной фазе, соединяются последовательно, то при соединении звез­дой линейный ток равен фазному: I_ф= I_л.

В. №24. Соединение обмоток генератора и фаз приемника треугольником.

Соединение обмоток генератора или фаз приемника, при котором начало одной фазы соединяют с концом дру­гой, образуя замкнутый контур, называют соединением треугольником .

Схема трехпроводпой трехфазной цепи

при соединении фаз треугольником.

Условное положительное направление фазных токов приемника принято от точки первого индекса к точке второго индекса. Условное положительное направление фазных напряжений U_ab, U_bc и U_ca совпадает с положи­тельным направлением фазных токов. Условное положи­тельное направление линейных токов I_A, I_B и I_C принято задавать от источника питания к приемнику.

При отключенном приемнике, когда токи I_A, I_B и I_C равны нулю, в замкнутом контуре обмоток источника питания ток равен нулю, так как система ЭДС симмет­рична и суммарная ЭДС в контуре равна нулю (е_A+е_B+е_C= 0).

Напряжение между началом и концом фазы при со­единении треугольником — это напряжение между ли­нейными проводами. Поэтому при соединении треуголь­ником линейное напряжение равно фазному напряжению: U_ф= U_л

Фазные токи определяют по закону Ома: ,

где - действующее значение фазного тока, - аргумент этого тока (его начальная фаза), - сдвиг фаз между напряжением U_ab и током I_ab.

На векторной диаграмме система линейных (фазных) напряжений U_ab, U_bc и U_ca при соединении треугольником образует такой же замкнутый треугольник, как и при со­единении звездой (рис. 4.13). Фазные токи I_ab, I_bс и 1_са при симметричной нагрузке равны по значению и сдвинуты по отношению к векторам напряжений на одинаковый угол ф.

Векторная диаграмма напряжений и фазных токов при соединении фаз треугольником.

В. №25. Напряжение между нейтральными точками генератора и приемника.

Рассмотрим трехфазную цепь при соединении обмо­ток генератора и фаз приемника звездой (рис.). В обмотках генератора индуцируется симметричная си­стема ЭДС. Пренебрегая потерями напряжения в обмот­ках, можно считать, что системы фазных U_A, U_B и U_C и линейных U_AB, U_BC и U_CA напряжений генератора сим­метричны и неизменны. Сопротивления линейных про­водов примем равными нулю. Тогда система линейных напряжений U_ab, U_bc и U_ca приемника будет совпадать с системой линейных напряжений генератора.

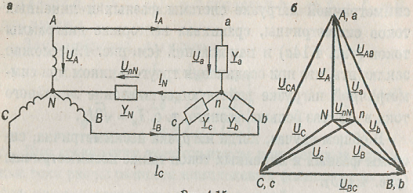
Трехфазная цепь с нейтральным проводом а — схема; б — векторная диаграмма напряжений.

Электрическая цепь состоит из параллельных ветвей с источниками ЭДС и одной параллельной ветви (нейт­ральный провод) с пассивным элементом. Напряжение на этой ветви с учетом :

Потенциал точки N равен нулю, и начало осей комп­лексной плоскости совпадает с этой точкой на векторной диаграмме фазных напряжений генератора. Векторы фаз­ных напряжений U_A, U_B и U_C направлены от точки N к точкам А, В и С. Потенциалам этих точек на схеме (рис). соответствуют комплексные напряжения U_A, U_B и U_C.

При известных проводимостях фаз приемника и ней­трального провода по формуле (последняя формула) можно найти напря­жение U_nN между точками N и n. Вектор напряжения U_nN будет направлен из точки N векторной диаграммы, при­чем его концу будет соответствовать потенциал точки п приемника. Фазное напряжение U_а приемника — это напряжение между точками а и п.

В. №26. Трехфазная цепь с несимметричным приемником.

Соединение фаз приемника звездой с нейтральным проводом. Рассмотрим схему соединения фаз приемника, представленную на рис. Сопротивление нейтрального провода, как и линейных проводов, примем равным нулю (Y_N= ). Как следует из формулы , при этом условии U_nN=0 и система фазных напряжений приемника остает­ся симметричной и неизменной при любых проводимостях фаз приемника. Ток в нейт­ральном проводе определяет­ся фазными токами по фор­муле

Схема соединения фаз приемника звездой с нейтральным проводом.

При наличии нейтрального провода фазные напря­жения приемника остаются постоянными при любых на­грузках фаз и ток каждой фазы зависит только от прово­димости данной фазы. Таким образом, нейтральный про­вод выравнивает фазные напряжения приемника.

Соединение фаз приемника звездой без нейтрального провода. Схема такого соединения фаз приемника нагруз­ки представлена на рис. При отсутствии нейтрально­го провода нужно принять Y_N =0. Тогда напряжение между точками N и п

Схема соединения фаз приемника звездой с нейтральным проводом.

Изменение проводимости одной или несколь­ких фаз приведет к появле­нию напряжения U_nN между нейтральными точками ис­точника питания и приемни­ка й изменению фазных на­пряжений U_a, U_b и U_c,а сле­довательно, и токов в фазах. Так как при отсутствии ней­трального провода и неравен­стве проводимостей (сопро­тивлений) фаз приемника фазные напряжения U_a, U_b и U_c могут значительно откло­няться от номинального зна­чения, соединение фаз при­емника звездой без нейтраль­ного провода никогда не применяют, если заведомо из­вестно, что нагрузка по фа­зам будет несимметричной.

Соединение фаз приемника треугольником. Присо­единении треугольником фазное и линейное напряже­ния равны. Поэтому при заданных неизменных линей­ных напряжениях фазные напряжения на зажимах при­емника останутся постоянными при любом сопротивлении фаз. Векторная диаграмма токов для общего случая не­симметричной нагрузки приведена на рис.

Векторная диаграмма фазныхи линейных токов при соединениифаз треугольником при несимметричной нагрузке.

На практике несимметричные режимы, обусловлен­ные приемником, могут быть следствием нарушения его нормальной работы.

В. №27. Мощность трехфазной системы.

В трехфазной цепи полную, активную и реактивную фазные мощности определяют, как и в однофазных цепях:

где - сопряженный комплексный фазный ток.

Мощность трехфазного приемника или источника равна сумме фазных мощностей:

При симметричной системе напряжений и симметрич­ной нагрузке фазные мощности равны, поэтому мощность трехфазной цепи равна утроенному значению фазной мощ­ности. Мощность трехфазного приемника всегда удобнее вычислять через линейные напряжение и ток, так как линейные величины всегда легче измерять. Принимая во внимание, что при соединении фаз приемника звездой , а при соединении треугольником , формулы для расчета мощности име­ют вид

при неизменном линейном напряже­нии, переключая приемник со звезды в треугольник, его мощность увеличивают в три раза:

В. №28. Основные понятия и принципы анализа переходных процессов.

токи устанавливаются лишь через некоторое время после включения цепи или после изменения ее параметров и могут существовать все время, пока к ней приложено напряжение и параметры остаются неизмен­ными. Эти токи называют установившимися токами, а соответствующие напряжения на отдельных участках цепи — установившимися напряжениями.

Каждому установившемуся режиму электрической цепи соответствует строго определенное энергетическое состояние, т. е. определенные значения энергии элект­рического поля конденсатора и магнитного поля индук­тивной катушки:

.

Любое изменение состояния электрической цепи (вклю­чение, отключение, изменение параметров цепи и т. п.) называют коммутацией.

первый закон коммутации:

ток в цепи с индуктивностью не может измениться скачком.

Согласно второму закону коммутации:

напряжение на зажимах конденсатора или другого емкостного элемента не может измениться скачком.

Индуктивные и емкостные элементы являются инер­ционными, вследствие чего для изменения энергетиче­ского состояния электрической цепи требуется некото­рый промежуток времени, в течение которого происходит переходный процесс. Длительность переходного процес­са, как будет показано далее, зависит от параметров цепи. Хотя такой процесс обычно длится несколько секунд или даже доли секунды, токи и напряжения в это время на отдельных участках цепи могут достигать больших зна­чений, иногда опасных для электроустановок.

Режим цепи синусоидального; тока при после­довательном соединении R, L и С и напряжении источ­ника питания и= U_msin описывается уравнением

Полное решение такого неоднородного линейного диф­ференциального уравнения с постоянными коэффициен­тами ищут в виде

где i’ — частное решение данного неоднородного уравне­ния; i" — общее решение однородного дифференциаль­ного уравнения.

Ток i’ поддерживается в цепи напряжением источ­ника питания и является установившимся током.

Ток i" называется свободным, так как его определя­ют в свободном режиме цепи.

Таким образом» полное решение дифференциально­го' уравнения позволяет определить ток i в цепи в пере­ходном режиме или напряжение на элементах цепи и = и' + и".

В. №29. Основные понятия о несинусоидальных ЭДС, напряжениях и токах.

Периодическая несинусоидальная функция удовлетворяет усло­вию f(t) = f(t + kT), где Т— период функции, т.е. промежуток вре­мени, по истечении которого весь процесс повторяется сначала; k — целое число.

Такая периодическая функция, как известно из курса математи­ки, может быть представлена в виде гармонического ряда (ряда Фу­рье), в общем случае неограниченного, но при расчетах электричес­ких цепей часто с конечным числом п гармонических (синусоидаль­ных) составляющих или, короче, гармоник. Например, несинусои­дальный периодический ток

или

В этом выражении I₀ — постоянная составляющая (постоянный ток); — первая (основная) гармоника, частота кото­рой равна частоте несинусоидальной периодической функции — тока i; все остальные слагаемые называют высшими гармониками; - начальная фаза k-й гармонической составляющей, зависящая от начала отсчета времени (t=0). Таким образом, периодический несинусоидальный ток можно представить в виде суммы постоян­ного тока и синусоидальных токов различных частот, кратных час­тоте первой гармоники, с различными начальными фазами. Такое представление часто применяется при расчетах цепей периодичес­ких несинусоидальных токов.

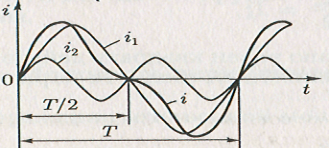
На рис. приведен график периодического несинусоидального тока i, который содержит только первую i₁ и вторую i₂ гармоники. Аналогично записываются разложения в гармонический ряд периодических несинусоидальных напряжений на любом участке цепи:

ЭДС источник

В. №30. Назначение, устройство и принцип действия трансформаторов.

Трансформатором называют статическое устрой­ство, имеющее две или большее число индуктивно связанных обмоток и предназначенное для преобра­зования посредством электромагнитной индукции одной или нескольких систем переменного тока в одну или несколько других систем переменного тока.

Трансформаторы применяют в установках электросвар­ки (сварочные трансформаторы), в металлургической про­мышленности (электропечные трансформаторы), в полу­проводниковых преобразователях, с помощью которых осу­ществляют выпрямление переменного тока в постоянный и наоборот (выпрямительные трансформаторы), в системах измерения (измерительные трансформаторы), в радио- и те­леустановках, в системах автоматического управления, связи и др.

Основными элементами любого трансформатора явля­ются стальной магнитопровод и обмотки. Магнитопровод служит для размещения на нем обмоток и усиления индуктивной: связи между обмотками.. По­скольку магнитная проницаемость магнитоировода в сот­ни раз превышает магнитную проницаемость воздуха, то магнитный поток, создаваемый токами в обмотках транс­форматора, будет замыкаться в основном по магнитопро-воду, что позволяет увеличить магнитный поток при про­чих равных условиях и, следовательно, усилить индук­тивную связь обмоток.

В зависимости от количества N обмоток трансформа­торы бывают двухобмоточными (N=2), трехобмоточ­ными (N=3) и многообмоточными (N>3).

Первичной обмоткой трансформатора называют об­мотку, к которой подводят электрическую энергию, а вторичной — обмотку, к которой подключают прием­ник электрической энергии.

Обмотку, рассчитанную на более высокое напряже­ние, называют обмоткой высшего напряжения (ВН), а рассчитанную на более низкое напряжение — обмоткой низшего напряжения (НН). Выводы обмотки ВН одно­фазного трансформатора обозначают прописными латин­скими буквами А и X, а обмотки НН — строчными ла­тинскими буквами а и х.

Принцип действия трансформатора основан на явле­нии электромагнитной индукции. Так, если к первич­ной обмотке подвести переменное напряжение и₁, то в ней появится переменный ток i₁. Ток i₁ создает пере­менную магнитодвижущую силу (МДС) i₁ которая, в свою очередь, создает переменный магнитный поток Ф, замыкающийся в основном по стальному магнитопроводу. Этот магнитный поток называют основным магнит­ным потоком. Основной магнитный поток сцепляется со всеми витками как первичной, так и вторичной об­моток трансформатора и, согласно закону электромаг­нитной индукции, индуцирует в них переменные ЭДС е₁ и е₂ соответственно. Если теперь к зажимам вторич­ной обмотки подключить приемник электроэнергии, то под действием ЭДС е₂ в приемнике возникнет перемен­ный ток i₂.

Действующие значения первичной и вторичной ЭДС:

Отношение первичной ЭДС к вторичной, равное отно­шению чисел витков обмоток, называют коэффициентом трансформации трансформатора

Если необходимо повысить напряжение источника питания, то число витков вторичной обмотки делают боль­ше числа витков первичной обмотки . Такой трансформатор называют повышающим. Если это напря­жение надо понизить, то делают . В этом случае трансформатор будет понижающим. Если требуется не­сколько различных значений вторичного напряжения, то на тот же магнитопровод наматывают несколько вто­ричных обмоток с различным числом витков.

При подключении первичной обмотки трансформатора к источнику переменного тока на зажимах вторичной обмотки индуцируется переменная ЭДС и вторичная обмотка становится источником питания, к которой можно присоединить какой-либо электроприемник.

Билет 31. Уравнение напряжений трансформатора.

МДС первичной и вторичной обмоток создают так называемые потоки рассеяния Ф1_рас И Ф2_рас, каждый из которых сцеплен только c той из обмоток, МДС которой он создан. Магнитные силовые линии потоков рассеяния замыкают­ся преимущественно по возду­ху, поэтому индуктивности L₁ первичной и L₂ вторичной об­моток, обусловленные этими потоками, можно считать постоянными. Если токи в обмотках изменяются во времени по сину­соидальному закону, т. e. , и то потоки рассеяния также будут изменяться во времени, и в обмотках трансформатора при этом будут индуцироваться ЭДС самоиндукции, называемые ЭДС рассеяния:

Где и - амплитудные значе­ния этих ЭДС, а и

индуктивные сопротивления первичной и вторичтой обмо­ток соответственно, обусловленпые потоками рассеяния.

Действующие значения ЭДС рассеяния

Электрические схемы обмоток трансформатора. Здесь R₁ и R₂ – активные сопротивления обмоток, - комплексное сопротивление электроприемника, а вертикальная линия между обмотками означаeт что обмотки расположены на одном магнитопроводе.

На основании второго закона Кирхгофа с учетом уравнений можно написать урав­нения напряжений для первичной и вторичной обмоток трансформатора в комплексной форме.

Где и - комплексные сопро­тивления первичной и вторичной обмоток.

Билет 32 Холостой ход трансформатора.

Холостым ходом трансформатора называют режим, когда его вторичная обмотка разомкнута, ток в ней I₂ = 0 (нагрузка отсутствует). В режиме холостого хода к пер­вичной обмотке подведено напряжение u₁, в ней существует ток холостого хода i₀, а по магнитопроводу замыкается магнитный поток Ф, индуцирующий в первичной обмотке ЭДС е₁ и во вторичной – е₂.

Маг­нитный поток изменяется во времени по синусоидально­му закону. Изменение во времени тока i₀, создающего этот поток, и самого потока Ф определяется петлей гистерезиса. Восходящая ветвь соответствует четверти периода, когда магнитный поток увеличивается, а нисходящая - четверти периода, ког­да магнитный поток уменьшается. На рис. 7.11в показана зависимость тока холостого хода i₀ = f(t) в течение полупериода, найденная графи­ческим путем.

Как видно из рис. 7.11, ток холостого хода несинусо­идален. На практике при расчетах трансформатора и ана­лизе его работы несинусоидальный ток холостого хода за­меняют эквивалентным синусоидальным током (рис. 7.12а), амплитудное значение которого равно , где действующее значение тока i₀. Эквива­лентный синусоидальный ток опережает по фазе синусои­дальный магнитный поток на угол δ_с. Из векторной диаграммы видно, что комплексный ток холостого хода Iо кроме индуктивной составляющей I_μ , совпадающей по фазе с магнитным потоком и называе­мой намагничивающим током, имеет активную состав­ляющую I_оа совпадающую по фазе с напряжением U₁. Эта составляющая тока определяет ту часть электроэнер­гии, которая преобразуется в тепловую энергию преимущественно в магнитопроводе вследствие явления гисте­резиса и возникновения вихревых токов в нем при его перемагничивании переменным магнитным потоком. При этом вся тепловая энергия затрачивается на нагрев маг­нитопровода. Потери мощности холостого хода, затрачиваемые на нагрев магнитопровода . Для определения тока холостого хода I_o и потерь мощности Р_п0 проводят опыт холостого хода.

Опыт холостого хода. Для проведение опыта xoлoc­того хода собирают злектрическую цепь, схема которой изобряжена на рис. 7.13. Подводимое к первичной об­мотке напряжение U₁ измеряют от 0 до 1,1U_1ном, с помо­щью регулятора напряжения или автотрансформатора. Вторичная обмотка трансформатора разомкнута, к ее зажимам присоединен вольтметр V2 для измереиия напряжения U2. Измеряют напряжения U₁ и U₂, ток холостого хода Io и активную мощность Р₀ энергии, потребляемой трансформатором в режиме холостого хода. По данным измерений строят зависимости I₀ и P₀ от U₁ называемые характеристиками холостого хода трансформатора. Напряжение U₁ по значению практически равно ЭДС. . - описывает кривую намагничивания; следовательно так же имеет вид кривой намагничивания. Измеренная ваттметром мощность практически равна потерям мощности в магнитопроводе, пропорциональным квадрату магнитного потока или напряжения и зависимость имеет вид пораболы. Кроме того, из опыта холостого хода можно определить коэффициент трансформации трансформатора: k = Е₁/Е₂ = U₁₀/U₂₀.

Билет 33. Работа трансформатора под нагрузкой.

для первичной обмотки справедливо уравнение . - можно пренебречь и считать что

, откуда при U₁ = coпst и f = const получим, что .

Так как магнитным потоком во вторичной обмотке индуцируется ЭДС Е₂, то к ней можно присоединить электроприемник (нагрузку) Z_н (рис. 7.15). Под действи­ем этой ЭДС в замкнутой цепи вторичной обмотки возни­кает ток I₂. В первичной обмот­ке сама обмотка играет роль внешней цепи и ток I₁, в ней направлен от начала обмотки. В цепи вторичной обмот­ки внешней цепью является электроприемник, поэтому вторичный ток I₂ следует направить от начала обмотки к электроприемнику. Вторичный ток I₂ создает МДС I₂w₂, которая, в свою очередь, создает вторичный магнитный поток Ф₂, кото­рый замыкается в основном по магнитопроводу (см. рис. 7.15а). Теперь . Вследствие этого в первичной обмотке возникает допол­нительная составляющая тока I_1k, называемая компен­сационным током. Чем больше ток I₂, тем больше ток I_1к и, следовательно, больше ток первичной обмотки I_1k и мощность . Сначала электриче­ская энергия преобразуется в энергию магнитного поля, а затем энергия магнитного поля снова преобразуется в электрическую энергию.

Б илет 34. Короткое замыкание трансформатора.

Р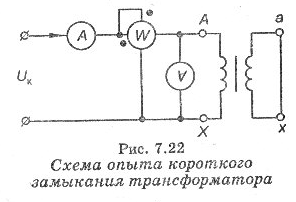 ежимом короткого замыкания трансформатора на­зывают такой режим, когда выводы вторичной обмотки замкнуты проводом с сопротивлением, равным нулю (Z_н = 0). Короткое замыкание трансформатора в услови­ях эксплуатации создает аварийный режим, так как вто­ричный ток, а следовательно, и первичный увеличива­ются в несколько раз по сравнению с номинальным. По­этому в цепях с трансформаторами предусматривают защиту, которая при коротком замыкании автоматиче­ски отключает трансформатор. Напряжение короткого замыкания. Напряжение U_K, при котором I₁= I_1ном называют напря­жением испытательного короткого замыкания трансфор­матора или просто напряжением короткого замыкания. Это напряжение обычно выражают в процентах от номинального напряжения U_1номи обозначают u_к, причем . Напряжение короткого замыкания зависит от выс­шего напряжения обмоток трансформатора и увеличива­ется с его повышением. Так как при коротком замыкании вторичной обмот­ки трансформатора напряжение на ее зажимах U₂ = 0, уравнение напряжения для нее принимает вид , уравнение записывается как . Этому уравнению соответ­ствует схема замещения транс­форматора, изображенная на рис. 7.20. Векторная диаграмма трансформатора при коротком замы­кании. Напря­жение короткого замыкания U_к имеет активную U_ка и ре­активную U_кр составляющие. Угол φ_к между векторами на­пряжения и тока зависит от соотношения между активной и реактивной индуктивной составляющими сопротивле­ния трансформатора . Поэтому считают, что у трансформаторов большой мощности U_к = U_кр, а полное сопротивление Z_к = Х_к. Опыт короткого замыкания проводят для определения параметров трансформатора. Собирают электрическую цепь, соответ­ствующую схеме (рис. 7.22), в которой вторичная обмот­ка замкнута накоротко металлической перемычкой или проводником с сопротивлением, близким к нулю. Р_пк- Ее называют электрическими потерями или потерями короткого замыкания. По данным измерений определяют следующие три параметра трансформатора: 1) напряжение короткого замыкания u_к=(U_к/U_1ном)*100%; 2) мощность потерь короткого замыкания Р_пк при I₁ =I_1ном; 3) потное, активное и индуктивное сопротивления трансформатора: ; ; . 3ная сопротивления Z_к R_к и Х_к; трансформатора, мож­но построить треугольник напряжений короткого замы­кания (треугольник 0АВ на рис. 7.21), а также опреде­лить активную и индуктивную составляющие напряже­ния короткого замыкания: ; .

Билет 36. Потери мощности и КПД трансформатора.

Подводимая к трансформатору энергия определяется мощностью Р₁ = U₁I₁cosφ₁ а энергия, отдаваемая транс­форматором электроприемнику, определяется мощностью Р₂ = U₂l₂cosφ₂. Разность Р_п = P₁ – Р₂ представляет собой мощность потерь в трансформаторе. Чем больше мощность трансформатора, тем меньше мощность потерь в нем. Коэффициент полезного действия трансформатора η = Р₂/Р₁. КПД трансформатора опре­деляют косвенным путем по формуле . Мощность потерь в трансформаторе складывается из мощности потерь Р_п0 в магнитопроводе и мощности по­терь Р_пэ, в обмотках: Р_п = Р_п0+ Р_пэ. Мощность потерь на нагрев обмоток Р_пэ = I'₂²R_к= I₁²R_к . Используя выражение для коэффициента нагруз­ки трансформатора , откуда , получим выражение для мощности потерь ,

г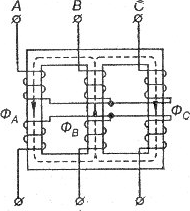 де Р_пк- потери в обмотках, определяемые в опыте ко­роткого замыкания при I_1ном, указываемые в паспорте трансформатора или в каталоге на трансформаторы, где этот вид потерь обозначен как Р_к, а значение приведено в киловаттах. Таким образом, ; следовательно . По этой формуле можно рассчитать КПД для любого значения нагрузки и cosφ₂. Продифференцировав выра­жение , получим, что η максимален при условии т. e. при равенстве мощности потерь холостого хода и короткого замыкания, откуда оптимальный коэффициент нагрузки .

Билет 37. Трехобмоточные и трехфазные трансформаторы.

Трехобмоточные трансформаторы являются самыми распространенными среди силовых миогообмоточных трансформаторов. Одна обмотка является первичной, к вей подводят напряжение U₁ от источника питания. Остальные обмотки - вторичные, к ним подключают нагрузку. На вторичных обмотках имеем различное на­пряжение. По уровню напряжения различают обмотки высшего напряжения (ВН), среднего (СН) и низшего (НН). Трех­обмоточные трансформаторы применяют тогда, когда необходимо передавать электроэнергию на различные расстояния (чем больше расстояние передачи, тем боль­шее напряжение требуется), а также для связи электрических сетей различного напряжения. Урав­нения ЭДС обмоток остаются неизменными, а уравне­ние токов имеет вид , где I₀ - ток холостого хода; I ₁ - ток первичной обмот­ки; I'₂ и I'₃ - приведенные токи вторичных обмоток. Трансформатор имеет три коэффициента трансфор­мации: ; ; ; и три напряжения короткого замыкания: u_к12; u_к13; u_к23;

Магнитная система трехфазных трансформаторов имеет два конструктивных исполнения. На рис. 7.26а изображен трехфазный трансформатор, состоящий из трех однофазных. Такой трансформатор называют трехфазным групповым. Каждая из трех фаз имеет самостоятельный

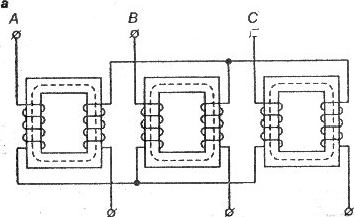
магнитопровод, поэтому электро­магнитные процессы в каждой из фаз протекают самостоятельно. Трехстержневой трансфор­матор имеет связан­ную магнитную систему. Первич­ная и вторичные обмотки каж­дой фазы располагают на одном стержне. В любой момент времени направление фазных магнитных потоков в стержнях таково, что их сумма равна нулю. Путь замыкания через крайний стержень длиннее, чем через средний, и поэтому общее магнитное сопротивление для потока край­ней фазы больше, чем для потока средней фазы. Поэтому для создания симметричной системы фазных потоков требуются разные МДС фаз I₀w₁: для средней фазы, имею­щей меньшее магнитное сопротивление, требуемая МДС меньшая, чем для крайних фаз. Следствием этого явля­ется несимметричная система токов холостого хода, при которой ток I_0B меньше, чем токи I_0A и I_0C. При больших мощностях трех­стержневые трансформаторы не применяют, поскольку в этом случае возникают трудности в технологии их изготовления. Кроме того, такие трансформаторы очень гро­моздки и их трудно транспортировать. Поэтому при боль­ших мощностях используют групповые трансформаторы, которые к тому же имеют некоторое преимущество пе­ред трехстержневыми по условиям резервирования (в ка­честве резерва у них достаточно иметь одну фазу).

Билет 39. Измерительные трансформаторы.

Д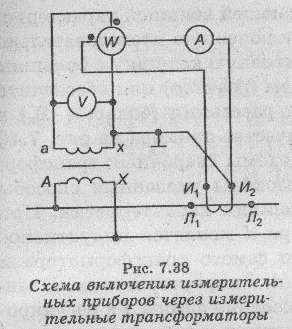 ля расширения пределов измерения приборов и для изоляции их от цепей высокого напряжения при­меняют измерительные трансформаторы: трансформато­ры тока и трансформато­ры напряжения. Трансформато­р тока используют для расширения пределов измерения амперметров и последовательных обмоток ваттметров, счетчиков энергии и фазометров. Его первичную обмотку включают последовательно в ту цепь, ток в которой надо измерить. K зажимам вторичной обмотки подключают амперметр или последовательные обмотки ваттметра, счетчика и фазометра. Чтобы ток во вторичной обмотке был, меньше измеряемого первич­ного тока, число витков вторичной обмотки делают большим. Вторичную обмотку и металлические части ко­жуха заземляют. Подключаемые ко вторичной об­мотке приборы обычно имеют небольшое сопротивление. Поэтому для трансформатора нормальным режимом является режим короткого замыкания при котором можно считать . При от­ключении или замене прибора вторичная обмотка транс­форматора тока должна быть обязательно закорочена. Для трансформаторов тока, как и для силовых трансформато­ров, справедливо уравнение МДС . Трансформаторы тока имеют стандартные номинальные первичные токи от 5 до 15000 А при номинальном вторичном токе 5 А.

Трансформаторы напряжения применяют в сетях высокого напряжения для измерения напряжения и часто­ты. K вторичной обмотке подключают вольтметры, часто­томеры и параллельные обмотки ваттметров, счетчиков и фазометров, т. е. обмотки, имеющие большое сопротивле­ние. Поэтому для трансформаторов напряжения нормаль­ным режимом является режим холостого хода. Трансформаторы напряжения конструктивно мало отличаются от обычных силовых трансформаторов. Они имеют небольшую мощность и включаются в сеть так же, как обычные трансформаторы. Вторич­ная обмотка заземлена. Коэффициент трансформации выбирают таким, чтобы вторичное напряжение было равно 100 B.

Билет 35. Внешняя характеристика трансформатора.

Внешней характеристикой трансформатора называ­ют зависимость вторичного напряжения от тока на­грузки при постоянных значениях первичного напряжения и коэффициента мощности нагрузки:

.

При холостом ходе трансформатора можно считать, что U’₂ = U'₂₀ = U₁, поэтому U’₂ = U'₂₀-∆U

т. е. напряжение на вторичной обмотке отличается от напряжения при холостом ходе на значение потери напря­жения в трансформаторе. u'₂=u₂=100-∆u. Для трансформаторов большой мощности

u₂=100-βu_кsinφ₂. B си­ловых трансформаторах при cosφ₂=1 будет sinφ₂=0, и напряжение U₂ остается неизменным при всех значениях нагрузки. При активно-иидуктивной нагрузке φ₂ по­ложителен, и чем он больше, тем больше потери напря­жения и тем значительнее снижение напряжения U₂ с ростом тока нагрузки. При активно-емкостной нагрузке

φ₂ отрицателен и потеря напряжения ∆u =-βu_кsinφ₂ так­же отрицательна. Уравнение (7.20) принимает вид u₂=100+βu_кsinφ₂. С ростом β напряжение U₂ увеличивается по сравнению с U₂₀.

Для трансформаторов малой мощности нельзя пре­небрегать активной составляющей напряжения коротко­го замыкания. . Наличие составляющей U_ка обусловливает снижение напряжения U₂ при активной нагрузке и уменьшение отклонения напряжения от номинального значения при наличии реактивной составляющей тока нагрузки.

Билет 40. Сварочные трансформаторы.

В конструктивном от­ношении имеется большое разнообразие сварочных трансформаторов. B значительной степени это опреде­ляется видом сварки (дуговая, Стыкован, шовная, то­чечная). При дуговой сварке вольтамперная характеристика электрической дуги имеет вид, показанный на рис. 7.39 (кривая 1). Вольтамперная (илы внешняя) характеристика трансформатора, т. е. источника питания дуги, дол­жна иметь точки пересечения с вольтамперной харак­теристикой дуги, чтобы ее горение было устойчивым. Следовательно, сварочный трансформатора должен иметь крутопадающую внешнюю характеристику (кривая 2). Зажигание дуги происходит в точке А1 при напряже­нии 60...70 В, а устойчивое горение дуги - в точке А2 при напряжении 12...30 B и при большом токе. Для получения крутопадающей внешней характерис­тики можно использовать включенную последовательно с вторичной обмоткой индуктивную катушку с большим индуктивным сопротивлением (реактор) или обеспечить большие магнитные потоки рассеяния (большое Х_к) в самом трансформаторе.

Билет 38. Схемы и группы соединения обмоток трехфазного трансформатора.

П 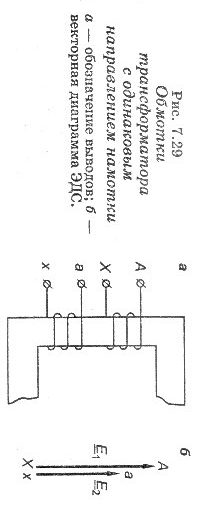ервичные и вторичные обмотки трехфазных транс­форматоров (групповых и трехстержневых) соединяют звездой или треугольником. B некоторых случаях об­мотки трансформаторов соединяют по схеме зигзаг. При соединении обмоток звездой с выводом нейтральной точки это соединение обозначают знаком ¥. Схемы со­единения первичной и вторичной обмоток двухобмоточ­ного трансформатора обозначают дробью, в числителе которой указывают схему соединения первичной обмот­ки, а в знаменателе - схему соединения первичной об­мотки, например Y/¥, ∆/∆, Ұ/∆. Схемы соединения об­моток трехобмоточтных трансформаторов обозначают сле­дующим образом: Y/У/∆. Обмотку высшего напряжения трансформатора с эко­номической точки зрения выгоднее соединять звездой, так как для получения заданного линейного напряже­ния U_л требуется фазное напряжение U_Ф = U_л /, и сле­довательно, меньшее число витков обмотки и меньший расход изоляционных материалов. Обмотка, соединен­ная треугольником, также имеет свои преимущества. При наличии обмотки, соединен­ной треугольнигсом, под дей­ствием ЭДС третьего поряд­ка в замкнутом треугольнике обмоток появится ток и падение напряжения в обмот­ках уравновесит ЭДС третьей гармоники. Линейные напря­жения обмотки, соединенной треугольником, будут сину­соидапьными. Поэтому у трансфорлаторов большой мощ­ности одну из обмоток обычно соединнют треугольникам. При использовании трехфазных трансформаторов в сложных системах с большим числом тронсформаций и при наличии параллельных ветвей с трансформаторами всегда необходимо знать сдвиг фаз между первичным и вторичным линейными напряжениями. Этот сдвиг ха­рактеризуется Группой соединения обмоток. Группу соединения обмоток трехфазного трансформатора обозначают цифрой часового циферблата, на которую указывает вектор линейной вторичной ЭДС при условии, что вектор линейной первичной ЭДС направлен на ноль часов. Для случая соединения первичной и вторичной обмо­ток звездой векторные диаграммы фазных и линейных ЭДС изображены на рис. 7.ЗОа. Сначала строят диаграмму фазных ЭДС (система ЭДС симметрична), диаграмму ли­нейных ЭДС строят на основании формул (4.3). Из век­торных диаграмм видно, что при совпадении по фазе фазных ЭДC линейные ЭДС первичной и вторичной об­моток также совпадают по фазе. Итак, группа соединения 0 получается при одинаковой схеме соединения первичной и вторичной обмоток. Эта группа соединения обозначает­ся Y/ Y - 0, ∆/∆ - 0. При соединении первичной обмотки звездой, а вторичной - Треугольником (СМ. рис. 7.286) получим Дру­гую группу соединения. Чтобы получить соединение вто­ричной обмотки треугольником, начало фазы а соединя­ют с концом фазы b и т. д. Векторная диаграмма ЭДС первичной обмотки (рис. 7.306) остается той же, что и на рис. 7.30а. Таким образом, при соединении первичной обмотки звез­дой, а вторичной - треугольником получили группу сое­динения 11 (Y /∆ - 11).

42. Дроссель в насыщенном магнитном состоянии

Дросселем называют электротехническое устройство пе­ременного тока, состоящее из обмотки и стального магни-топровода с регулируемым воздушным зазором δ (рис. 8.1). Наличие зазора позволяет изменять магнитное со­противление магнитной цепи, а следовательно, и ин­дуктивность L обмотки. При этом полное сопротивле­ние дросселя = также изменяется, что приводит к изменению тока в цепи и напряжения на элементе с сопротивлением Z . Магнитное сопротивление цепи и индуктивность обмот­ки можно изменять и при замкнутой магнитной цепи. С этой целью на магнито-проводе размещают дополни­тельную обмотку постоянно­го тока, предназначенную для подмагничивания стального сердечника. Это устройство называют дросселем насыще­ния (рис. 8.2).

Рассмотрим подробнее про­цессы, протекающие в дроссе­ле насыщения. Обмотку , на которую подают синусоидаль­ное напряжение (на рис. 8.2 комплексное напряжение U), называют рабочей обмоткой.

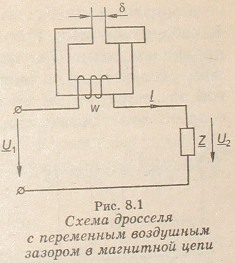
Последовательно с ней включают нагрузку (электроприемник) с сопротивлением Zн. Ток |_р в рабочей обмотке зависит от напряжения U , сопротивления нагрузки Zн и сопротивления Zp самой обмотки. Обмотку с числом витков Wy, которую подключают к источнику постоянного напряженияUy называют обмоткой управления. Токуправления Iy в ней можно изменять с помощью резистора с сопротивлением Ry.

При отсутствии тока в обмотке управления режим аналогичен режиму холостого хода трансформатора, когда магнитный поток в магнитопроводе определяется только магнитодвижущей силой первичной обмотки. Поэтому ток в рабочей обмотке является током холостого хода , значение которого мало. Если пренебречь активным сопротивлением рабочей обмотки Rp, то :

,

Где Rн – активное сопротивление нагрузки; - индуктивные сопротивления нагрузки и рабочей обмотки соответственно.

Сопротивление = определяется индуктивностью рабочей обмотки, прямо пропорциональной магнитной проницаемости . Так как магнитопровод работает в ре­жиме, соответствующем начальной (линейной) части кри­вой намагничивания, то его магнитная проницаемость и сопротивление Х_р велики. При этом .

Ток в рабочей обмотке и электрояриемнике (нагруз­ке), а также мощность элек­троприемника Р_н ⁼ очень малы. На рис. 8.3 по­казано изменение синусои­дального магнитного пото­ка Ф-1, создаваемого рабочей обмоткой в этом режиме, и тока холостого хода ( ), найденное с помощью кривой намагничивания. Ток изменяется по синусоидальному закону, так как дроссель работает в начальной линейной части кривой намагничивания.

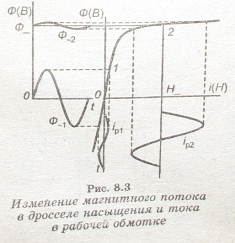
Обмотку управления выполняют из большого числа витков, чтобы при небольшом токе управления Iy со­здать достаточный магнитный поток. Если обмотку уп­равления подключить к источнику постоянного напря­жения U_у, то в ней появится ток I_У. При этом МДС I_vw_y обмотки управления создаст в магнитопроводе дросселя постоянный магнитный поток подмагничивакия Ф_. Маг­нитное состояние магнитопровода, обусловленное магни­тодвижущей силой обмотки управления, может опреде­ляться любой точкой на кривой намагничивания (рис. 8.3) от точки 0 до точки 2.

Если обмотка управления создает такую напряжен­ность магнитного поля Н_ , что магнитное состояние маг­нитопровода определяется точкой 2, расположенной на участке насыщения кривой намагничивания, то магнит­ная проницаемость µ = В/Н магнитопровода резко пада­ет (рис. 8.4а). С уменьшением магнитной проницаемо­сти уменьшаются индуктивность рабочей обмотки и ее индуктивное сопротивление. При неизменном сопротив­лении нагрузки Zн происходит перераспределение паде­ний напряжения: U= Up + Uн ,

где Up = jXp Ip — падение напряжения на рабочей обмот­ке дросселя насыщения; Uн= Zн *Iн - падение напряже­ния на нагрузке.

В режиме постоянного подмагничивания в связи с уменьшением магнитной проницаемости µ имеет место соотношение Х_р «Z_H. Поэтому падение напряжения Up на рабочей обмотке при U= const становится незначительным, а Uн . Для рабочей обмотки (при Rp=0) можно считать, что Up= Ep= 4,44*f* . Так как напряжение Up резко уменьшается, то уменьшается и переменный магнитный поток, создаваемый рабочей об­моткой (на рис. 8.3 он обозначен как Ф~₂ и сложен с потоком Ф- обмотки управления). Ток i_Р2 в рабочей об­мотке в этом режиме может быть найден графическим построением (см. рис. 8.3).

Из зависимости i_p2 = f(t) видно, что ток в рабочей обмотке и в нагрузке значительно увеличивается и ста­новится несинусоидальным, причем степень несинусоидальности зависит от характера кривой намагничивания. Если увеличивать I_У (рис. 8.4б) от нуля до номинального значения, то действующее значение эквивалентного си­нусоидального тока I_Р в рабочей обмотке увеличивается от значения тока холостого хода I_ро до максимального, значения, определяемого соотношением: Ip= U/Zн.

Таким образом, изменяя весьма малый (десятки мил­лиампер) ток Iy, в обмотке управления, оказывается воз­можным изменять большой по значению рабочий ток или напряжение на нагрузке.

43. Простейший магнитный усилитель.

Итак, дроссель насыщения выполняет функцию усилителя тока и мощ­ности нагрузки. При этом ток управления I_У играет роль входной величины, а рабочий ток I_Р — выходной. Одна­ко дроссель насыщения имеет существенный недостаток, заключающийся в том, что переменная составляющая магнитного потока рабочей обмотки, замыкающаяся по магнитопроводу, индуцирует в обмотке управления пе­ременную ЭДС, как и во вторичной обмотке трансформа­тора. Эта ЭДС создает переменный ток в цепи управле­ния, что приводит к искажению процессов, рассмотрен­ных ранее, и к искажению входного сигнала.

Для устранения этого недостатка простейший маг­нитный усилитель делают с двумя магнитопроводами (рис. 8.5). Обмотка управления _у охватывает внутрен­ние сердечники, поэтому магнитный поток подмагничи-вания Ф_ в обоих магнитопроводах всегда одинаков. Рабочую обмотку разделяют на две равные части, каждую из которых размещают на одном магнитопроводе. Эти части включены между со­бой последовательно таким образом, чтобы создаваемые ими переменные магнитные потоки Ф~ в каждый момент времени во внутренних сер­дечниках были направлены в противоположные сторо­ны. При этом суммарный переменный магнитный по­ток, сцепленный с обмоткой управления, равен нулю и, следовательно, в ней не бу­дет индуцироваться пере­менная ЭДС.

На рис. 8.6 приведена принципиальная схема про­стейшего магнитного уси­лителя. Здесь, как и в дрос­селе насыщения, ток в ра­бочей обмотке зависит от тока управления I_У аналогично тому, как показано на рис. 8.46. Эту зависимость называют нагрузочной ха­рактеристикой магнитного усилителя.

Коэффициентом усиления магнитного усилителя по мощности называют отношение приращения мощности Р_ВЫХ на выходе усилителя (в приемнике) к приращению мощности Рвх на его входе (в цепи управления):

(8.1) ,

>

где Р_н — мощность нагрузки при токе управления I_у > 0; Р_но — мощность нагрузки при I_у = 0; Р_у — мощность обмотки управления.

Магнитный усилитель имеет ряд достоинств по срав­нению с другими видами усилителей. К ним относятся высокая надежность работы, большой срок службы, от­сутствие движущихся частей.

Простейший магнитный усилитель, изображенный на рис. 8.5, имеет недостатки. Одним из основных недостатков такого усилителя является небольшой коэффициент (обычно При постоянных напряжениях обмотки управления Uy = Uвх и нагрузки Uн = Uвх коэффициент усиления (8.1) по мощности пропорционален коэффициенту усиления по току, который тем больше, чем больше угол наклона нагрузочной характеристики к оси абсцисс (см. рис. 8.4). К другим недостаткам относятся независимость рабочего тока от полярности тока управления (см. рис. 8.4) и наличие тока холостого хода Ipo ( тока в рабочей обмотке при отсутствии тока в обмотке управления).

Все недостатки простейшего магнитного усилителя можно устранить, применяя дополнительные обмотки и видоизменяя схему усилителя).