46. Модель дуополии по Курно.

Предположим, что две фирмы, A и B, производят аналогичный продукт. Обозначим через и 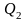объёмы выпуска продукции соответственно фирмами A и B. Пусть – совокупный объём выпуска продукции фирмами. Поскольку мы рассматриваем ситуацию дуополии, величина Q характеризует объём предложения на рынке.

Для описания зависимости цены единицы продукции от величины предложения на рынке воспользуемся функцией , , 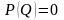если . Параметр a имеет смысл цены единицы продукции в случае, если .

Для описания зависимости затрат на создание единицы продукции от масштаба производства введём в модель функции затрат , фирм. Функция отражает факт равенства предельных затрат (параметр c) на производство единицы продукции для рассматриваемых фирм A и B.

Обозначим множества стратегий фирм символами и . объёма выпуска продукци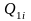и и ,

.

Для расчёта прибылей фирм воспользуемся формулой:

, .

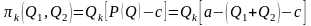Если пара существует, то для её поиска фирмы решают следующие задачи:

, .

Решим задачу максимизации прибыли для фирмы A.

.

Воспользуемся необходимым условием существования экстремума.

Получаем, что .

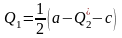Для фирмы B:

,

,

.

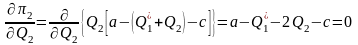Можно показать, что полученные выражения определяют объёмы выпуска, доставляющие максимумы прибыли Таким образом, можно записать следующую систему:

.

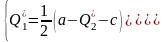
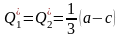Рис. Кривые реакций фирм.

46. Модель дуополии по Бертрану.

Рассмотрим теперь ситуацию, когда две фирмы A и B производят однородный продукт. Предположим, что A и B одновременно и независимо объявляют цены, соответственно и , по которым они готовы продавать свою продукцию. Тогда величина спроса на рынке для фирм A и B будет формироваться по следующему правилам соответственно:

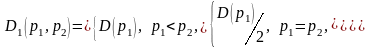и

Рассмотрим условия, при которых пара образует равновесие по Нэшу. Предположим равенство предельных затрат c фирм на выпуск продукции. Очевидно, что , , т.к. назначение цены ниже предельных затрат приведёт к отрицательной прибыли фирм.

С другой стороны, не может быть выше c. Рассмотрим это утверждение более подробно. Предположим для определённости, что , тогда если , то фирма B, сталкивающаяся в этом варианте в лучшем случае с половинным спросом, может «перехватить» весь спрос, назначив цену , . Если же , то фирма A, аналогично, может назначить цену , «перехватывая» весь спрос.

Таким образом, в равновесии по Бертрану (или в равновесии по Нэшу в дуополии по Бертрану) , и фирмы получают нулевую прибыль. Эту ситуацию называют парадоксом Бертрана.

Случай дифференцируемых продуктов. Фирмы A и B выбирают цены и одновременно и независимо. Предположим, что спрос, с которым сталкиваются фирмы, описывается для фирм A и B соответственно функциями:

, .

Стратегии фирм обозначим символами:

, .

Прибыли (выигрыши) фирм (игроков) могут быть определены в соответствии с функциями:

,

.

Если равновесная по Нэшу пара существует, то для её поиска фирмы решают следующие задачи:

, .

Решение задач запишем в виде:

.

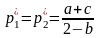Итак, оптимальные стратегии фирм A и B заключаются в выборе цен . В соответствии с определением равновесия Нэша, отклоняясь от данных уровней цен в единоличном порядке, фирмы могут лишь ухудшить своё положение, а именно, снизить свою прибыль.