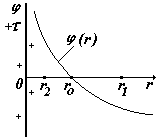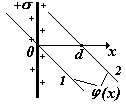- •2)Напряженность электростатического поля. Используя закон Кулона, получите выражение для напряженности поля точечного заряда.
- •4)Потенциал, разность потенциалов: выражения, физический смысл. Получите связь напряженности с разностью потенциалов для одномерного случая. Градиент потенциала.
- •6)Принцип суперпозиции (наложения) как фундам. Св-во полей. Дайте форм-ку, напишите общ. Выражение для напряж. И потенциала эл. Полей, созданных системой точечных зарядов и заряженными телами.
- •1)Поток вектора напряж. Теорема Гаусса, выраж, форм-ка. Примените теорему Гаусса для нахождения напряж. Поля метал. Сферы, заряженной с поверхностной плотностью заряда
- •2)Теорема Гаусса,выраж,форм-ка.Примените теорему Гаусса для нахождения напряж. Поля длинной прямой нити,равномер. Заряженной с лин плот.Заряда
- •3)Теорема Гаусса,выраж,форм-ка.Примените теорему Гаусса для нахождения напряж. Поля бесконечно длинного прямого полого цилиндра ,равномер. Заряженного с лин плот.Заряда
- •1) Точечный заряд.
- •2)Получите выражение для потенциала поля равномерно заряженной по поверхности сферы, считая известным выражение для напр. Поля. Укажите положение, где выбрано . Нарисуйте графики .
- •4)Получите выражение для потенциала поля равномерно заряженной бесконечно протяженной плоскости в зависимости от расстояния X от плоскости. Нарисуйте графики .
- •1)Распределение зарядов в проводниках.Найдите,используя теорему Гаусса,напряженность поля внутри и вблизи поверхности проводника,равномерно заряженного с поверх. Плот. Заряда
- •2)Покажите на примере 2 сфер радиусами r1 иR2,соединенных проводящей нитью,что заряды по сферам распред. С поверх. Плотностью (Влиянием нити пренебречь).
- •3)Явление эл.-ст. Индукции,возн. При внесении незар. Проводника в эл.-ст. Поле. Что такое индуцированные(наведенные)заряды? Что называют эл.-ст.Защитой?
- •1)Электроемкость уединенного проводника и конд. От чего зависит электроемкость? Получите выражение для электроемкости сферы радиуса r.
- •5)Выведите выражение для электроемкости при парал. И послед. Соединении конденсаторов.
- •1)Диполь и его электрический момент. Нарисуйте с помощью силовых линий и эквипотенц. Поверхностей поле диполя. Напряженность и потенциал поля диполя.
- •2)Поведение диполя во внешнем однородном и неоднородном эл. Полях.
- •3)Работа ,совершаемая при повороте диполя во внеш. Эл. Поле. Энергия диполя во внешнем поле.
- •4)Поляризация диэлектриков. Деформационная,ориентационная, и ионная поляризация.Поляризуемость молекул пол. И непол. Диэлектриков
- •5)Вектор поляризации.Вектор эл. Смещения.Диэл. Проницаемость и восприимчивость, их зависимость от температуры.Теорема Гаусса для диэлектриков.
- •1)Энергия точечного заряда во внеш. Эл. Поле. Энергия взаим-я системы точечных неподвижных зарядов.
- •3)Энергия эл.-ст. Поля. Получите выражение для объемной плотности энергии поля на примере плоского конденсатора.
- •1)Сила тока.Плотность тока.Получите выражение,связ. Плотность тока со средней скоростью носителей тока и их концентрацией.
- •2)Постоянный эл. Ток.Источники тока.Сторонние силы.Эдс источника.Разность потенциалов и напряжение.З-н Ома в инт. Форме дляоднородного и неод.Участков цепи ,для замкнутой цепи.
- •3)Электронная теория электропроводности металлов: основные предположения теории и вывод з-на Ома в диф. Форме. Затруднения теории электропроводности.
- •5)Эл. Сопротивление.Как объясняется сопротивление проводников на основе эл. Теории?Зав-ть сопротивления проводников от длины и площади сечения проводника.Уд. Сопр. Металлов,его зав-ть от темп.
- •1)Сила Лоренца как следствие опытных данных, ее эл. И маг. Составляющие. Напишите выражение для силы в векторном виде, укажите направления векторов. Дайте определение вектора магнитной индукции.
- •3)Напишите выр. Для маг. Индукции поля элемента тока(з-н Био-Савара-Лапласа) в век. И скал. Формах,сд. Рисунок,укажите напр. Векторов.Нап. Выр. И дайте форм-ку принципа суперпозиции для маг. Полей.
- •4)Получите с помощью з-на Био-Савара-Лапласа и принципа суперпозиции выр-ие для индукции маг. Поля прямого проводника с током (конечной длинны и бесконечно длинного).
- •1)Магнитное поле прямого проводника конечной длины.
- •2)Магнитное поле прямого бесконечно длинного проводника.
- •5)Получите с помощью з-на Био-Савара-Лапласа и принципа суперпозиции выр-ие для индукции маг. Поля на оси и в центре кругового тока. Маг. Момент контура с током.
- •3)Магнитное поле на оси кругового тока.
- •4) Магнитное поле в центре кругового тока
- •6)Нап. Выр. И дайте форм-ку теоремы о циркуляции вектора маг. Индукции. Получите с помощью этой теоремы выр-ие для индукции маг. Поля прямого бесконечно длинного проводника с током.
- •1) Прямой бесконечный проводник с током.
- •7)Напишите выр. И дайте форм-ку теоремы о циркуляции вектора маг. Индукции.Получите с помощью этой теоремы индукцию маг. Поля внутри длинного солиноида.
- •2) Индукция магнитного поля внутри длинного соленоида.
- •Тема 10
- •1)Сила, действующая на проводник с током в магнитном поле (сила Ампера), напишите выр. В век. И скал. Формах, сделайте рисунок, укажите направления векторов.
- •2)Получите выр. Для силы взаимодействия 2 прямых длинных параллельных проводников с токами.
- •3)Получите выр. Для вращающего момента, действ. На контур с током в магнитном поле.
- •1) Однородное поле.
- •4)Опишите поведение витка с током в однород. И неоднор. Маг. Полях. Напишите выр. Для силы,действ. На контур с током в неоднород. Маг. Поле.
- •5)Работа по перемещению проводника и контура с током в маг. Поле. Энергия контура с током во внешнем маг. Поле.
- •Тема 11
- •2)Получите выражение для эдс индукции, возн. В проводнике, движущемся в маг. Поле.
- •3)Явление самоиндукции. Эдс самоиндукции. Индуктивность (коэф. Самоиндукции) проводника.
- •4)Получите выр. Для индуктивности длинного соленоида.
- •Тема 12
- •1)Маг. Энергия проводника с током. Энергия маг. Поля. Получите выражение для объемной плотности энергии маг. Поля на примере длинного соленоида.
- •Тема 13
- •1)Хар-ки маг. Поля: индукция, напр-ть, намагн-ть, связь м/у ними. Маг. Проницаемость и восприимчивость вещества.
- •2)Теорема о циркуляции вектора индукции маг. Поля в магнетиках.
- •3)Пара- и диамагнетики, их маг. Св-ва. Качественное объяснение намагниченности этих вещ-в на основе представлений о магнитных моментах молекул. Диамагнетизм.
- •4)Ферромагнетики, их св-ва. Гистерезис. Применение ферромагнетиков.
- •1)Вихревое эл. Поле. Максвелловская трактовка явления эл.-маг. Индукции. Первое осн. Положение теории Максвелла: напишите мат. Выражение в инт. Форме и дайте форм-ку.
- •2)Ток смещеня. 2 основное положение теории Максвелла: нап. Мат. Выр. В инт. Форме и дайте форм-ку.
- •3)Сист. Ур-ий эл.-маг. Теории Максвелла. Поясните, что принцип. Нового внес м. В ранее известные з-ны эл-ва и магнетизма.
- •Тема 15
- •1)Свободные колебания .Диф. Ур-ие свободных гармонических колебаний и его решение. Амплитуда, период, круговая частота, фаза колебаний. Скорость и ускорение при колебаниях.
- •2)Пружинный маятник. Напишите диф. Ур-ие колебаний пруж. Маятника. Получите ф-лу для вычисления периода малых колебаний пруж. Маятника. Частота колебаний.
- •3)Мат. Маятник. Нап. Диф. Ур-ие колебаний и получите ф-лу для вычисления периода малых колебаний. Маятника. Частота колебаний.
- •4)Физ. Маятник. Нап. Диф. Ур-ие колебаний и получите ф-лу для вычисления периода малых колебаний. Маятника. Частота колебаний. Приведенная длина физ. Маятника.
- •5)Смещение, скорость и ускорение при гармонич. Колебаниях.
- •6)Энергия гарм. Колебаний. Средняя за период энергия гарм. Осциллятора.
- •Тема 16
- •1)Нап. Диф. Ур-ие затухающих колебаний и его решение, поясните все причины. Нап. Выр-ие для амплитуды при затух. Колебаниях, нар. График.
- •2)Выужденные колебания . Нап. Диф. Ур-ие затухающих колебаний и его решение. Нарисуйте график амплитуды колебаний в зависимости от частоты вынуждающей силы. Резонанс.
- •Тема 17
- •1)Волны. Продольные и поперечные, примеры. Волновой фронт и волн. Поверхность. Получите ур-ие плоской монохроматич. Бегущей волны. Длина волны, фаза и частота колебаий,фазовая скорость,волновое число.
- •2)Стоячие волны. Пол. Выр-ие для смещения, график. Укажите на графике узлы и пучности, дайте пояснения.
- •Тема 18
- •1)Эл.-маг. Волны. Поперечность электромагнитных волн. Скорость эл.-маг. Волны в среде и вакууме. Показатель преломления. Связь напряженностей эл. И маг. Полей в эл.-маг. Волне.
- •2)Плоская монохром. Бегущая волна как следствие ур-ий Максвелла: напишите выражения и сделайте рисунок.
- •3)Энергия эл.-маг. Волны. Вектор Пойнтинга и среднее значение его модуля. Интенсивность волны.
- •Тема 19
- •1)Интерференция света. Когерентность. Получение интерференционных картин. Оптическая разность хода. Условия максимумов и минимумов при интерференции. Применение интерференции.
- •2)Дифракция света. Качественное объяснение дифракции на основе принципа Гюйгенса-Френеля. Дифракционная решетка. Разрешающая способность оптических приборов.
- •3)Поляризация света. Естественный и поляризованный свет. Способы полученя поляризованного света.
1) Точечный заряд.
Подставим в формулу () выражение для напряженности поля точечного заряда. 1 и 2 – любые две точки на радиальной оси координат r. Примем 1 = 0 при
r1 , заменим 2 , r2 r получим (r).
|
|
|
2)Получите выражение для потенциала поля равномерно заряженной по поверхности сферы, считая известным выражение для напр. Поля. Укажите положение, где выбрано . Нарисуйте графики .
() |
Связь разности потенциалов с напряженностью для случая одной переменной х или r (математически это уравнение однотипно с () при замене х r) |
Из уравнений () или () можно найти разность потенциалов, если известна функция Е(r) или Е(r). Чтобы получить формулу для потенциала, следует выбрать уровень нулевого потенциала (так же, как в случае потенциальной энергии – см. механику). Обычно принимают = 0 на бесконечности, но для поля нити это невозможно (см. ниже).
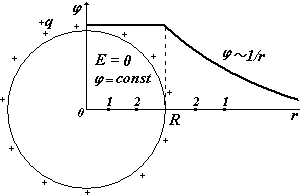
2).Сфера радиуса R, заряженная с поверхностной плотностью заряда (Кл/м2).
Полный заряд на сфере q = 4R2 . Будем рассматривать две области:1) выбираем две любые точки 1 и 2 в этой области и 2) также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу - потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
|
Подставим в () Е поля сферы. Для получается та же формула, что и для поля точечного заряда. |
|
|
|
|
|
3) Получите
выражение для потенциала
поля равномерно заряженной длинной
нити, считая известным выражение для
напр. поля и приняв потенциал
на расстоянии от нити
![]() Нарисуйте графики
.
Нарисуйте графики
.
() |
Связь разности потенциалов с напряженностью для случая одной переменной х или r (математически это уравнение однотипно с () при замене х r) |
3)Бесконечно длинная нить, заряженная с линейной плотностью заряда .
Выберем на оси радиальных координат r две любые точки с координатами r1 и r2.
(см. рис.). Подставим в () напряженность поля длинной нити и проинтегрируем.
|
В этом случае принять = 0 на бесконечности нельзя (см. график ln x), поэтому выбираем = 0 в некоторой произвольной точке с координатой ro. Т.е. примем заменим 2 , r2 r получим (r) |
|
= 0 при r = r0 |
|
|
4)Получите выражение для потенциала поля равномерно заряженной бесконечно протяженной плоскости в зависимости от расстояния X от плоскости. Нарисуйте графики .
() |
Связь разности потенциалов с напряженностью в интегральной форме для одномерного случая, когда Е(х) |
4)Бесконечно протяженная плоскость, равномерно заряженная с поверхностной плотностью заряда (Кл/м2). Выберем на оси координат х две произвольные точки х1 и х2 .). Используем формулу связи Е и (), подставим выражение для напряженности поля бесконечной плоскости.
|
Чтобы получить выражение для потенциала примем 1) 1 = 0 при х1 = 0 и 2) 1 = 0 при х1 = d (d – произвольная точка на оси х) |
1) 2) |
|
ТЕМА 4


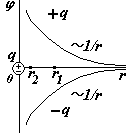

 1
= 0 при r1
= r0,
1
= 0 при r1
= r0,