3)Поляризация света. Естественный и поляризованный свет. Способы полученя поляризованного света.

Поляризация — для электромагнитных волн это явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H. Когерентное электромагнитное излучение может иметь:

• Линейную поляризацию — в направлении, перпендикулярном направлению распространения волны;

• Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции;

• Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями.

Некогерентное излучение может не быть поляризованным, либо быть полностью или частично поляризованным любым из указанных способов. В этом случае понятие поляризации понимается статистически.

При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. Тогда можно говорить о вертикальной и горизонтальной линейных поляризациях волны.

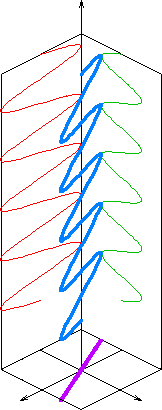
Линейная

Круговая

Эллиптическая

Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например поляризованные вертикально и горизонтально. Возможны другие разложения, например по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности.

Как с квантовой, так и с классической точки зрения, поляризация может быть описана двумерным комплексным вектором (вектором Джонса). Поляризация фотона является одной из реализаций q-бита.

Свет солнца, являющийся тепловым излучением, не имеет поляризации, однако рассеянный свет неба приобретает частичную линейную поляризацию. Поляризация света меняется также при отражении. На этих фактах основаны применения поляризующих фильтров в фотографии и т. д.

Линейную поляризацию имеет обычно излучение антенн.

По изменению поляризации света при отражении от поверхности можно судить о структуре поверхности, оптических постоянных, толщине образца.

Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света прошедшего через поляризаторы подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны.

Некоторые живые существа, например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например креветка-богомол павлиновая^[1] способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией.

1 Не обязательно брать цилиндр, можно взять любую призму, важно, чтобы ее образующие были перпендикулярны торцевым сечениям и самой заряженной плоскости.

2 Будем употреблять для краткости слово «емкость»

3Подумайте над вопросом: проводник заряжен зарядом 1 мкКл. Во сколько раз изменится его емкость, если заряд увеличить до 5 мкКл?

4 Силы F₂ и F₁ направлены по касательным к силовым линиям , а не горизонтально, как показано на рис., но мы будем этим небольшим различием пренебрегать.

5 Для газов использовать  неудобно, т.к. она очень мало отличается от единицы (для воздуха  = 1,000576), поэтому для газов чаще используют .

6 На границе двух диэлектриков силовые линии преломляются. При этом для вектора Е совпадают касательные составляющие, а отношение нормальных составляющих равно отношению диэлектрических проницаемостей. Для вектора D –наоборот (см. учебник).

7 Не приводим из-за громоздкости.

8 Если бросить заряженный металлический предмет – его движение можно считать кратковременным током. Если

вблизи находится компас, его стрелка даст отклонение, т.к. она реагирует на магнитное поле тока.

9 В металлах положительные заряды (ионы решетки) не могут перемещаться – они и есть сам металл.

10На вопрос, где работают сторонние силы ответить трудно. Натираем стеклянную палочку, дотрагиваемся до проводника, работают сторонние силы, а где? В батарейках сторонние силы работают только на границе проводника с электролитом. Внутри проводника всегда работают электростатические силы.

11 Открыт опытным путем нем. учителем Омом в 1827 г.В приведенных формулах интегралов нет, но формулы можно вывести из дифференциальной формы закона путем интегрирования (см. дальше по тексту).

12  - большая печатная греческая буква «омега».

13 Вычисления не приводим в силу их громоздкости, см. например, Матвеев А.Н. Электричество и магнетизм

14 В школьной физике силой Лоренца называют только магнитную часть полной силы (см. выражение ()).

15 Исторически сложилась путаница в терминологии. В электростатике силовая характеристика поля  напряженность Е, а вектор электрической индукции D  вспомогательный вектор, в магнетизме силовая характеристика поля - вектор магнитной индукции В, а вспомогательный вектор  вектор напряженности магнитного поля H.

16 О циркуляции – см. Электростатика

17 О циркуляции – см. Электростатика

18 В теории Максвелла два основных положения. В литературе существуют разногласия, какое из них называть первым, а какое вторм.

19 Для характеристики электрического поля можно использовать вектор напряженности Е или электрической индукции D, а для магнитного – вектор магнитной индукции В или вектор магнитной напряженности Н. Мы будем комбинировать эти векторы так, чтобы уравнения имели наиболее простой вид.

20 Если точка О совпадает с центром тяжести, тело будет находиться в положении безразличного равновесия

21 cos +cos =2cos(+)/2 cos()/2