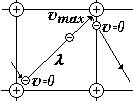
- •2)Напряженность электростатического поля. Используя закон Кулона, получите выражение для напряженности поля точечного заряда.
- •4)Потенциал, разность потенциалов: выражения, физический смысл. Получите связь напряженности с разностью потенциалов для одномерного случая. Градиент потенциала.
- •6)Принцип суперпозиции (наложения) как фундам. Св-во полей. Дайте форм-ку, напишите общ. Выражение для напряж. И потенциала эл. Полей, созданных системой точечных зарядов и заряженными телами.
- •1)Поток вектора напряж. Теорема Гаусса, выраж, форм-ка. Примените теорему Гаусса для нахождения напряж. Поля метал. Сферы, заряженной с поверхностной плотностью заряда
- •2)Теорема Гаусса,выраж,форм-ка.Примените теорему Гаусса для нахождения напряж. Поля длинной прямой нити,равномер. Заряженной с лин плот.Заряда
- •3)Теорема Гаусса,выраж,форм-ка.Примените теорему Гаусса для нахождения напряж. Поля бесконечно длинного прямого полого цилиндра ,равномер. Заряженного с лин плот.Заряда
- •1) Точечный заряд.
- •2)Получите выражение для потенциала поля равномерно заряженной по поверхности сферы, считая известным выражение для напр. Поля. Укажите положение, где выбрано . Нарисуйте графики .
- •4)Получите выражение для потенциала поля равномерно заряженной бесконечно протяженной плоскости в зависимости от расстояния X от плоскости. Нарисуйте графики .
- •1)Распределение зарядов в проводниках.Найдите,используя теорему Гаусса,напряженность поля внутри и вблизи поверхности проводника,равномерно заряженного с поверх. Плот. Заряда
- •2)Покажите на примере 2 сфер радиусами r1 иR2,соединенных проводящей нитью,что заряды по сферам распред. С поверх. Плотностью (Влиянием нити пренебречь).
- •3)Явление эл.-ст. Индукции,возн. При внесении незар. Проводника в эл.-ст. Поле. Что такое индуцированные(наведенные)заряды? Что называют эл.-ст.Защитой?
- •1)Электроемкость уединенного проводника и конд. От чего зависит электроемкость? Получите выражение для электроемкости сферы радиуса r.
- •5)Выведите выражение для электроемкости при парал. И послед. Соединении конденсаторов.
- •1)Диполь и его электрический момент. Нарисуйте с помощью силовых линий и эквипотенц. Поверхностей поле диполя. Напряженность и потенциал поля диполя.
- •2)Поведение диполя во внешнем однородном и неоднородном эл. Полях.
- •3)Работа ,совершаемая при повороте диполя во внеш. Эл. Поле. Энергия диполя во внешнем поле.
- •4)Поляризация диэлектриков. Деформационная,ориентационная, и ионная поляризация.Поляризуемость молекул пол. И непол. Диэлектриков
- •5)Вектор поляризации.Вектор эл. Смещения.Диэл. Проницаемость и восприимчивость, их зависимость от температуры.Теорема Гаусса для диэлектриков.
- •1)Энергия точечного заряда во внеш. Эл. Поле. Энергия взаим-я системы точечных неподвижных зарядов.
- •3)Энергия эл.-ст. Поля. Получите выражение для объемной плотности энергии поля на примере плоского конденсатора.
- •1)Сила тока.Плотность тока.Получите выражение,связ. Плотность тока со средней скоростью носителей тока и их концентрацией.
- •2)Постоянный эл. Ток.Источники тока.Сторонние силы.Эдс источника.Разность потенциалов и напряжение.З-н Ома в инт. Форме дляоднородного и неод.Участков цепи ,для замкнутой цепи.
- •3)Электронная теория электропроводности металлов: основные предположения теории и вывод з-на Ома в диф. Форме. Затруднения теории электропроводности.
- •5)Эл. Сопротивление.Как объясняется сопротивление проводников на основе эл. Теории?Зав-ть сопротивления проводников от длины и площади сечения проводника.Уд. Сопр. Металлов,его зав-ть от темп.
- •1)Сила Лоренца как следствие опытных данных, ее эл. И маг. Составляющие. Напишите выражение для силы в векторном виде, укажите направления векторов. Дайте определение вектора магнитной индукции.
- •3)Напишите выр. Для маг. Индукции поля элемента тока(з-н Био-Савара-Лапласа) в век. И скал. Формах,сд. Рисунок,укажите напр. Векторов.Нап. Выр. И дайте форм-ку принципа суперпозиции для маг. Полей.
- •4)Получите с помощью з-на Био-Савара-Лапласа и принципа суперпозиции выр-ие для индукции маг. Поля прямого проводника с током (конечной длинны и бесконечно длинного).
- •1)Магнитное поле прямого проводника конечной длины.
- •2)Магнитное поле прямого бесконечно длинного проводника.
- •5)Получите с помощью з-на Био-Савара-Лапласа и принципа суперпозиции выр-ие для индукции маг. Поля на оси и в центре кругового тока. Маг. Момент контура с током.
- •3)Магнитное поле на оси кругового тока.
- •4) Магнитное поле в центре кругового тока
- •6)Нап. Выр. И дайте форм-ку теоремы о циркуляции вектора маг. Индукции. Получите с помощью этой теоремы выр-ие для индукции маг. Поля прямого бесконечно длинного проводника с током.
- •1) Прямой бесконечный проводник с током.
- •7)Напишите выр. И дайте форм-ку теоремы о циркуляции вектора маг. Индукции.Получите с помощью этой теоремы индукцию маг. Поля внутри длинного солиноида.
- •2) Индукция магнитного поля внутри длинного соленоида.
- •Тема 10
- •1)Сила, действующая на проводник с током в магнитном поле (сила Ампера), напишите выр. В век. И скал. Формах, сделайте рисунок, укажите направления векторов.
- •2)Получите выр. Для силы взаимодействия 2 прямых длинных параллельных проводников с токами.
- •3)Получите выр. Для вращающего момента, действ. На контур с током в магнитном поле.
- •1) Однородное поле.
- •4)Опишите поведение витка с током в однород. И неоднор. Маг. Полях. Напишите выр. Для силы,действ. На контур с током в неоднород. Маг. Поле.
- •5)Работа по перемещению проводника и контура с током в маг. Поле. Энергия контура с током во внешнем маг. Поле.
- •Тема 11
- •2)Получите выражение для эдс индукции, возн. В проводнике, движущемся в маг. Поле.
- •3)Явление самоиндукции. Эдс самоиндукции. Индуктивность (коэф. Самоиндукции) проводника.
- •4)Получите выр. Для индуктивности длинного соленоида.
- •Тема 12
- •1)Маг. Энергия проводника с током. Энергия маг. Поля. Получите выражение для объемной плотности энергии маг. Поля на примере длинного соленоида.
- •Тема 13
- •1)Хар-ки маг. Поля: индукция, напр-ть, намагн-ть, связь м/у ними. Маг. Проницаемость и восприимчивость вещества.
- •2)Теорема о циркуляции вектора индукции маг. Поля в магнетиках.
- •3)Пара- и диамагнетики, их маг. Св-ва. Качественное объяснение намагниченности этих вещ-в на основе представлений о магнитных моментах молекул. Диамагнетизм.
- •4)Ферромагнетики, их св-ва. Гистерезис. Применение ферромагнетиков.
- •1)Вихревое эл. Поле. Максвелловская трактовка явления эл.-маг. Индукции. Первое осн. Положение теории Максвелла: напишите мат. Выражение в инт. Форме и дайте форм-ку.
- •2)Ток смещеня. 2 основное положение теории Максвелла: нап. Мат. Выр. В инт. Форме и дайте форм-ку.
- •3)Сист. Ур-ий эл.-маг. Теории Максвелла. Поясните, что принцип. Нового внес м. В ранее известные з-ны эл-ва и магнетизма.
- •Тема 15
- •1)Свободные колебания .Диф. Ур-ие свободных гармонических колебаний и его решение. Амплитуда, период, круговая частота, фаза колебаний. Скорость и ускорение при колебаниях.
- •2)Пружинный маятник. Напишите диф. Ур-ие колебаний пруж. Маятника. Получите ф-лу для вычисления периода малых колебаний пруж. Маятника. Частота колебаний.
- •3)Мат. Маятник. Нап. Диф. Ур-ие колебаний и получите ф-лу для вычисления периода малых колебаний. Маятника. Частота колебаний.
- •4)Физ. Маятник. Нап. Диф. Ур-ие колебаний и получите ф-лу для вычисления периода малых колебаний. Маятника. Частота колебаний. Приведенная длина физ. Маятника.
- •5)Смещение, скорость и ускорение при гармонич. Колебаниях.
- •6)Энергия гарм. Колебаний. Средняя за период энергия гарм. Осциллятора.
- •Тема 16
- •1)Нап. Диф. Ур-ие затухающих колебаний и его решение, поясните все причины. Нап. Выр-ие для амплитуды при затух. Колебаниях, нар. График.
- •2)Выужденные колебания . Нап. Диф. Ур-ие затухающих колебаний и его решение. Нарисуйте график амплитуды колебаний в зависимости от частоты вынуждающей силы. Резонанс.
- •Тема 17
- •1)Волны. Продольные и поперечные, примеры. Волновой фронт и волн. Поверхность. Получите ур-ие плоской монохроматич. Бегущей волны. Длина волны, фаза и частота колебаий,фазовая скорость,волновое число.
- •2)Стоячие волны. Пол. Выр-ие для смещения, график. Укажите на графике узлы и пучности, дайте пояснения.
- •Тема 18
- •1)Эл.-маг. Волны. Поперечность электромагнитных волн. Скорость эл.-маг. Волны в среде и вакууме. Показатель преломления. Связь напряженностей эл. И маг. Полей в эл.-маг. Волне.
- •2)Плоская монохром. Бегущая волна как следствие ур-ий Максвелла: напишите выражения и сделайте рисунок.
- •3)Энергия эл.-маг. Волны. Вектор Пойнтинга и среднее значение его модуля. Интенсивность волны.
- •Тема 19
- •1)Интерференция света. Когерентность. Получение интерференционных картин. Оптическая разность хода. Условия максимумов и минимумов при интерференции. Применение интерференции.
- •2)Дифракция света. Качественное объяснение дифракции на основе принципа Гюйгенса-Френеля. Дифракционная решетка. Разрешающая способность оптических приборов.
- •3)Поляризация света. Естественный и поляризованный свет. Способы полученя поляризованного света.
3)Электронная теория электропроводности металлов: основные предположения теории и вывод з-на Ома в диф. Форме. Затруднения теории электропроводности.
В электронной теории проводимости предполагается:
1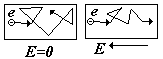 )
В металлах имеются свободные электроны,
которые в отсутствие внешнего
)
В металлах имеются свободные электроны,
которые в отсутствие внешнего
электрического поля движутся хаотически, а при
наличии поля приобретают характер упорядоченного
движения (см.рис.).
2) Движение каждого электрона подчиняется законам
классической механики.
3) Все вместе электроны образуют электронный газ и подчиняются законам
молекулярной физики.
4) Взаимодействие электронов с ионами решетки рассматривается как простое
столкновение, взаимодействием электронов между собой пренебрегается.
5) Напряженность поля внутри металла считается постоянной.
6) Все электроны под действием внешнего электрического поля приобретают
одинаковые скорости vср.
При выводе закона Ома будем считать, что электрон, сталкиваясь с ионом, полностью отдает ему свою энергию, а затем снова набирает скорость под действием сил поля (см. рис.- фрагмент кристаллической решетки). Электрон в кристалле участвует одновременно в двух движениях: хаотическом тепловом со скоростью u 105 м/с и направленном под действием поля со скоростью vср порядка 0,001 м/с, т.е. u vср
|
II закон Ньютона для электрона |
|
|
|
из кинематики, t – время движения электрона между двумя столкновениями |
||
|
средняя скорость электрона за время между двумя столкновениями |
||
|
- средняя длина свободного пробега электрона – это расстояние, которое проходит электрон между двумя последовательными столкновениями с ионами (u vср) |
||
|
плотность тока в проводнике; подставив в эту формулу вышеприведенные, получим: |
||
|
мы получили закон Ома в дифференциальной форме, запишем его в векторном виде: |
||
|
закон Ома в дифференциальной форме. В такой форме закон применим для бесконечно малого объема проводника, фактически – для точки проводника. |
|
|
|
- удельная электропроводность проводника; - удельное сопротивление проводника |
Электронная теория проводимости металлов, несмотря на множество упрощающих предположений, позволяет теоретически вывести закон Ома и закон Джоуля – Ленца (см. ниже). Это свидетельствует о том, что модель поведения электронов в металле соответствует действительности. Вместе с тем эта теория столкнулась с рядом трудностей. Рассмотрим некоторые из них.
1)Теплоемкость металла теоретически должно складываться из теплоемкости кристаллической решетки и теплоемкости электронов: СМе = Среш +Сэлнов=
6R/2 + 3R/2 (для моля). Но из опыта следует, что теплоемкость почти всех твердых тел равна 3R. Таким образом, получается, что электроны не участвуют в теплоемкости, т.е. не «принимают» тепло при нагревании вещества. В дальнейшем с развитием квантовой механики выяснилось, что электроны в металле могут иметь не любые энергии, а только те, значения которых лежат в разрешенных зонах (см. III часть курса).
2)В формуле () e,m известны, n, u – можно вычислить, а = 1/ измерить опытным путем. Таким образом можно оценить длину свободного пробега электрона . Она оказалась равной порядка 105 см, тогда как расстояние между ионами примерно 108 см. Получается, что электрон пролетает мимо сотен ионов, не сталкиваясь с ними. Это затруднение также объяснила квантовая механика: движение электрона в металле – это распространение некоторой волны, искажение этой волны происходит на примесях (чужеродных атомах), а их металле значительно меньше, чем атомов решетки.
3)Затруднение
возникло также с зависимостью сопротивления
от температуры. Из ()
следует, что удельное сопротивление
=1/
![]() ,
т.к. скорость теплового движения u
,
а остальные величины практически не
зависят от температуры. Но из опыта
следовало, что
Т. Квантовая
механика разрешила и это затруднение
,
т.к. скорость теплового движения u
,
а остальные величины практически не
зависят от температуры. Но из опыта
следовало, что
Т. Квантовая
механика разрешила и это затруднение
4)З-н Джоуля-Ленца: дайте формулировку и полчите з-н на основе электронной теория электропроводности металлов.
Закон Джоуля – Ленца: «Если по проводнику протекает ток, в проводнике
выделяется теплота Q». Найдем выражение для Q. Сначала получим закон в дифференциальной форме на основе электронной теории. Введем новое понятие:
|
удельная мощность – это энергия, выделяющаяся в единице объема проводника за единицу времени 12 |
|
энергия, передаваемая одним электроном иону решетки за одно столкновение, т.е. за время t время между двумя столкновениями. |
|
|
энергия, передаваемая электронами, находящимися в единице объема проводника за одно столкновение (за время t), n- концентрация электронов |
|
|
энергия, выделяющаяся в единице объема за единицу времени (формулы - см. закон Ома) |
|
|
закон Джоуля – Ленца в дифференциальной форме |
Чтобы найти
количество теплоты, выделяющейся во
всем проводнике за некоторое время
нужно проинтегрировать и использовать
закон Ома:
![]()
|
закон Джоуля - Ленца в интегральной форме |
при постоянной силе тока, R – общее сопротивление участка цепи |
|
для случая, когда сила тока зависит от времени |