
- •Предмет науки о надежности. Определение надежности (в узком и широком смысле).
- •Основные этапы и направления развития теории надежности.
- •Характерные особенности ис(асоиу) как сложной системы. Виды надежности ис(асоиу)
- •Надежность ис(асоиу) как комплексное свойство.
- •Понятие отказа, классификация отказов технических средств (тс)
- •Понятие безотказности; виды технического состояния объекта.
- •Понятие ремонтопригодности; восстанавливаемые и невосстанавливаемые объекты, ремонтируемые и неремонтируемые объекты. Показатели ремонтопригодности
- •Понятие долговечности; виды предельного состояния. Наработка, виды наработки; технический ресурс, остаточный ресурс; срок службы технического объекта. Показатели долговечности
- •Понятия сохраняемости и живучести объекта; достоверность информации, выдаваемой объектом. Показатели сохраняемости
- •Показатели безотказности (статистические и математические определения) для невосстанавливаемых объектов
- •Показатели безотказности (статистические и математические определения) для восстанавливаемых объектов
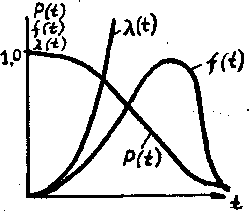
- •Связь между различными показателями надежности: вбр р(t), плотность f(t), средняя наработка до отказа t, интенсивность отказов λ(t)
- •Законы распределения дискретных случайных величин, применяемые в теории надежности: примеры дискретных случайных величин, распределение Пуассона и биномиальное распределение
- •Законы распределения непрерывных случайных величин, применяемые в теории надежности: закон Релея и закон Вейбулла
- •Законы распределения непрерывных случайных величин, применяемые в теории надежности: экспоненциальный закон и γ-распределение
- •Законы распределения непрерывных случайных величин, применяемые в теории надежности: нормальный и нормальный усеченный закон
- •Классификация и характеристика факторов, влияющих на надежность функционирования ис (асоиу)
- •Классификация методов расчета систем на надежность. Порядок расчета надежности. Расчет надежности при основном соединении элементов
- •Порядок расчета надежности
- •Резервирование. Классификация методов резервирования систем.
- •Кратность резервирования – это отношение числа резервных элементов объекта к числу основных.
- •Испытания на надежность: определение, значение Положительные и отрицательные стороны испытаний на надежность.
- •Классификация и краткая характеристика видов испытаний на надежность.
- •Определительные испытания на надежность (характеристика, виды, преимущества, недостатки).
- •Контрольные испытания на надежность, основанные на числе допустимых отказов, равном нулю (пример).
- •Контрольные испытания на надежность, основанные на последовательном анализе.
- •Понятие качества программных средств. Функциональные и конструктивные характеристики качества.
- •Иерархия показателей качества пс. Характеристика комплексных показателей качества пс
- •Классификация показателей качества. Процесс оценки показателей качества по гост
- •Показатели надежности пс; количественные характеристики критерия работоспособность.
- •Показатели надежности пс; количественные характеристики критерия устойчивость функционирования.
- •Понятия отказа и сбоя пс. Виды состояний (функционирования) по. Примеры
- •Классификация отказов по. Примеры
- •Понятие дефектов пс и причины их появления.
- •Области использования понятий отказ, сбой, дефект на протяжении всего жизненного цикла пс.
- •Объекты уязвимости, дестабилизирующие факторы и источники угроз надежности функционирования пс.
- •Модель анализа надежности пс.
- •Структурный анализ и структурные преобразования в расчетах надежности: преобразование структуры типа «треугольник» в структуру типа «звезда».
- •Структурный анализ и структурные преобразования в расчетах надежности: метод разложения сложной структуры по «ключевым элементам».
Законы распределения дискретных случайных величин, применяемые в теории надежности: примеры дискретных случайных величин, распределение Пуассона и биномиальное распределение
1. Биномиальное распределение – это
распределение при котором вероятность
возникновения или устранения ровно n
отказов объектов при N
независимых испытаниях определяется
формулой:
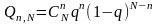 ;
;
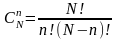
q – вероятность появления (устранения) одного отказав одном испытании
2. Распределение Пуассона – при q < 0,1. Qn,N=(1/n!)ane-a, где а=Nq
Законы распределения непрерывных случайных величин, применяемые в теории надежности: закон Релея и закон Вейбулла
1. Распределение Вейбулла
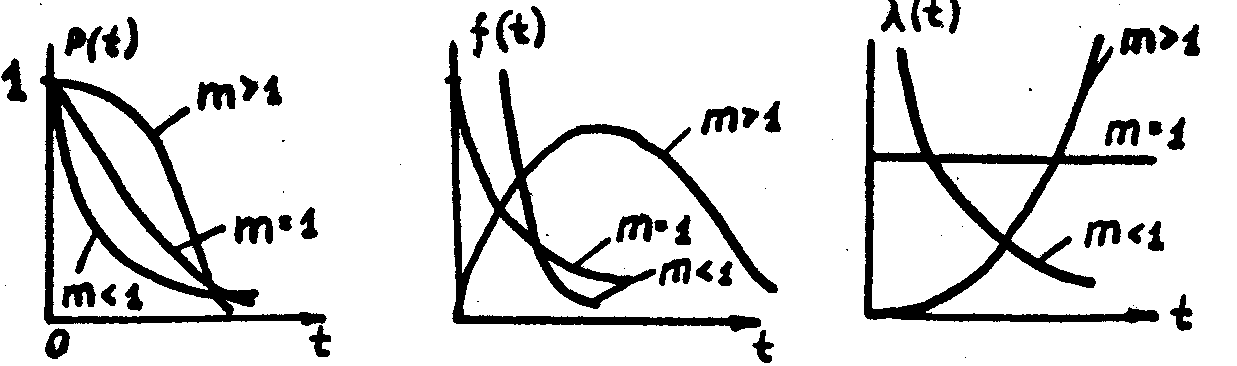
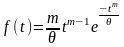 ,
t0,
m>0, >0.
m – параметр, определяющий
форму распределения;
,
t0,
m>0, >0.
m – параметр, определяющий
форму распределения;
- параметр, определяющий масштаб распределения.
Вероятность безотказной работы (ВБР)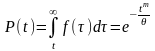
Средняя наработка до отказа
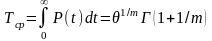
(t)=f(t)/P(t)=mtm-1/
при m=1, f(t)=(e-t/)/ - экспоненциальное распр.
при m=2, f(t)=(2/)exp(-t2/) – распределение Релея 2=/2
Характеризует при m>1 старение, износ; при m<1 - переработка
2. Распределение Релея.
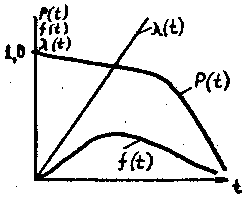
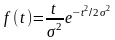 ;
;
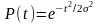 ;
;
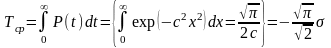 ;(t)=t/2
;(t)=t/2
Законы распределения непрерывных случайных величин, применяемые в теории надежности: экспоненциальный закон и γ-распределение
1. Экспоненциальное распределение
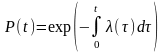 ;
(t)=f(t)/P(t).
При =const,
P(t)=e-t;
f(t)=e-t;
;
(t)=f(t)/P(t).
При =const,
P(t)=e-t;
f(t)=e-t;

- интенсивность отказов.
 При =const
– период нормальной эксплуатации.
При =const
– период нормальной эксплуатации.
Этот закон характеризует процессы возникновения и устранения отказов на этапе эксплуатации (=const)
2. Гамма-распределение.
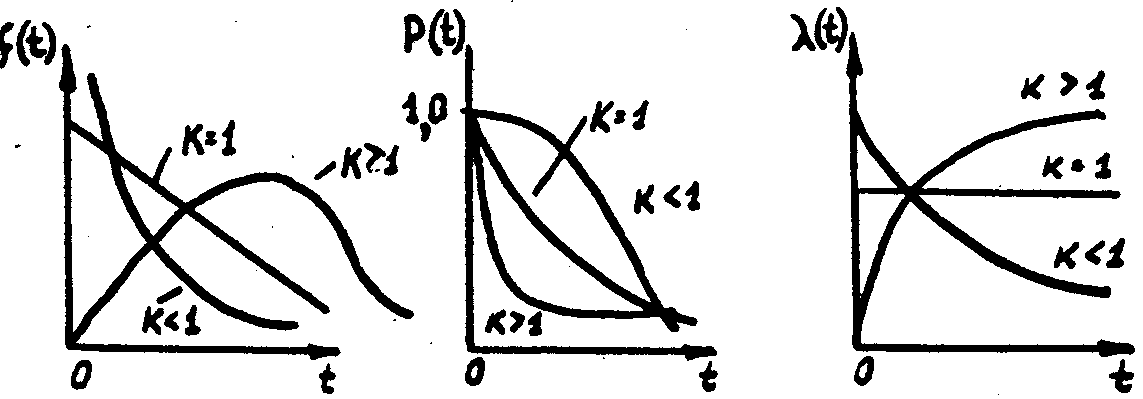
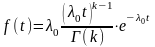 ;
;
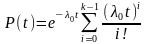 ;
;
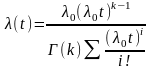 ;
Tcp=k/0
;
Tcp=k/0
k – определяет форму распределения; 0 – масштаб.
при k=1 – экспоненциальное распределение; if k – целое, то Г(k)=(k-1)!
Характеризует режим переработки
Законы распределения непрерывных случайных величин, применяемые в теории надежности: нормальный и нормальный усеченный закон
1. Нормальное и усеченное нормальное распределение.
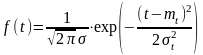
. Условие нормировки
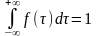
Tcp. Отсекаем часть кривой t<0 и вводим нормирующий множитель С.
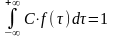
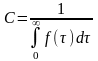
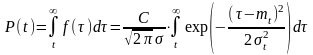
1.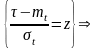
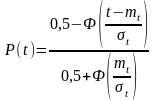 ,
где
,
где
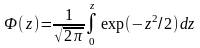
2.

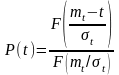 ,
где
,
где

F(-z)=1-F(z).
Усеченное нормальное распределение характеризует период старения, износа.
Нормальное распределение является предельным, к которому приближаются другие распределения при стремлении к бесконечности числа испытаний.
Классификация и характеристика факторов, влияющих на надежность функционирования ис (асоиу)
Факторы: аппаратные и неаппаратные.
Аппаратные: конструктивные (схемные) и производственные (технологические)
Неаппаратные: объективные и субъективные.
Объективные: качество ПО; условия и режимы работы (делится на внешние и внутренние).
Субъективные: квалификация обслуживающего персонала; обученность обслуживающего персонала; организация и качество технического обслуживания и регламентных работ; организация сбора и анализа сведений по надежности объекта; методы и способы организации и эксплуатации объекта.
25-40% отказов вызывается дефектом обслуживания (ошибки восприятия сигналов, запаздывание и ошибки в действиях операторов). if в системе > 2000 элементов, то при обслуживании систем с низкой квалификацией обслуживающего персонала средняя наработка на отказ = 0,74. При средней квалификации Tcр у> в 14 раз. При высокой – в 100 раз.
К конструктивным факторам относят:
1. правильный выбор структурной и функциональной схем, способов резервирования и контроля;
2. выбор материалов и комплектующих элементов;
3. выбор режимов и условий работы элементов в системе;
4. назначение требований к допускам на технические характеристики элементов;
5. качество разработки и эксплуатации документации.
Производственные факторы:
1. входной контроль качества мат-лов и элементов, получаемых от поставщиков;
2. организация технологического процесса изготовления оборудования;
3. контроль качества изделий на всех этапах технологического процесса;
4. квалификация изготовителей;
5. обеспечение качества и контроль монтажа и наладки оборудования;
6. условия и режимы работы на производстве.
