11. Принятие решения в условиях неопределенности: задача об оптимальном разложении фиксированной суммы денег на два вклада – рублевый и валютный.

При решении вопросов, связанных с инвестициями, заметную роль всегда играет фактор неопределённости : нет достаточно информации, как в будущем будут себя вести те или иные экономические показатели. В этой ситуации часто используются минимаксные решения: предпол-ие, что развитие событий пойдёт по наихудшему для инвестора сценарию и просч. алгоритм действий, кот. минимизирует потери инвестора в этой ситуации.

Пусть требуется различать некоторую фиксированную сумму S₀ денег на 2 вклада: рублевый и валютный, так чтобы в конце срока (пусть через год) наращенная сумма денег оказалась максимальной.

Пусть:

r – процентная ставка по рублевому вкладу

d – процентная ставка по валютному вкладу

K₀ – курс доллара к рублю в начальный момент

K₀ – курс доллара к рублю через год

Пусть для простоты S₀=1. Тогда, если x – вложения на рублевый вклад, то (1-х) – вложения на валютный вклад и ожидаемая рублевая масса через год будет равна:

Предположим сначала гипотетически, что К₁ известен. Найдем х, при котором S max

S’(x)=(1+r)- . Отсюда,

1.)Если 1+r> , т.е. если , то S_max будет достигаться при х=1 и что все деньги надо будет положить на рублевый вклад.

2.)Если 1+r< , т.е. если , то S_max будет достигаться при х=0 и что все деньги надо будет положить на валютный вклад.

Предположим, что будущий курс валюты неизвестен. Известно лишь, что

L

. Обозначим 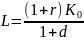. Случаи:

1.Случаи L<a и b<L нам неинтересны (ибо в этих случаях ясно как распоряжаться вкладом: положить х=0 при L<a, и х=1 при b<L)

K₁>L. Из этого следует S_max при х=0

2.K₁<L Smax при x=1

a

b

L

3. Пусть L .

Обозначим, I₁ .; I₂ . Пусть мы разделим вклад в пропорции х и (1-х). Тогда, если окажется, что К₁ I₁, то есть К₁<L, то величина недобора денег (по сравнению с максимально возможной) составит:

S(x)|_x=1 - S(x)=(1+r)-

Если же К₁ I₂, то величина недобора составит:

S(x)|_x=0-S(x)=

Вопрос: как же лучше всего распорядится выбором х?

Минимаксная стратегия – выбирают х так, чтобы минимизировать наибольший из этих недоборов.

При фиксированном х максимальное значение получают при К₁=а (К₁ ) и равно (*)

При фиксированном х максимальное значение ) получаются при К₁=b и равно (**)

Итак, нужно найти . Так как * - монотонно убывающая функция по х, а ** - монотонно возрастающая функция по х, то искомое х найдется из условия *=**.

Если решить уравнение, то . Это значение дает гарантированный результат: независимо от варианта реализации значения потери заведомо превысят минимальное значение, равного:

(надо ещё посчитать)

Это решение даёт гарантированный результат: независимо от варианта реализации, неопределённости , потери заведомо не превысят минимаксного значения, равного

12. Определение цен основных активов: задача об оптимальном портфеле ценных бумаг.

X – случайная величина (доход фирмы); S – некоторое состояние мира; – вероятность того, что мир будет находиться в состоянии S.

Ожидаемое значение случайной величины X (мат. ожидание):

Дисперсия (вариация):

Если заданы две случайные величины X и Y, то ковариация:

Можно показать, что ,

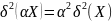
Оптимальный портфель ценных бумаг

N ценных бумаг, – доля i-ой бумаги в портфеле

r_i - доходность i-ой бумаги в интересующий момент времени

E(r_i ) – ожидаемая доходность; – дисперсия случ. величины r_i ; – ковариация случ. величин r_i и r_j

Доходность всего портфеля:

Ожидаемая доходность портфеля: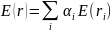

Дисперсия портфеля: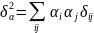

Пример:

При E(r) – const (заданной ожидаемой доходности) минимизировать дисперсию портфеля ;

Решение: (методом множителей Лагранджа)

Портфель минимизирующий риск находится из условия: