9.Дюрация облигации как денежного потока. Различные интерпретации понятия дюрации. Формулировка теоремы об иммунитете п. Самуэльсона.

Дюрация – чувствительность стоимости облигации к изменению процентных ставок.

Пусть r – процентная ставка,

С- выплата по купону,

F – номинальная стоимость облигации,

T – срок погашения (в годах).

Тогда P – текущая стоимость (цена) облигации.

.

Из этого следует:

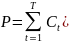
где C_t=C при t<T и С_t=C+F

Тогда,

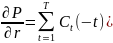
Отсюда

Левая часть характеризует процентное изменение цены облигации по сравнению с процентным изменением величины (1+r) – эластичность.

Введем 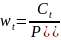– доля цены, которую вносит платеж в момент времени t. Тогда .

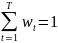Тогда , т.е. эластичность равна средневзвешенному времени с весами w_t

Дюрация такой облигации:

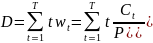
Чем меньше дюрация потока платежей, тем менее чувствительна современная величина потока к изменению процентной ставки.

Теорема об иммунитете (Пола Самуэльсона)

Финансовый портфель можно иммуницировать к изменению процентной ставки, выравнивая для этого текущие стоимости и дюрации, составляющие его активов и задолженностей.

10. Финансовые операции в условиях неопределенности: расчет суммарного капитала на счете в банке, на котором аккумулируются депозитные счета вкладчиков.

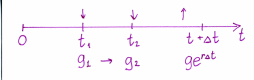
r-банковская ставка

x(t) – сумма всех депозитов в момент t

Предположим:

моменты поступления вкладов в банк описываются пуассоновским процессом, с плотностью , т.е.

P 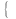за интервал длительностью T поступит ровно k вкладов =

, K=0,1,2…

Физический смысл - среднее число (математическое ожидание) вкладов, поступивших в единицу времени

Число вкладов, попавших непересекающиеся интервалы времени, являются независимыми случайными величинами.

Считаем что ф-ия F(x) – ф-ия распределения продолжительности вклада – подчиняется показательному закону, т.е

F(x) = P(вклад поступивший в момент T будет снят до момента

t)= 1 - , где 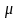- параметр, смысл которого в том, что 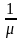= среднее значение продолжительности вклада

все вносимые вклады имеют один и тот же размер

взять обратно можно только весь вклад

x(t) – сумма всех вкладов в момент t; x(0)=0

Найдем средний размер капитала внесенного в промежуток

- среднее число вкладов в ед. времени

Х- число вкладов за промежуток времени Т

М - среднее число вкладов за время Т

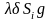- средний размер капитала, внесенного за промежуток

Найдем, в какую сумму превратится капитал K в момент t: 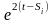< искомая сумма <

По непрерывности

искомая сумма =

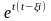
Тогда ( если считать, что вклады не забираешь обратно):

Х(t) = => М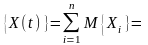

Учтем теперь то обстоятельство, что часть внесенных вкладов может не долежать до момента t ( их заберут)

Для этого заметим, что 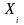- случайная величина со след.

знаком распределения:

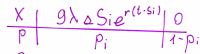
Где 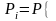продолж. вклада, внесенного в момент составит не менее ед. времени = 1 – P продолжительность вклада меньше = 1- F =

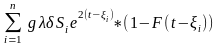
Наше рассмотрение будет тем точнее, чем больше n и меньше , поэтому точный результат М

Заменим переменную интегрирования u=t-s;ds=-du

= =T,u=0 =

Возможное соотношение параметров:

Если r> , 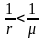, то М будет возрастать. Для банка это хорошо, но этот сценарий бывает крайне редко.

Будем интересоваться установившейся ситуаций продолжительного времени t→∞

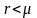если или , то М

Итак, при ( это имеет место в реальности):

Вопрос: сколько времени должно пройти чтобы М стало мало отличном от предельного значения

Ответ: Величина М = и отличается менее, чем на 1 %

Если t>