4. Расчет современной величины потока платежей в случае, когда моменты платежей являются случайными.

Пусть платежи С следуют друг за другом через случайные промежутки времени, распределены по показательному закону с параметром 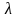>0

Нужно найти современную величину случайного потока платежей

С

t

0 1

t

С/(1+i)^T операция дисконтирования первого платежа в этом случае современную величину такого случ потока платежей естественно характеризовать мат ожиданием:

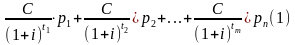
Но время Т -случайная величина, распределённая по показательному закону, т.е. с

плотностью распределения: f(t)= *е ^{- t}

где >0 – заданный параметр

Тогда мат ожидание совр величины первого платежа:

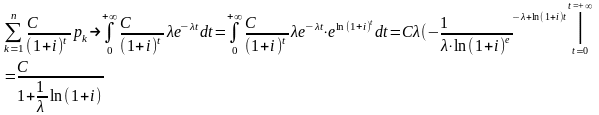Найдём мат ожид 2-го дисконтир платежа:

X – СВ – момент первого платежа

Z – СВ – момент 2го платежа,

При этом X – распр по показ закону, (z-x) – тоже по показ закону

СВ z будет иметь плотность распределения

Тогда современная величина потока из 2-х платежей будет равна

При n платежах:

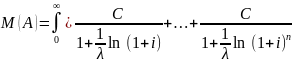
При n∞

M(A)= С/ ((1/λ)ln(1+i))

Если обозначить 1/λ = t_ср , то M{A}=С/(t_ср*ln(1+i))

5. Кредитные расчеты. Различные схемы погашения займов.

Кредит (заем, ссуда) –это предоставление денег (или товаров) в долг на условии возврата, причем как правило, с процентами.

Кредитор-тот, кто выдает деньги; Дебитор –тот, кто получает (заемщик). Сам заем- основный долг, а наращиваемый добавок –процентные деньги.

1. Погашение займа одним платежом в конце срока. Пусть займ D выдан на n лет под i сложных годовых процентов. К концу n-го года наращенная его величина станет: D(1+i)ⁿ.

2 Погашение основного долга одним платежном в конце срока:

Сам заем называется основным долгом, а наращиваемый добавок – процентными

деньгами. Пусть заем D выдан на n лет под i сложных годовых процентов. За 1-й

год процентные деньги составят i*D. В конце n-го, последнего, года

выплаты составят величину D+i*D. Общая сумма выплат= D+n*i*D

3. Погашение основного долга равными годовыми выплатами

В конце 1-ого года выплачивается: D/n + i*D

В конце 2-ого: D/n + i (D- D/n) = D/n + iD (1- 1/n)

В конце 3-ого: D/n + i (D- 2D/n) = D/n + iD (1- 2/n)

…..

В конце k-ого года: D/n + i (D – (k-1)D/n)

….

В конце n-ого года: D/n + i (D- (n-1)D/n) =>

= > Общая сумма выплат:

D + iD + i(D – D/n) + i(D – 2/n * D)+..+ i(D – (n-1)/n * D) = D + n*iD – iD/n (1+2+..+(n-1)) = D + n*iD – iD/n *(1+(n-1)/2) * (n-1) = D + n*iD – (n-1)/2 * iD = D + iD (n- (n-1)/2) = D + (n+1)/2 * iD

4. Погашение займа равными годовыми выплатами- такие выплаты можно рассматривать как годовую ренту длительностью n-лет и годовым платежом R. Современная величина ренты:

A= R/ (1+i) + R/ (1+i)² +…+ R/ (1+i)ⁿ= R* [1- (1+i) ^–n / i ] = R*a(n,i)

A=D

R= D/ a(n,i)

5. Погашение займа равными выплатами m-раз в год (в течение n-лет, под i %): Пусть y – величина такой выплаты, тогда величина разовой выплаты:

Y=

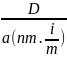
где

a(nm, i/m)=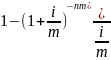

ПРИМЕР а : Пусть D = 5000$; n = 5 лет; i = 10%. Погашение равными годовыми выплатами =>

R = D/a(n,i) = 5000/a(5,10) = 5000/3,791 = 1319$

ПРИМЕР б : Пусть тот же займ погашается равными полугодовыми выплатами => Y(полугодовая) = D/a(2n, i/2) = 5000/a(10,5) = 5000/7,722 = 647$

Сравним: 1319$ * 5 = 6595$ / 647$ * 10 = 6470$