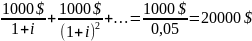Оглавление

1. Наращение и дисконтирование денежных сумм. Формулы простых и сложных процентов 2

2. Непрерывное наращение и дисконтирование денежных сумм. Связь со 2-м замечательным пределом 4

3. Потоки платежей. Конечная годовая рента. Вечная рента. 5

4. Расчет современной величины потока платежей в случае, когда моменты платежей являются случайными. 7

5. Кредитные расчеты. Различные схемы погашения займов. 8

6. Оценка инвестиционных проектов. Их основные характеристики: приведенный чистый доход, внутренняя норма доходности, срок окупаемости. 10

7. Доходность фин операций. Понятие мгновенной доходности. 12

8. Облигации. Курс и доходность: а) облигации без погашения с периодической выплатой купонных процентов; б) облигации с периодической выплатой процентов и погашением. 13

9.Дюрация облигации как денежного потока. Различные интерпретации понятия дюрации. Формулировка теоремы об иммунитете П. Самуэльсона. 14

10. Финансовые операции в условиях неопределенности: расчет суммарного капитала на счете в банке, на котором аккумулируются депозитные счета вкладчиков. 15

11. Принятие решения в условиях неопределенности: задача об оптимальном разложении фиксированной суммы денег на два вклада – рублевый и валютный. 19

12. Определение цен основных активов: задача об оптимальном портфеле ценных бумаг. 21

1. Наращение и дисконтирование денежных сумм. Формулы простых и сложных процентов

Основной принцип Фин вычислений: Принцип неравноценности денег в разные календарные сроки: Одинаковые суммы денег в данный момент (так сказать «сегодня») и в будущем – «завтра» оцениваются совершенно по-разному.

Принцип обусловлен следующим:

• возможностью рационального, продуктивного использования денежных средств как финансового актива, средства, приносящего доход

• возможным риском, который вызван неопределенностью в будущем.

НАЧИСЛЕНИЕ ПРОЦЕНТОВ:

пусть P – начальный вклад ( соответственно t в этот момент=0), а за i-обозначается процентная ставка( это значит, что на эту процентную ставку будет увеличиваться начальный вклад за какой-то определенный период T)

Пусть S-сумма в момент t=T, тогда:

S= P (1+i) (i>0 =>S>P)=> i=(S-P)/P

Если t=nT, то S(t) = P(1+i)ⁿ - сложная схема начисления процента

Тогда S(t)=P(1+in) – простая схема начисления процента, при этом n =1,2,3….

Сравним формулы простых и сложных процентов:

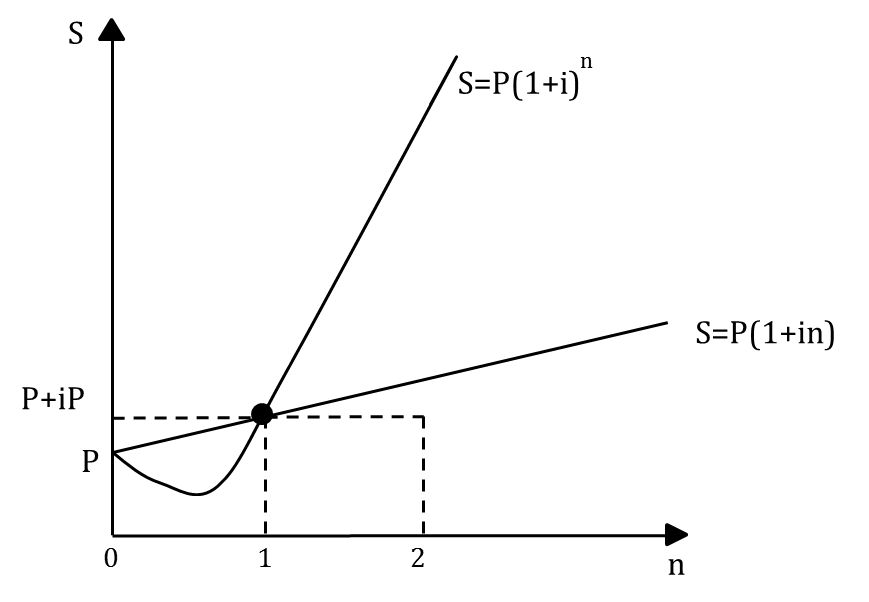
"Дисконтирующие и мультиплицирующие множители".

Некто претендует на сумму S через время t (см. рисунок 2).

Если он хочет получить эту сумму сейчас, то ему можно предложить сумму:

1)P = S/(1+it) - при схеме простых процентов.

2)P = S/((1+i)^t) - при схеме сложных процентов.

Множители 1/(1+it) и 1/((1+i)^t) называются дисконтирующими.

Обозначение:

D(n,i) = 1/((1+i)^n), - дисконтирующий множитель, где n - время в годах

Примеры: см. рисунок 3.

Обозначение:

M(i,n) = 1/(D(i,n)) = (1+i)^n - мультиплицирующий множитель.

"Эффективная ставка процента".

Пусть S(0) - имеющийся капитал в момент t = 0,

S(T) - имеющийся капитал в момент t = T.

По опред. эффективной ставкой процента называется ставка сложных процентов r_эф такая, что:

S(T) = S(0)*(1+r_эф)^T, т.е. r_эф = ( S(T)/S(0) )^(1/T) - 1.

2. Непрерывное наращение и дисконтирование денежных сумм. Связь со 2-м замечательным пределом

Непрерывным наращением по ставке i называется увеличение суммы в раз за единичный промежуток начисления и в общем виде увеличение суммы в 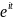раз за t промежутков начисления.

P – начальный вклад, i – годовая ставка процента, n раз в год – период начисления.

S=P(1+i) – сумма через год, если % начисляются 1 раз в год.

если 2 раза в год

Величина вклада через год S=P(1+i/n)ⁿ, n=1, 4, 12, …365…

При непрерывном наращении процентов вклад через год составит:

(теоритически можно считать, что n→∞)

В соответствии со вторым замечательным пределом:

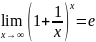
S(t)=P*e^it - формула непрерывного наращения процентов, если же рассматривается период не 1 год, а через t лет:

Непрерывным дисконтированием называется операция, обратная непрерывному наращению, т.е. уменьшение суммы в eⁱ раз за единичный промежуток и уменьшение в е^it раз за t промежутков.

S(0)=S(t)/e^it

3. Потоки платежей. Конечная годовая рента. Вечная рента.

a) Потоки платежей

Это множество распределенных во времени поступлений и выплат; при этом поступления берутся со знаком «+», а выплаты – с « - »

– поток платежей

C_k – платеж в момент времени;

t_{k –} момент времени

Пусть i – годовая ставка % (не изменяется)

С1 С2 С_{т C1 «+»; С2 « - »}

t=0 t1 t2 T

Сумма платежей, приведенная к моменту T, равна…

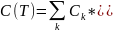
…и называется величиной потока платежей в момент Т (это к конечному моменту);

К начальному моменту:

Эта величина называется современная величина потока.

Если есть последний платеж С_Т, то величина потока в этот момент называется конечной величиной потока.

Поток положительных платежей с пост. промеж. между ними называется рентой.

Рента:

С1 С2 С_i C_i+1

0 t1 t2 t_i t_i+1

t_i+1 – t_i = const

b) Конечная годовая рента

Это поток одной и той же суммы С, поступающий раз в год в течении n лет (при постоянной ставке процента i)

Найдем современную величину такой ренты:

С С С C С

T (год)

0 1 2 j j+1 n

А – современная величина потока

А =

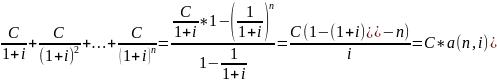
Величина а(n, i)^def = – коэффициент приведения ренты

Итак, современная величина ренты А = С*а (n,i)

Найдем конечную (наращенную) величину ренты:

Где коэфф. s(n,i) = – коэфф. наращения ренты

Зная любые 3 параметра из 5 , можно найти значения 2 оставшихся

c) Вечная годовая рента

Это рента последовательных платежей, которые являются неограниченными (математическое соответствие придуманному случаю )

Современная величина такой ренты равна…

Пример:

Городской житель арендует дачу за 1000$ в год. Какую сумму он должен предложить хозяину, если последний решит ее продать?

i=5%

1000$ 1000$

T

0 1 2

Оценка справедливой цены: