Билет №16.
1.Понятие равномощности двух множеств. Равномощность множеств точек двух произвольных отрезков.
Равномощны множества точек любых двух отрезков [a,b] и [с, d]. Множество точек любого отрезка равномощного множеству точек любого отрезка равномощного множеству точек любого его «подотрезка». Очевидно, что собственное подмножество конечного множества не может быть ему равномощно. Любое бесконечное множество равномощно разности этого множества и любого своего конечного подмножества.
Существует ли множество Х, при любом А удовлетворяющее равенству: а)(А Х) А = А ? б) (А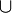
Х)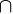
А = А ?
Билет №17.
1. Может ли какре-либо множество А быть равномощно своему подмножеству, отличному от множества А?
Нет, не может. Конечное множество А не может быть равномощно никакому своему подмножеству, отличному от А.