
Билеты по математике. Билет №1.
Понятие множества. Способы задания множеств. Свойства включения множеств. Универсальное множество. Пустое множество. Равенство и неравенство множеств.
Множество – это понятие не определяемое. Термин, который обобщает набор и совокупность. Множества состоят из элементов, обозначаются главными латинскими буквами (А, В), а маленькие эл-ты обозначатся (а, в). Множество может обозначать один элемент или несколько: А={a}; B={a, b}. Создан в конце 19 века Георгом Кантером, в Греции.
Способы задания множеств:
Перечисление. А = {a,b,c,d}
С помощью характеристического св-ва. М={x|x – точка на одной из сторон треугольника АВС.}
Свойства включения множеств:
А.) Любое множество является подмножеством самого себя, т.е. для любого множества А справедливо включение А Ϲ А. В этом случае А называют несобственным подмножеством А. Справедливость этого свойства вытекает непосредственно из определения подмножества.
Б.) Если А – подмножество множества В, а В – подмножество множества С, то А – подмножество множества С.
В.) Универсальное множество – это самое «большое» множество, содержащее в себе все множества.
Г.) Пустое множество – множество в котором нет ни одного элемента.
Равное множество – множества, состоящие из одних и тех же элементов.
Неравенство множеств – если хотя бы в одном множестве существует хотя бы один элемент, не принадлежащий другому множеству.
Доказать равномощность множества четных натуральных чисел и множество натуральных делящихся на 3.
Билет №2.
Пересечение множеств и свойства операции пересечения. Диаграммы Эйлера-Венна.
Пересечение множеств – это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам. Так, операцию пересечения двух множеств отождествляют с произведением чисел, а объединение этих множеств – с суммой чисел.
А![]() В
= В
А .
на диаграммах Венна изображаются все
возможные варианты пересечения множеств.
Количество пересечений (областей) n
определяется по формуле: n=2
в степени N.
Где N-кол-во
множеств.
В
= В
А .
на диаграммах Венна изображаются все
возможные варианты пересечения множеств.
Количество пересечений (областей) n
определяется по формуле: n=2
в степени N.
Где N-кол-во
множеств.
Какое из множеств является подмножеством другого: A, (A
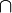 B)
, B
B)
, B
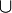 A
?
A
?
Билет №3.
Объединение множеств. Свойства операции объединения.
Объединение множеств – множество, состоящее из всех элементов, принадлежащих хотя ы одному из множеств.
Свойства операции объединения.Справедливы следующие равенства: 1. A∪B = B∪A 2. (А∪B) ∪C = А (B∪C). Объединение А и пустого множества равно А.
Какое из двух множеств является подмножеством другого: А, (А B) A ?
Билет №4.
Свойства, связывающие операции объединения и пересечения. Законы поглощения.
А v B = B v A (коммуникативность)
( A v B) v C = A (B v C) (ассоциативность)
Если А больше или равно В, то А v B = A
Объединение А и пустого множества равно А.
Доказать равномощность множеств точек двух окружностей радиусов 5 см и 10см соответственно.
