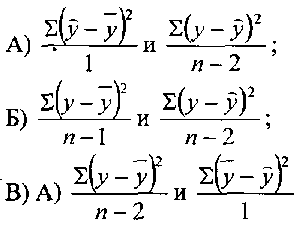Вариант XVI
1. Коэффициенты множественной корреляции позволяют:
а) выявить связь между одной и многими переменными;
б) выявить парную связь между переменными;
в) выявить чистую связь между переменными;
г) элиминировать наведенные связи между переменными.
2. Напишите
систему нормальных уравнений для
определения
-коэффициентов
для уравнения
множественной регрессии
в стандартизованном виде с включением
двух факторов.
3. Поле корреляции в линейных моделях имеет вид: B
4. Наличие автокорреляции остатков можно определить используя:
А) критерий Стьюдента; Б) критерий Фишера; В) критерий Чоу; Г) критерий Энгеля-Грангера;
Д) критерий Спирмена; Е) критерий Дарбина-Уотсона.
5. Парный линейный коэффициент корреляции характеризует наличие слабой обратной связи, значит он принимает следующее значение: Д
а)1,2; б) -0,82; в) 0,23; г) 0,92; д)-0,24
6. Коэффициент уравнения парной регрессии показывает:
а) тесноту связи между зависимой и независимой переменными;
б) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на единицу;
в) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%;
г) на сколько ед. изменится зависимая переменная, если независимая переменная изменится на 1 ед.
7. Для двух видов продукции А и В модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
Определите, каким должен быть объем выпускаемой продукции, чтобы коэффициенты эластичности для продукции А и В были равны.
Что характеризует
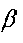-коэффициент
в уравнениях множественной регрессии?d-критерий Фишера используется для оценки: А)Наличия коинтеграции временных рядов.
Б) Наличия коинтеграции рядов распределения.
В) Автокорреляции остатков.
Г) Автокорреляции уровней рядов динамики.
Д) Автокорреляции уровней рядов распределения.
Вариант XVII
1. Эластичность уравнения парной линейной регрессии показывает:
а) тесноту связи между зависимой и независимой переменными;
б) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на единицу;
в) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%;
г) на сколько ед. изменится зависимая переменная, если независимая переменная изменится на 1 ед.
2. Поле корреляции в степенных моделях имеет вид: (а)
признак?
Г) вывод сделать
невозможно.
4. Степень влияния неучтенных факторов в рассматриваемой модели можно определить на основе: а) парного линейного коэффициента корреляции;
Б) частного коэффициента корреляции;
В) индекса корреляции;
Г) коэффициента детерминации;
Д) коэффициента регрессии;
Е) нет правильного ответа (дисперсионный анализ)
5 . В однофакторном дисперсионном анализе общую дисперсию можно разложить на следующие дисперсии:
