Вариант I
1. Коэффициент уравнения парной регрессии показывает:
а) тесноту связи между зависимой и независимой переменными;
б) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на единицу;
в) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%;
г) на сколько ед. изменится зависимая переменная, если независимая переменная изменится на 1 ед.
2. Поле корреляции в степенных моделях имеет вид: (А)
Б) коэффициента автокорреляции;
В) критерия Стьюдента;
Г) критерия Энгеля-Грангера;
Д) критерия Дарбина-Уотсона.
4. Степень влияния неучтенных факторов в рассматриваемой модели можно определить на основе: А) парного линейного коэффициента корреляции;
Б) частного коэффициента корреляции;
В) индекса корреляции;
Г) коэффициента детерминации;
Д) коэффициента регрессии;
Е) нет правильного ответа (дисперсионный анализ)
5 . Частный критерий Фишера вычисляется по формуле: (Г)
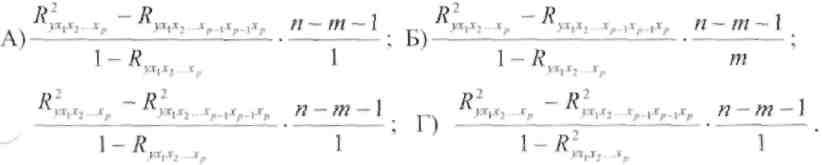
Постройте систему нормальных уравнений для линейной модели.Что характеризует свободный член линейного уравнения регрессии?
Уравнение множественной регрессии в стандартизованном виде имеет вид:
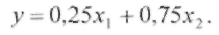Сила влияния, какого фактора выше на
результативный признак? (А)
9. Матрица парных линейных коэффициентов корреляции имеет вид:
Постройте уравнение
регрессии в стандартизованном виде.
1. Оценить значимость парного линейного коэффициента регрессии в парной линейной модели можно при помощи:
А) коэффициента корреляции;
Б) коэффициента автокорреляции;
В) критерия Стьюдента;
Г) критерия Энгеля-Грангера;
Д) критерия Дарбина-Уотсона.
2. Парный линейный коэффициент корреляции определяется по формуле: (скорее А, чем В)
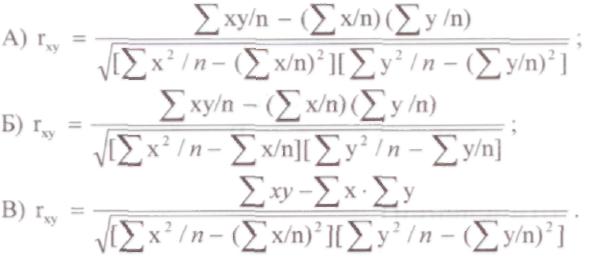
Изложите алгоритм использования критерия Дарбина-Уотсона.
4. Степень усредненного влияния неучтенных факторов в рассматриваемой модели можно определить на основе:
А) парного линейного коэффициента корреляции; Б) частного коэффициента корреляции;
В) индекса корреляции;
Г) коэффициента детерминации;
Д) коэффициента регрессии;
Е) свободного члена уравнения регрессии (???);
Ж) нет правильного ответа.
5 . Как вычисляется коэффициент эластичности для параболы II порядка? (Таблица, что скинул антон)
6. Общая дисперсия вычисляется по формуле: (Е)
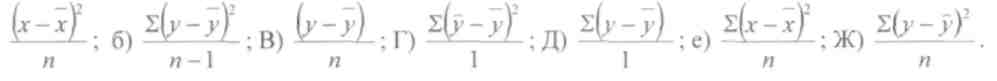
Что характеризует F-критерий Фишера? Данный к-т позволяет определить при каких значениях к-та детерминации уравнение регрессии следует считать статистически значимым, и когда оно обосновано при использовании в регрессионном анализе.Уравнение множественной регрессии в стандартизованном виде имеет вид: у = 0,5х1+ 0,5х2 .
Сила влияния какого фактора выше на результативный признак?
