27. Економічна і математична постановка цілочислової задачі лінійного програмування

Існує доволі широке коло задач математичного програмування, в економіко-математичних моделях яких одна або кілька змінних мають набувати цілих значень. Наприклад, коли йдеться про кількість верстатів у цеху, тварин у сільськогосподарських підприємствах тощо.

Зустрічаються також задачі, які з першого погляду не мають нічого спільного з цілочисловими моделями, проте формулюються як задачі цілочислового програмування. Вимоги дискретності змінних в явній чи неявній формах притаманні таким практичним задачам, як вибір послідовності виробничих процесів; календарне планування роботи підприємства; планування та забезпечення матеріально-технічного постачання, розміщення підприємств, розподіл капіталовкладень, планування використання обладнання тощо.

Задача математичного програмування, змінні якої мають набувати цілих значень, називається задачею цілочислового програмування. У тому разі, коли цілочислових значень мають набувати не всі, а одна чи кілька змінних, задача називається частково цілочисловою.

До цілочислового програмування належать також ті задачі оптимізації, в яких змінні набувають лише двох значень: 0 або 1 (бульові, або бінарні змінні).

Умова цілочисловості є по суті нелінійною і може зустрічатися в задачах, що містять як лінійні, так і нелінійні функції. Розглянемо задачі математичного програмування, в яких крім умови цілочисловості всі обмеження та цільова функція є лінійними, що мають назву цілочислових задач лінійного програмування.

Загальна цілочислова задача лінійного програмування записується так:

(8.1)

за умов:

; (8.2)

; (8.3)

– цілі числа . (8.4)

28. Геометрична інтерпретація розв’язків цілочислових задач лінійного програмування на площині

Для знаходження оптимального розв’язку цілочислових задач застосовують спеціальні методи. Найпростішим з них є знаходження оптимального розв’язку задачі як такої, що має лише неперервні змінні, з дальшим їх округленням. Такий підхід є виправ­даним тоді, коли змінні в оптимальному плані набувають досить великих значень у зіставленні їх з одиницями вимірювання. Нехай, наприклад, у результаті розв’язування задачі про поєднання галузей у сільськогосподарському підприємстві отримали оптимальне поголів’я корів – 1235,6. Округливши це значення до 1236, не припустимося значної похибки. Проте за деяких умов такі спрощення призводять до істотних неточностей. Скажімо, множина допустимих розв’язків деякої нецілочислової задачі лінійного програмування має вигляд, зображений на рис.8.1.

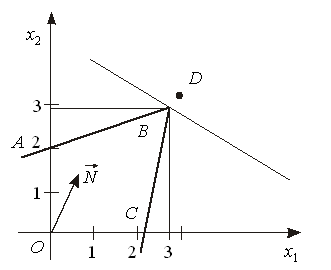
Рисунок 8.1

Максимальне значення функ­ціонала для даної задачі знаходиться в точці В. Округлення дасть таке значення оптимального плану (точка D на рис.8.1). Очевидно, що точка D не може бути розв’язком задачі, оскільки вона навіть не належить множині допустимих роз­в’язків (чотирикутник ОАВС), тобто відповідні значення змінних не задовольнятимуть систему обмежень задачі.

Зауважимо, що геометрично множина допустимих планів будь-якої лінійної цілочислової задачі являє собою систему точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної нецілочислової задачі. Отже, для розглянутого на рис.8.1 випадку множина допустимих планів складається з дев’яти точок (рис.8.2), які утворені перетинами сім’ї прямих, що паралельні осям Ох₁ та Oх₂ і проходять через точки з цілими координатами 0, 1, 2.

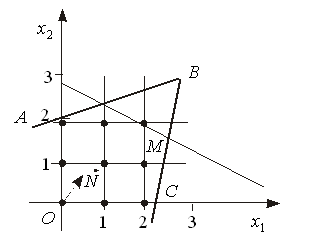
Рисунок 8.2

Для знаходження цілочислового оптимального розв’язку пряму, що відповідає цільовій функції, пересуваємо у напрямку вектора нормалі до перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний цілочисловий розв’я­зок відповідає точці М ( ).

Очевидно, особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисловості розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок. Якщо у разі двох змінних розв’язок задачі можна відшукати графічним методом, тобто, використовуючи цілочислову сітку, можна досить просто знайти оптимальний план, то в іншому разі необхідно застосовувати спеціальні методи.

8.3 Загальна характеристика методів розв’язування цілочислових задач лінійного програмування

Для знаходження оптимальних планів задач цілочислового програмування застосовують такі групи методів:

1) точні методи:

• методи відтинання;

• комбінаторні методи;

2) наближені методи.

Основою методів відтинання є ідея поступового «звуження» області допустимих розв’язків розглядуваної задачі. Пошук цілочислового оптимуму починається з розв’язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисловості змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисловість змінних, багатогранник допустимих розв’язків послабленої задачі поступово зменшують доти, доки змінні оптимального розв’язку не набудуть цілочислових значень.

До цієї групи належать:

а) методи розв’язування повністю цілочислових задач (дробовий алгоритм Гоморі);

б) методи розв’язування частково цілочислових задач (другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).

Комбінаторні методи цілочислової оптимізації базуються на ідеї перебору всіх допустимих цілочислових розв’язків, однак, згідно з їх процедурою здійснюється цілеспрямований перебір лише досить невеликої частини розв’язків.

Найпоширенішим у цій групі методів є метод гілок і меж.

Починаючи з розв’язування послабленої задачі, він передбачає поділ початкової задачі на дві підзадачі через виключення областей, що не мають цілочислових розв’язків, і дослідження кожної окремої частини багатогранника допустимих розв’язків.

Для розв’язування задач із бульовими змінними застосовують комбінаторні методи, причому, оскільки змінні є бульовими, то методи пошуку оптимуму значно спрощуються.

Досить поширеними є також наближені методи розв’язування цілочислових задач лінійного програмування. Оскільки для практичних задач великої розмірності за допомогою точних методів не завжди можна знайти строго оптимальний розв’язок за прий­нятний час або для розв’язування задачі використовуються наближено визначені, неточні початкові дані, то часто в реальних задачах досить обмежитися наближеним розв’язком, пошук якого є спрощеним.

Значна частина наближених алгоритмів базується на використанні обчислювальних схем відомих точних методів, таких, наприклад, як метод гілок і меж.

До наближених методів належать: метод локальної оптимізації (метод вектора спаду); модифікації точних методів; методи випадкового пошуку та ін.

Головними показниками для зіставлення ефективності застосування конкретних наближених алгоритмів на практиці є такі: абсолютна та відносна похибки отриманих наближених розв’язків.

, ,

де F – цільова функція (в даному разі для визначеності допускаємо вимогу відшукання максимального її значення); Х₁ –наближений розв’язок, знайдений деяким наближеним методом; Х^* – оптимальний план задачі.