25. Постановка и типы транспортных задач.

Простейшими транспортными задачами являются задачи о перевозках некоторого однородного груза из пунктов отправления (от поставщиков) в пункты назначения (к потребителям при обеспечении минимальных затрат на перевозки).

Рассмотрим такую задачу.

Имеется поставщиков А_i и n потребителей . Количество груза, находящегося у поставщика , будем обозначать через . Количество груза, необходимое потребителю - через . Дана матрица тарифов (издержек или транспортных расходов).

где с_ij= стоимость перевозки единицы груза от i-го поставщика к j-му потребителю.

Планом транспортной задачи называется матрица

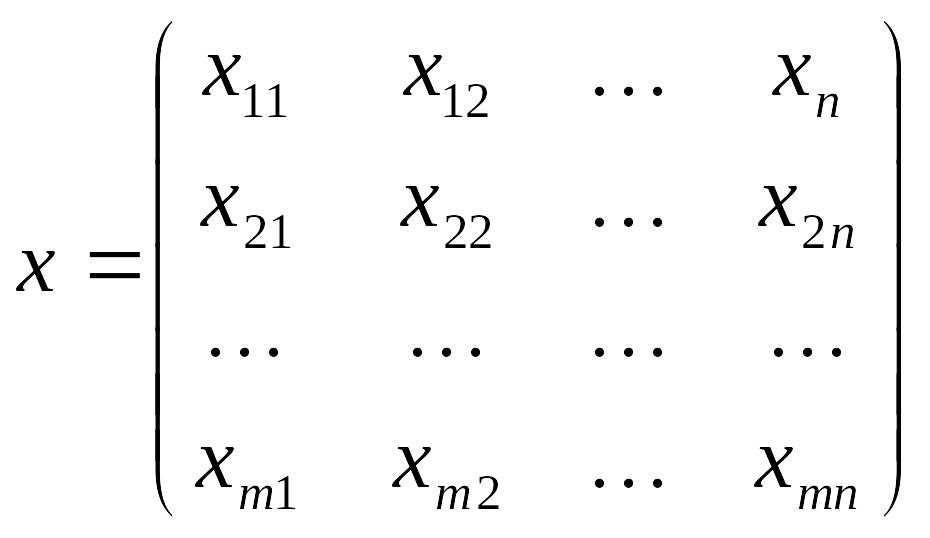
Где x_ij обозначает количество груза, которое надо доставить от i-го поставщика к j-му потребителю.

Общие суммарные затраты, связанные с реализацией плана перевозок, модно представить целевой функцией:

Математическая модель задачи выглядит так:

Система ограничений содержит m+n уравнений переменными.

Если суммарный объем груза поставщиков равен суммарному спросу потребителей, то есть

то это транспортная задача с закрытой моделью.

А если , то это транспортная задача с открытой моделью.

Равенство является необходимым и достаточным условием совместности ограничений задачи.

Для транспортной задачи важное значение имеет теорема о ранге матрицы.

Теорема.

Ранаг матрицы транспортной задачи на единицу меньше уровней, то есть

С учетом этой теоремы в каждой матрице перевозок опорный план должен содержать не более занятых клеток, а остальные –свободные.

26. Методы построения начального опорного решения.

1. Метод северо-западного угла.

Существует ряд методов построения начального опорного решения, наиболее простым из которых является метод северо-западного угла. В данном методе запасы очередного поставщика используется для обеспечения запросов очередных потребителей до тих пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.

Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запасов очередного потребителя, заполняется только одна клетка и, соответственно, исключается из рассмотрения один поставщик или потребитель.

2. Метод минимального элемента (минимальной стоимости).

Метод минимальной стоимости прост, он позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи Как и метод северо-западного угла, он состоит из ряда однотипних шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости , и исключаетсч из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую , заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы использованы полностью. Потребитель исключается из рассмотрения, если его запасы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулюЮ то на том шаге, корда от данного постащика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лиш затем поставщик исключается из рассмотрения. Аналогично с потребителем.

Пример:

Имеется три поставщика А₁,А₂ и А₃, а так же четыре потребителя В₁,В₂,В₃ и В₄. Количество груза, находящегося у поставщика, равно соответственно: Количество груза, необходимого потребителю В_j, равно соответственно: Данаматрица тарифов (издержек или транспортных расходов):

Решение:

Так как то данная задача – закрытого типа. Составим первоначальный опорный план двумя различными способами.

1. Способ северо-западного угла

Таблица 4.7

	В1	В2	В3	В4
A1	5	4	1	2
	40	20	-	-	60,20,0
A2	4	2	6	3
	-	5	20	15	40,35,15
A3	7	3	5	4
	-	-	-	35	35,0
bj	40,0	25,5,0	20,0	50,35.0

X=

F=5*40+4*20+2*5+6*20+3*15+4*35=595(y.d.e)

2. Способ минимального элемента.

Таблица 4.8

	В1	В2	В3	В4
A1	5	4	1	2
	-	-	20	40	60,40,0
A2	4	2	6	3
	5	25	-	10	40,15,5
A3	7	3	5	4
	35	-	-	-	35,0
bj	40,35,0	25,0	20,0	50,10,0

X=

F=1*20+2*40+4*5+2*25+3*10+7*35=445(y.d.e)

Таким образом, опорный план, найденный способом минимального элемента, ближе к оптимальному, чем план, найденный способом северо-западного угла.