
- •1. Сутність моделювання як методу наукового пізнання.
- •2 Особливості та принципи математичного моделювання.
- •3. Основні дефініції економіко-математичного моделювання.
- •4. Особливості економічних спостережень і вимірів.
- •5. Етапи економіко-математичного моделювання.
- •6. Елементи класифікації економіко-математичних моделей.
- •7. Роль прикладних економіко-математичних досліджень.
- •8. «Павутиноподібна» модель ринку
- •9. Постановка задачі економіко-математичного моделювання.
- •10. Приклади задач економіко-математичного моделювання (самостійна робота) .
- •11. Загальна економіко-математична модель задачі лінійного програмування
- •12. Форми запису задач лінійного програмування
- •13. Геометрична інтерпретація задачі лінійного програмування
- •14. Основні властивості розв’язків задачі лінійного програмування
- •15. Графічний метод розв’язування задач лінійного програмування
- •16. Початковий опорний план.
- •17. Перехід від одного опорного плану до іншого.
- •18. Оптимальний розв’язок. Критерій оптимальності плану.
- •19. Розв’язування задачі лінійного програмування симплексним методом.
- •20. Метод штучного базису.
- •21. Економічна інтерпретація прямої та двоїстої задач лінійного програмування.
- •22. Правила побудови двоїстих задач.
- •23. Основні теореми двоїстості та їх економічний зміст.
- •24. Приклади застосування теорії двоїстості для знаходження оптимальних планів прямої та двоїстої задач.
- •25. Постановка и типы транспортных задач.
- •26. Методы построения начального опорного решения.
- •1. Метод северо-западного угла.
- •2. Метод минимального элемента (минимальной стоимости).
- •27. Економічна і математична постановка цілочислової задачі лінійного програмування
- •28. Геометрична інтерпретація розв’язків цілочислових задач лінійного програмування на площині
- •29. Методи відтинання. Метод Гоморі
- •30. Комбінаторні методи. Метод гілок та меж
- •31. Економічна і математична постановка задачі нелінійного програмування
- •32. Геометрична інтерпретація задачі нелінійного програмування
- •33. Основні труднощі розв’язування задач нелінійного програмування
- •34. Класичний метод оптимізації. Метод множників Лагранжа
- •35. Необхідні умови існування сідлової точки
18. Оптимальний розв’язок. Критерій оптимальності плану.
Розглянемо, як, виходячи з початкового опорного плану (4.6), перейти до наступного опорного плану, що відповідає цілеспрямованому процесу перебору кутових точок багатогранника розв’язків.
Оскільки є базисом m-вимірного простору, то кожен з векторів співвідношення (4.5) може бути розкладений за цими векторами базису, причому у єдиний спосіб:
Розглянемо такий розклад для довільного небазисного вектора, наприклад, для :
(4.7)
Припустимо, що у виразі (4.7) існує хоча б один додатний коефіцієнт .
Введемо деяку поки що невідому величину , помножимо на неї обидві частини рівності (4.7) і віднімемо результат з рівності (4.6). Отримаємо:
(4.8)
Отже, вектор
є планом задачі у тому разі, якщо його компоненти невід’ємні. За допущенням , отже, ті компоненти вектора , в які входять , будуть невід’ємними, тому необхідно розглядати лише ті компоненти, які містять додатні . Тобто необхідно знайти таке значення , за якого для всіх буде виконуватися умова невід’ємності плану задачі:
(4.9)
З (4.9) отримуємо, що для шуканого має виконуватися умова . Отже, вектор буде планом задачі для будь-якого , що задовольняє умову:
,
де мінімум знаходимо для тих i, для яких .
Опорний план не може містити більше ніж m додатних компонент, тому в плані необхідно перетворити в нуль хоча б одну з компонент. Допустимо, що для деякого значення і, тоді відповідна компонента плану перетвориться в нуль. Нехай це буде перша компонента плану, тобто:
.
Підставимо значення у вираз (4.8):
,
якщо позначити , , то рівняння можна подати у вигляді:
,
якому відповідає такий опорний план:
.
Для визначення наступного опорного плану необхідно аналогічно продовжити процес: будь-який вектор, що не входить у базис, розкласти за базисними векторами, а потім визначити таке , для якого один з векторів виключається з базису.
Отже, узагальнюючи розглянутий процес, можемо висновувати: визначення нових опорних планів полягає у виборі вектора, який слід ввести в базис, і вектора, який необхідно вивести з базису. Така процедура відповідає переходу від одного базису до іншого за допомогою методу Жордана-Гаусса.
Необхідно зазначити, що для випадку, коли вектор підлягає включенню в базис, а в його розкладі (4.7) всі , то, очевидно, не існує такого значення , яке виключало б один з векторів. У такому разі план містить m+1 додатних компонент, отже, система векторів буде лінійно залежною і визначає не кутову точку багатогранника розв’язків. Функціонал не може в ній набирати максимального значення. Це означає, що функціонал є необмеженим на багатограннику розв’язків.
19. Розв’язування задачі лінійного програмування симплексним методом.
![]()
![]() .
.
Перша симплексна таблиця для розв’язку задач лінійного програмування
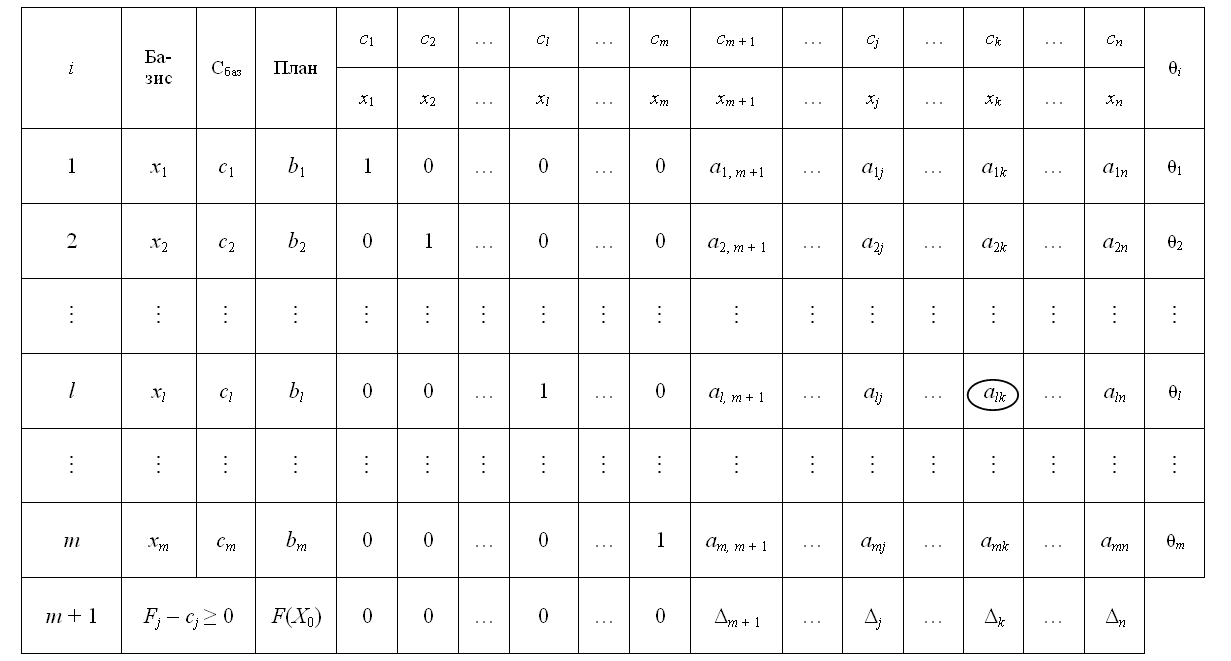
Після
заповнення табл.4.1
розраховують значення оцінок плану
(останній рядок):
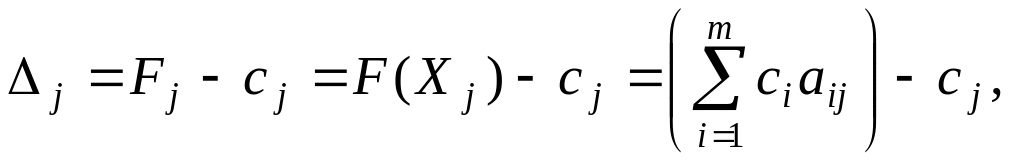
![]() .
Потім згідно з умовою оптимальності
плану задачі лінійного програмування,
якщо всі
.
Потім згідно з умовою оптимальності
плану задачі лінійного програмування,
якщо всі
![]() (для задачі на максимум), то план є
оптимальним. Допустимо, що одна з оцінок
(для задачі на максимум), то план є
оптимальним. Допустимо, що одна з оцінок
![]() ,
тоді план
не є оптимальним і необхідно здійснити
перехід до наступного опорного плану,
якому буде відповідати більше значення
функціонала. Якщо від’ємних оцінок
кілька, то включенню до базису підлягає
вектор, який вибирається як
,
тоді план
не є оптимальним і необхідно здійснити
перехід до наступного опорного плану,
якому буде відповідати більше значення
функціонала. Якщо від’ємних оцінок
кілька, то включенню до базису підлягає
вектор, який вибирається як
![]() .
Мінімум знаходять для тих індексів j,
де
.
Якщо існує кілька однакових значень
оцінок, що відповідають
,
то з відповідних їм векторів до базису
включають той, якому відповідає
максимальне значення функціонала.
.
Мінімум знаходять для тих індексів j,
де
.
Якщо існує кілька однакових значень
оцінок, що відповідають
,
то з відповідних їм векторів до базису
включають той, якому відповідає
максимальне значення функціонала.
Якщо
хоча б для однієї від’ємної оцінки
всі коефіцієнти розкладу
![]() відповідного вектора недодатні, то це
означає, що функціонал є необмеженим
на багатограннику розв’язків, тобто
багатогранник у даному разі являє собою
необмежену область і розв’язком задачі
є
відповідного вектора недодатні, то це
означає, що функціонал є необмеженим
на багатограннику розв’язків, тобто
багатогранник у даному разі являє собою
необмежену область і розв’язком задачі
є
![]() .
.
Нехай
![]() ,
тобто мінімальне значення досягається
для k-го
вектора
,
тобто мінімальне значення досягається
для k-го
вектора
![]() .
Тоді до базису включається вектор
.
Тоді до базису включається вектор
![]() .
Відповідний стовпчик симплексної
таблиці називають напрямним.
.
Відповідний стовпчик симплексної
таблиці називають напрямним.
Для того,
щоб вибрати вектор, який необхідно
вивести з базису (згідно з процедурою
переходу від одного опорного плану
задачі до іншого –
п.4.2),
розраховують останній стовпчик табл.4.1
–
значення
![]() .
.
![]() .
.
З
розрахованих значень необхідно вибрати
найменше
![]() .
Тоді з базису виключають i-ий
вектор, якому відповідає
.
.
Тоді з базису виключають i-ий
вектор, якому відповідає
.
Допустимо,
що
![]() відповідає вектору, що знаходиться в
l-му
рядку табл.4.1. Відповідний рядок
симплексної таблиці називають напрямним.
відповідає вектору, що знаходиться в
l-му
рядку табл.4.1. Відповідний рядок
симплексної таблиці називають напрямним.
![]() (4.16)
(4.16)
Вектор Аl виходить з базису, і його розклад за новим базисом отримаємо з виразу (4.16):
![]() . (4.17)
. (4.17)
Розклад вектора А0 за початковим базисом має вигляд:
![]() . (4.18)
. (4.18)
Для запису розкладу вектора в новому базисі підставимо вираз (4.17) у рівняння (4.18), маємо:
![]()
![]() Отже, значення
компонент наступного опорного плану
розраховуються за формулами:
Отже, значення
компонент наступного опорного плану
розраховуються за формулами:
![]() (4.19)
(4.19)
Розклад за початковим базисом будь-якого з векторів має вигляд:
![]() . (4.20)
. (4.20)
Розклад за новим базисом отримаємо підстановкою (4.17) у (4.20):
![]()
![]()
![]() .
.
Новий
план:
![]() ,
де
,
де
![]()
Друга симплексна таблиця для відшукання опорного (оптимального) плану
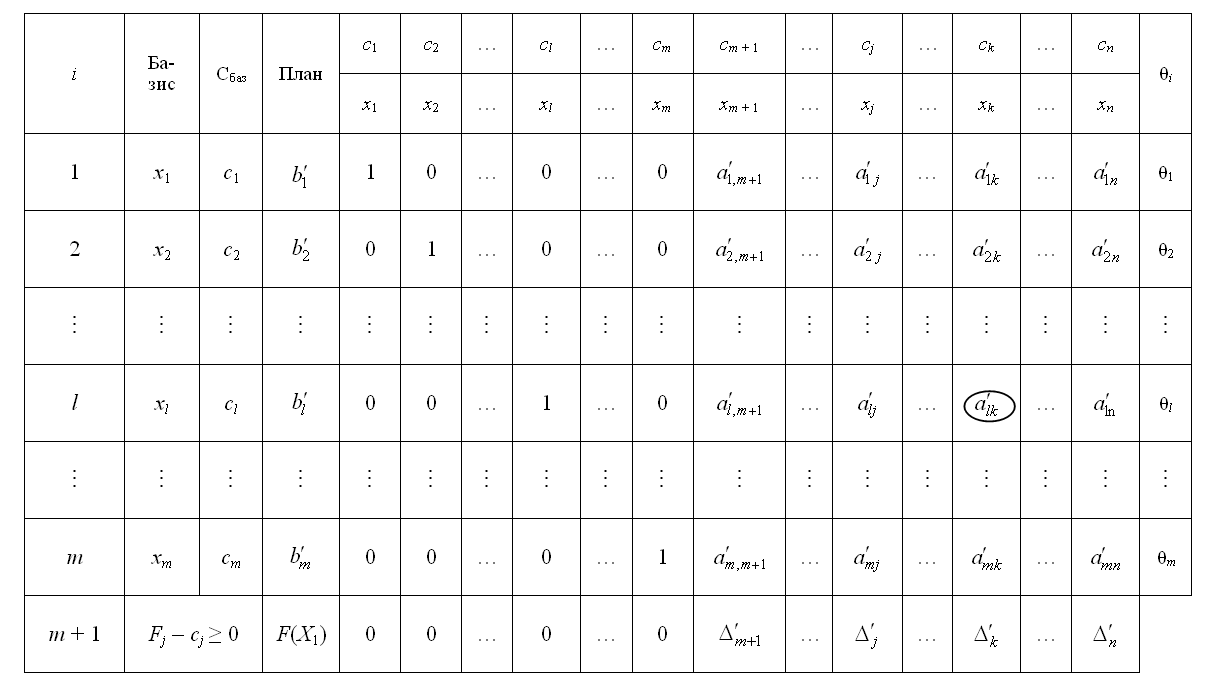
![]()
![]()
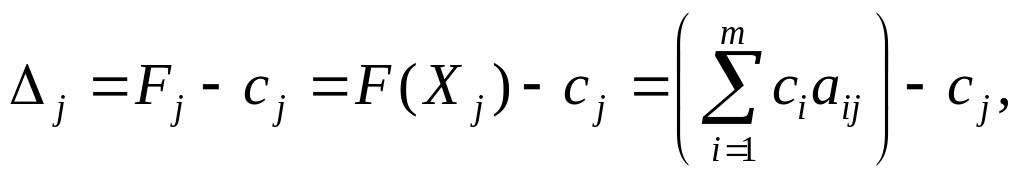
![]()
