29. Нахождение точки пересечения прямой и плоскости

Возможны три варианта взаимного расположения прямой и плоскости в пространстве:

• прямая лежит в плоскости;

• прямая параллельна плоскости;

• прямая пересекает плоскость.

Нас интересует третий случай. Напомним, что означает фраза: «прямая и плоскость пересекаются». Говорят, что прямая и плоскость пересекаются, если они имеют только одну общую точку. Это общую точку пересекающихся прямой и плоскости называют точкой пересечения прямой и плоскости.

Приведем графическую иллюстрацию.

К началу страницы

Нахождение координат точки пересечения прямой и плоскости.

Введем в трехмерном пространстве прямоугольную систему координат Oxyz. Теперь каждой прямой соответствуют уравнения прямой некоторого вида (им посвящена статья виды уравнений прямой в пространстве), каждой плоскости отвечает уравнение плоскости (можете ознакомиться со статьей виды уравнения плоскости), а каждой точке соответствует упорядоченная тройка чисел – координаты точки. Дальнейшее изложение подразумевает знание всех видов уравнений прямой в пространстве и всех видов уравнения плоскости, а также умение переходить от одного вида уравнений к другому виду. Но не пугайтесь, по тексту мы будем приводить ссылки на необходимую теорию.

Давайте сначала детально разберем задачу, решение которой мы можем получить на основании определения точки пересечения прямой и плоскости. Эта задача нас подготовит к нахождению координат точки пересечения прямой и плоскости.

Пример.

Является ли точка М₀ с координатами   точкой пересечения прямой   и плоскости  .

Решение.

Нам известно, что если точка принадлежит некоторой прямой, то координаты точки удовлетворяют уравнениям прямой. Аналогично, если точка лежит в некоторой плоскости, то координаты точки удовлетворяют уравнению этой плоскости. По определению точка пересечения прямой и плоскости является общей точкой прямой и плоскости, тогда координаты точки пересечения удовлетворяют как уравнениям прямой, так и уравнению плоскости.

Таким образом, для решения поставленной задачи нам следует подставить координаты точки М₀ в заданные уравнения прямой и в уравнение плоскости. Если при этом все уравнения обратятся в верные равенства, то точка М₀ является точкой пересечения заданных прямой и плоскости, в противном случае точка М₀ не является точкой пересечения прямой и плоскости.

Подставляем координаты точки  :

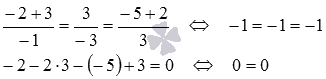
Все уравнения обратились в верные равенства, следовательно, точка М₀ принадлежит одновременно и прямой   и плоскости  , то есть, М₀является точкой пересечения указанных прямой и плоскости.

Ответ:

да, точка   - это точка пересечения прямой   и плоскости  .

Итак, координаты точки пересечения прямой и плоскости удовлетворяют как уравнениям прямой, так и уравнению плоскости. Этим фактом и будем пользоваться при нахождении координат точки пересечения прямой и плоскости.

Первый способ нахождения координат точки пересечения прямой и плоскости.

Пусть в прямоугольной системе координат Oxyz заданы прямая a и плоскость  , причем известно, что прямая a и плоскость   пересекаются в точке М₀.

Найдем координаты точки М₀ для случая, когда плоскость   задана общим уравнением плоскости вида  , а прямая а является линией пересечения двух плоскостей   и   (такому способу задания прямой линии в пространстве посвящена статья уравнения прямой - уравнения двух пересекающихся плоскостей).

Искомые координаты точки пересечения прямой a и плоскости  , как мы уже говорили, удовлетворяют и уравнениям прямой a, и уравнению плоскости  , следовательно, они могут быть найдены как решение системы линейных уравнений вида  . Это действительно так, так как решение системы линейных уравнений обращает каждое уравнение системы в тождество.

Отметим, что при такой постановке задачи мы фактически находим координаты точки пересечения трех плоскостей, заданных уравнениями  ,   и  .

Решим пример для закрепления материала.

Пример.

Прямая, заданная уравнениями двух пересекающихся плоскостей как  , пересекает плоскость  . Найдите координаты точки пересечения прямой и плоскости.

Решение.

Требуемые координаты точки пересечения прямой и плоскости мы получим, решив систему уравнений вида 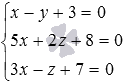 . При этом будем опираться на информацию статьи решение систем линейных уравнений.

Для начала перепишем систему уравнений в виде   и вычислим определитель основной матрицы системы (при необходимости обращайтесь к статьевычисление определителя матрицы):

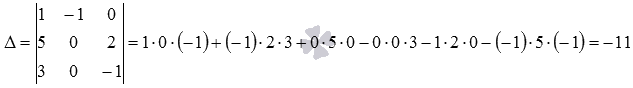
Определитель основной матрицы системы отличен от нуля, поэтому система уравнений имеет единственное решение. Для его отыскания можно воспользоваться любым методом. Мы используем метод Крамера:

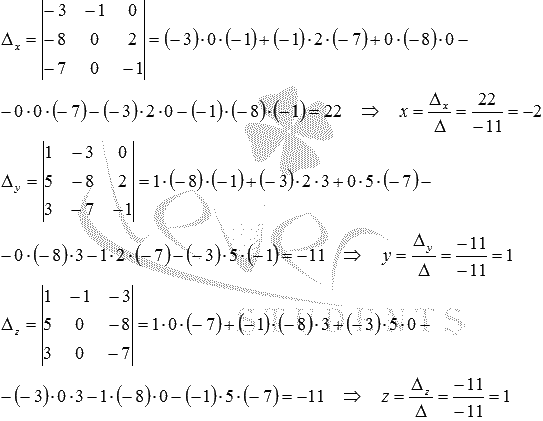
Так мы получили координаты точки пересечения прямой и плоскости (-2, 1, 1).

Ответ:

(-2, 1, 1).

Следует отметить, что система уравнений   имеет единственное решение, если прямая a, определенная уравнениями  , и плоскость  , заданная уравнением  , пересекаются. Если прямая a лежит в плоскости  , то система имеет бесконечное множество решений. Если же прямая aпараллельна плоскости  , то система уравнений решений не имеет.

Пример.

Найдите точку пересечения прямо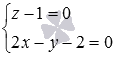й   и плоскости  , если это возможно.

Решение.

Оговорка «если это возможно» означает, что прямая и плоскость могут не пересекаться.

Составим систему из заданных уравнений 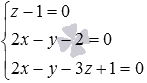 . Если эта система уравнений имеет единственное решение, то оно даст нам искомые координаты точки пересечения прямой и плоскости. Если эта система не имеет решений или имеет бесконечно много решений, то о нахождении координат точки пересечения не может быть и речи, так как прямая либо параллельна плоскости, либо лежит в этой плоскости.

Основная матрица системы имеет вид 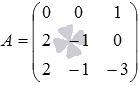 , а расширенная матрица - 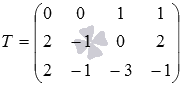 . Определим ранг матрицы А и ранг матрицы Т методом окаймляющих миноров:  . То есть, ранг основной матрицы равен рангу расширенной матрицы системы и равен двум. Следовательно, на основании теоремы Кронекера-Капелли можно утверждать, что система уравнений имеет бесконечное множество решений.

Таким образом, прямая   лежит в плоскости  , и мы не можем говорить о нахождении координат точки пересечения прямой и плоскости.

Ответ:

невозможно найти координаты точки пересечения прямой и плоскости.

Пример.

Если прямая   пересекается с плоскостью  , то найдите координаты точки их пересечения.

Решение.

Составим систему из заданных уравнений 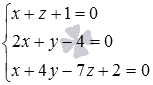 . Для нахождения ее решения используем метод Гаусса. Метод Гаусса позволит нам не только определить, имеет ли записанная система уравнений одно решение, бесконечное множество решений или не имеет ни одного решения, но и найти решения в случае их наличия.

Последнее уравнение системы после прямого хода метода Гаусса стало неверным равенством, следовательно, система уравнений не имеет решений. Отсюда заключаем, что прямая   и плоскость   не имеют общих точек. Таким образом, мы не можем говорить о нахождении координат их точки пересечения.

Ответ:

прямая параллельна плоскости и они не имеют точки пересечения.

Заметим, что если прямой a соответствуют параметрические уравнения прямой в пространствеили канонические уравнения прямой в пространстве, то можно получить уравнения двух пересекающихся плоскостей, определяющих прямую a, и после этого находить координаты точки пересечения прямой a и плоскости   разобранным способом. Однако проще использовать другой метод, к описанию которого мы и переходим.

Второй способ нахождения координат точки пересечения прямой и плоскости.

Пусть в прямоугольной системе координат Oxyz прямая a пересекает плоскость   в точке М₀. Найдем координаты точки М₀ для случая, когда плоскость   задана общим уравнением плоскости вида  , а прямая а определена параметрическими уравнениями вида  .

Если в уравнение   подставить выражения  , мы придем к уравнению с неизвестной  . Разрешив это уравнение относительно  , мы получим значение  , соответствующее координатам точки пересечения прямой a и плоскости  . Координаты точки пересечения прямой и плоскости вычисляются как  .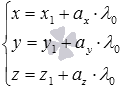

Разберем этот способ нахождения координат точки пересечения прямой и плоскости на примере.

Пример.

Найдите координаты точки пересечения прямой   и плоскости  .

Решение.

Подставим в уравнение плоскости выражения  :

Находим координаты точки пересечения прямой и плоскости по параметрическим уравнениям при  :

Ответ:

(3, 0, -1).

Обратите внимание: если прямая   лежит в плоскости  , то, подставив в уравнение   выражения  , мы получим тождество  , а если указанная прямая параллельна плоскости - то мы получим неверное равенство.

В заключении скажем про случай, когда прямая a задана каноническими уравнениями вида  . В этом случае для нахождения координат точки пересечения прямойa с плоскостью  , от канонических уравнений прямой следует перейти к параметрическим уравнениям этой прямой ( ) и воспользоваться разобранным способом.