25. Уравнение плоскости, проходящей через 3 точки(получить).Примеры.

Через 3 точки можно провести плоскость,при том только одну (аксиома геометрии).

т.М1 (x1;y1;z1)

т.M2 (x2;y2;z2)

т.M3 (x3;y3;z3) Рассмотрим т.М (x;y;z)

M1M , M1M2 , M1M3 –компланарны,при любом положении т.M

т.к. вектора компланарны : M1M*M1M2*M1M3=0 (СМЕШАННОЕ ПРОИЗВЕДЕНИЕ)

M1M=(x-x1;y-y1;z-z1)

M1M2=(x2-x1;y2-y1;z2-z1)

M1M3=(x3-x1;y3-y1;z3-z1)

|x-x1 y-y1 z-z1 | |x2-x1 y2-y1 z2-z1| - Уравнение плоскости,проходящей через 3 заданные точки |x3-x1 y3-y1 z3-z1|

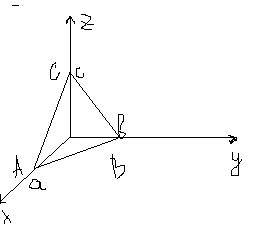
26. Получить уравнение плоскости в отрезках на осях

Найдем уравнения плоскости, проходящей через т.А,В,С. |x-a y z| A(a;0;0) |-a b 0 | = (x-a)b*c+(-y)*(-ac)+z*ab=0

B(0;b;0) |-a 0 c|

C(0;0;c)

Xbc-abc+yac+zab=0

Xbc+yac+zab=abc

a не равно 0;b не равно 0;с не равно нулю.

x/a+y/b+z/c=1-уравнение плоскости в отрезках на осях

27. Формула для вычисления расстояния от точки до плоскости, нахождение угла между плоскостями. Условия параллельности и перпендикулярности а) Формула

.

Строгая формулировка

Если плоскость задана уравнением  , то расстояние   от точки   до этой плоскости можно вычислить по формуле .

Б) УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Р ассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами   и   плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов   или  . Поэтому  . Т.к.  и  , то

.

Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

В) Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы   и   параллельны, а значит  .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или 

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно,  или  .

Таким образом,  .

28. Приведение обзих уравнений прямой в пространстве к каноническому виду

Существуют различные виды уравнения прямой на плоскости, описывающие одну и ту же линию. В зависимости от условий задачи удобно использовать тот или иной вид уравнения прямой. Поэтому, полезно уметь переходить от уравнения прямой одного вида к уравнению прямой другого вида. Цель этого пункта статьи заключается в приобретении навыков приведения общего уравнения прямой к другим видам уравнения прямой и обратно.

Начнем с приведения общего уравнения прямой   к каноническому уравнению прямой вида  .

Если  , то переносим слагаемое   в правую часть равенства   с противоположным знаком  . В левой части равенства выносим А за скобки 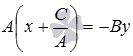 . Полученное равенство можно записать как пропорцию вида  .

Если  , то оставляем в левой части общего уравнения прямой   только слагаемое  , а остальные переносим в правую часть с противоположным знаком:  . Теперь выносим в правой части равенства –B за скобки 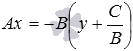  и записываем полученное равенство в виде пропорции  . Вот и все.

Запоминать полученные формулы не имеет смысла, проще повторять указанные действия при приведении общего уравнения прямой к каноническому виду.

Пример.

Приведите уравнение прямой   к каноническому виду.

Решение.

Исходное неполное уравнение прямой перепишем как  . Оставляем в левой части равенства только слагаемое  :  . В правой части равенства выносим -3 за скобки: 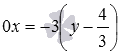 . Осталось записать полученное равенство в виде пропорции   и на этом приведение общего уравнения прямой к каноническому виду завершено.

Ответ: