Определение скалярного произведения векторов, свойства, в ортонормированном базисе Скалярное произведение векторов – число равное произведению длин этих векторов на косинус угла между ними
A*b= ax*bx + ay*by + az*bz
Свойства: 1) произведение суммы двух векторов равно сумме проекций; 2) при умножении вектора на число его проекция то же умножается на это число;
Определение векторного произведения векторов, свойства, в ортонормированном базисе
Векторное произведение векторов – вектор С, которое определяется тремя условиями: |c|=|a|*|b|*sinf ; с перпендикулярно в; а, б, с – правая тройка (упорядоченая тройка некомпланарных векторов называется правой, если после приведения их к общему началу, из конца третьего вектора, кратчайший поворот от первого ко второму виден в направлении противоположном направлению движения часовой стрелки)
Свойства: 1) a*b = -a*b; 2) ka *b = k(a*b); 3) a*0=0; 4) a(b*c)= ab + ac; 5) a*b=0 если a параллельно b
Смешанное произведение 3х векторов. Геометрический смысл, свойства, пример в ортонормированном базисе
Смешаное произведение трех векторов – это число, которое получается от умножения векторного произведения а*б скалярно на с
Геометрический смысл: результат смешанного произведения – это объем параллелепипеда, построенного на а, б, с
Условия ортогональности, коллинеарности и камплонарности
Условие
ортогональности: а
б
(с=а*б*Cosf)
cos90=0
ax*bx + ay*by + az*bz = 0
Деление отрезка в данном отношении, расстояние между двумя точками в R2 и R3
x
=
справедливо для y,
z
Померные координаты и их связь с декартовыми прямоугольными. Построение кривых в системе координат
Вывод уравнения прямой в плоскости проходящей через точку, перпендикулярно данному вектору
Получить общее уравнение прямой на плоскости и рассмотреть его частные случаи.
Получить уравнение прямой в отрезках на осях
Получить каноническое уравнение прямой на плоскости и в пространстве
Получить параметрическое уравнение прямой на плоскости и в пространстве
Поучить уравнение прямой проходящей через 2 точки на плоскости
Получить уравнение пучка прямых на плоскости и построение прямой с условным коэффициентом
Условие параллельности и перпендикулярности прямых на плоскости и в пространстве, формула расстояния от точки до прямой на плоскости
(L1)||
(L2)
если n1||n2
=
и k1=k2
– условие параллельности
(L1) ˫(L2) если n1 * n2 = 0; Cosf = 0; A1*A2 + B1*B2 = 0 и k1*k2=-1 – условие перпендикулярности
расстояние от
точки M
(
)
до прямой
Каноническое уравнение эллипсиса, эксцентриситет, разновидности эллипсиса, Каноническое уравнение гиперболы, асимптоты гиперболы, эксцентриситет гиперболы, разновидности
Каноническое уравнение эллипса
Эксцентриситет ὲ=с/a,если а главная полуось(т.е. на ней находится фокус), и ὲ=с/bесли b главная полуось.
Эксцентриситет у эллипса всегда меньше единицы т.к. с<a,b
Каноническое уравнение гиперболы
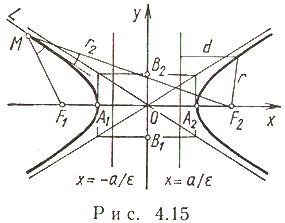
На рис 4.15.уравнение гиперболы с а-действительной полуосью и b мнимой полуосью, если b действительная полуось а а-мнимая полуось то график будет симметричен относительно оси ОX
Уравнения асимптот: для действительной полуоси аy=±a/b*x , для действительной полуоси by=±b/a*x
Аналогично, как и у эллипса,эксцентриситеты зависят от действительной оси гиперболы
ὲ=с/aесли а действительная полуось,и ὲ=c/b если b действительная полуось