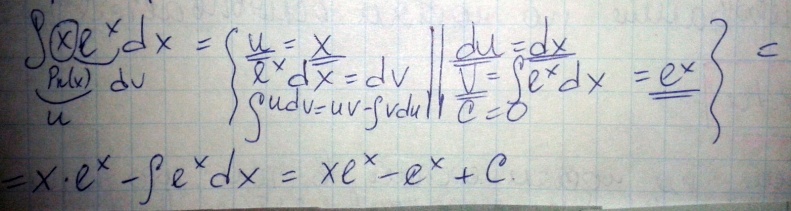- •Основные понятия, связанные с матрицами. Линейные операции над матрицами, умножение. Примеры
- •Обратная матрица, формула вычисления обратной матрицы. Примеры
- •Определители 3 и 2 порядка, определители n-го порядка. Свойства определителей, разложение определителя по элементам строки. Примеры
- •Метод Гаусса решения систем уравнений, примеры
- •Крамер.
- •Основные понятия связанные с векторами. Линейные операции в векторной и координатной форме
- •Определение скалярного произведения векторов, свойства, в ортонормированном базисе Скалярное произведение векторов – число равное произведению длин этих векторов на косинус угла между ними
- •Свойства: 1) произведение суммы двух векторов равно сумме проекций; 2) при умножении вектора на число его проекция то же умножается на это число;
- •Определение векторного произведения векторов, свойства, в ортонормированном базисе
- •Общее уравнение прямой второго порядка, окружность. Каноническое уравнение параболы, разновидности
- •Получить уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору.
- •Получить общее уравнение плоскости. Частные случаи
- •Уравнение плоскости, проходящей через 3 точки(получить).Примеры.
- •Получить уравнение плоскости в отрезках на осях
- •Формула для вычисления расстояния от точки до плоскости, нахождение угла между плоскостями. Условия параллельности и перпендикулярности а) Формула
- •Приведение обзих уравнений прямой в пространстве к каноническому виду
- •Нахождение точки пересечения прямой и плоскости
- •Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •Функции синус, косинус и их графики, производные
- •Функции тангенс, котангенс, свойства графики производные
- •Функции арккосинус, арксинус
- •Функции арктангенс, арккотангенс Функция arctg
- •Свойства функции arctg
- •Получение функции arctg
- •Функция arcctg
- •Свойства функции arcctg
- •Получение функции arcctg
- •Показательные функции, логарифмические, степенные их свойства, графики, производные Показательная функция
- •Определение показательной функции
- •Свойства
- •Логарифмическая функция
- •Свойства
- •Померные координаты и их связь с декартовыми прямоугольными. Построение кривых в системе координат
- •Вывод уравнения прямой в плоскости проходящей через точку, перпендикулярно данному вектору
- •Получить общее уравнение прямой на плоскости и рассмотреть его частные случаи.
- •Определение бесконечно малой:
- •Свойства бесконечно малой функции:
- •Теорема о связи между функцией и её пределом в точке (не уверен, но вроде вполне подходит!):
- •Определение бб и ее связь с бм.
- •Теорема о пределе суммы, произведений, частного, двух функций, предельные переходы в неравенствах
- •Сравнение бм и бб. Теорема о замене функций на эквивалентные при вычислении пределов. Два замечательных предела
- •Раскрытие неопределенностей ; ;
- •В) Неопределённость «бесконечность минус бесконечность» и «ноль умножить на беконечность»
- •Определение непрерывности функции в точке и на отрезке, классификация точек разрыва, теорема о непрерывности
- •Свойства функций непрерывных в точке и на отрезке
- •О пределение производной, геометрический и физический смысл, вывод уравнения касательной и нормали к кривой
- •Определение функции дифференцируемой в точке. Необходимое и достаточное условие дифференцируемости функции
- •Правила вычисления производных. Таблица производных различных функций
- •Диференциал функции одной переменной. Инвариантность формы диференциала.Диференциал постоянного; суммы; произведения; частного.
- •Теоремы Ролля, Коши, Лагранжа.
- •Правило Лапиталя, пример раскрытия неопределенности с помощью правила Лапиталя
- •Комплексные числа. Различные формы комплексных чисел. Арифметические действия
- •Формула Тейлора с остаточным членом в форме Лагранжа ( Пеано)
- •Монотонные функции на интервале. Необходимый и достаточный признак монотонности. Пример исследования на монотонность
- •Условия монотонности функции
- •Примеры
- •Точки локального максимума (минимума) необходимое условие локального экстремума функции. Первый и второй достаточный признак локального экстремума
- •Нахождение наибольшего и наименьшего значения непрерывной функции
- •Определение точки перегиба функции. Достаточное условие существования точек перегиба.
- •Определение асимптот графика функции. Виды асимптот
- •Определение первообразной. Теорема о множестве первообразных. Определение неопределенного интеграла. Основные свойства, таблица интегралов
- •Интегрирование методом замены переменной. Формула интегрирования по частям. Случаи ее применения
- •Интегрирование простейших дробей 1-3 типов
- •Вычисление интегралов типа:
- •Вычисление интегралов вида: * dx
- •Вычисление интегралов вида
Определение первообразной. Теорема о множестве первообразных. Определение неопределенного интеграла. Основные свойства, таблица интегралов
Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Неопределенным интегралом называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. или Функцию называют первообразной функции . Первообразная функции определяется с точностью до постоянной величины.
Напомним, что -дифференциал функции и определяется следующим образом:
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины.
![]()
![]()
![]()
![]()
Интегрирование методом замены переменной. Формула интегрирования по частям. Случаи ее применения
Данный метод интегрирования заключается во введении новой переменной интегрирования, что позволяет свести исходный интеграл к табличному.
Пусть х=φ(t) - функция, определена и дифференцируема на некотором промежутке T, и пусть X - это множество значений этой функции, на котором определена функция f(x). Тогда на множестве Х функция f(x) имеет первообразную, и на множестве Т справедлива формула:
ʃf(x)dx=ʃf(φ(t))dφ(t)=ʃf(φ(t))*φ'(t)dt
- это формула замены переменной в неопределенном интеграле.
На практике целесообразно подбирать подстановку в виде t=Ψ(x), dt=Ψ'(x)dx
и формула замены переменной примет вид:
ʃf(Ψ(x))*Ψ'(x)dx=ʃf(t)dt
Пример:
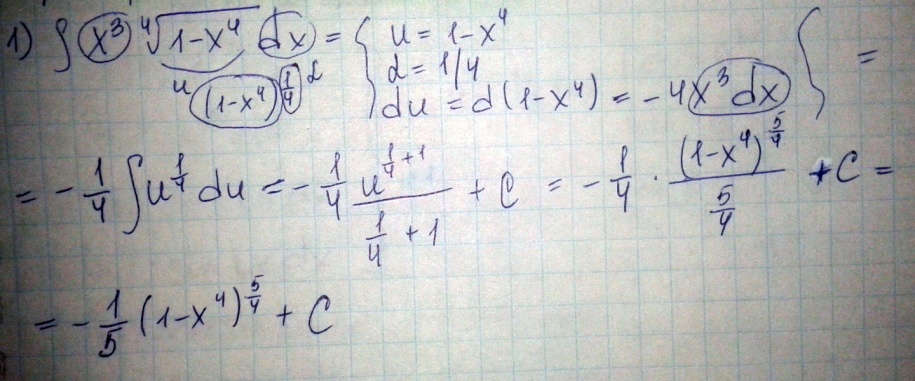
Интегрирование по частям.
Этот метод применяется в том случае, когда подынтегральная функция записана в виде произведения функций, принадлежащих разным классам интегральных функций, или является обратной тригонометрической функцией или логарифмической функцией.
Метод интегрирования по частям основывается на формуле вида:
ʃudv=uv- ʃvdu
Интегрирование по частям состоит в том, что подынтегральное выражение f(x)dx представляется в виде udv. Обязательно последний содержит dx.
Два способа:
1) при отыскании v из dv
2) при отыскании интеграла от выражения
Случаи применения формулы:
I .
ʃPn(x)*ekxdx
dv=ekxdx
.
ʃPn(x)*ekxdx
dv=ekxdx
ʃPn(x)*akxdx dv=akxdx
ʃPn(x)*coskxdx u=Pn(x) dv=coskxdx
ʃPn(x)*sinkxdx dv=sinkxdx
I I. ʃPn(x)*arcsinkxdx u=arcsinkx
ʃPn(x)*arccoskxdx u=arccoskx
ʃPn(x)*arctgkxdx u=arctgkx dv=Pn(x)dx
ʃPn(x)*arcctgkxdx u=arcctgkx
ʃPn(x)*lnkxdx u=lnkx
I II. ʃeaxsinbxdx
ʃeaxcosbxdx вычисляется двукратным интегрированием по частям.
Пример: