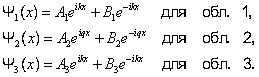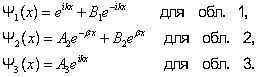- •1.Закономерности излучения черного тела. Законы Кирхгофа, Стефана-Больцмана, Вина. Формула Рэлея-Джинса. Ультрафиолетовая катастрофа.
- •2.Энергия и импульс фотона. Формула Планка для спектра излучения черного тела.
- •3.Квантовая теория фотоэффекта. Эффект Комптона.
- •4.Давление света. Опыты, подтверждающие давление света. Корпускулярно-волновой дуализм излучения.
- •6.Волновой пакет микрочастицы. Соотношение неопределенностей Гейзенберга.
- •7.Опыты Резерфорда по рассеянию -частиц. Формула Резерфорда. Модель атома Резерфорда-Бора.
- •8.Закономерности в спектрах атома водорода. Серии Лаймана, Бальмера, Пашена. Комбинационный принцип Ритца.
- •9.Дискретность квантовых состояний атома. Постулаты Бора. Опыты Франка-Герца.
- •10.Спонтанные и вынужденные переходы. Коэффициенты Эйнштейна. Спектральная плотность излучения.
- •11.Принцип работы лазера. Типы лазеров. Свойства лазерного излучения.
- •12. Волновая функция микрочастицы и ее свойства. Стационарное и нестационарное уравнение Шредингера.
- •13. Решение уравнения Шредингера для свободной микрочастицы и находящейся в потенциальной яме.
- •14. Прохождение микрочастицы через потенциальный барьер. Туннельный эффект.
- •15. Гармонический осциллятор. Квантомеханическое описание атома водорода.
- •16. Уровни энергии и схема термов щелочных металлов. Дублетная структура спектров щелочных металлов.
- •17. Магнитный и механический моменты электронов. Спин. Опыты Штерна и Герлаха.
- •18. Результирующий механический момент многоэлектронного атома. J-j и l-s связь.
- •19. Нормальный и аномальный эффекты Зеемана. Фактор Ланде.
- •20. Электронные оболочки атома и их заполнение. Принцип Паули. Правила Хунда.
- •21. Тормозное и характеристическое рентгеновское излучение. Закон Мозли.
- •22. Физические особенности в молекулярных спектрах. Энергия и спектр двухатомной молекулы. P-, q- и r-ветви.
- •23. Одномерный кристалл Кронига-Пенни. Понятие о зонной теории твердых тел. Распределения Ферми-Дирака и Бозе-Эйнштейна. Фермионы и бозоны.
- •26.Свойства и характеристика ядер. Нейтрон и протон, их свойства. Энергия связи ядра.
- •27.Свойства и модель ядерных сил. Капельная модель ядра. Формула Вейцзеккера для энергии связи. Оболочечная модель ядра.
- •28. Искусственная и естественная радиоактивность. Основной закон радиоактивного распада. Активность. Правила смещения.
- •29. Основные закономерности -распада. Туннельный эффект. Свойства -излучения.
- •35.Источники и методы регистрации элементарных частиц. Типы взаимодействий и классы элементарных частиц. Античастицы.
- •37.Физическое, химическое и биологическое воздействие ионизирующего излучения.
14. Прохождение микрочастицы через потенциальный барьер. Туннельный эффект.
Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 5.4) для одномерного (по оси х) движения частицы.
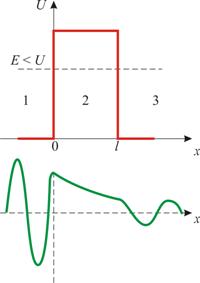
Рис. 5.4
Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать:
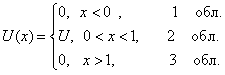
При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E>U, либо отразится от него (E<U) и будет двигаться в обратную сторону, т.е. она не может проникнуть через барьер.
Для микрочастиц же, даже при E<U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E>U имеется также отличная от нуля вероятность, что частица окажется в области x>l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи.
Уравнение Шредингера для состояний каждой из выделенных областей имеет вид:
|
|
(5.4.1) |
|
|
|
(5.4.2) |
|
Общее решение этих дифференциальных уравнений:
|
|
(5.4.3) |
|
В данном случае,
согласно (5.4.2),
![]() –
мнимое число, где
–
мнимое число, где
![]()
Можно показать, что A1 = 1, B3 = 0, тогда, учитывая значение q,получим решение уравнения Шредингера для трех областей в следующем виде:
|
|
(5.4.4) |
|
В области 2 функция (5.4.4) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые, а действительные.
Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x) показан на рис. 5.4. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой.
Таким образом, квантовая механика приводит к принципиально новому квантовому явлению –туннельному эффекту, в результате которого микрообъект может пройти через барьер.
Коэффициент
прозрачности для барьера прямоугольной
формы
![]() .
.
Для
барьера произвольной формы
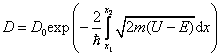 .
.
Прохождение
частицы сквозь барьер можно пояснить
соотношением неопределенностей.
Неопределенность импульса на отрезке
Δx
= l
составляет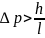 Связанная с этим разбросом кинетическая
энергия
Связанная с этим разбросом кинетическая
энергия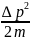 может оказаться достаточной для того,
чтобы полная энергия оказалась больше
потенциальной и частица может пройти
через барьер. С
классической точки зрения прохождение
частицы сквозь потенциальный барьер
при E<U
невозможно, так как частица, находясь
в области барьера, должна была бы
обладать отрицательной кинетической
энергией. Туннельный эффект является
специфическим
квантовым эффектом.Оказывается,
что можно обнаружить частицу за пределами
дозволенной (рис. 5.5), т.е. за точками 0 и
l(рис.
5.1).
может оказаться достаточной для того,
чтобы полная энергия оказалась больше
потенциальной и частица может пройти
через барьер. С
классической точки зрения прохождение
частицы сквозь потенциальный барьер
при E<U
невозможно, так как частица, находясь
в области барьера, должна была бы
обладать отрицательной кинетической
энергией. Туннельный эффект является
специфическим
квантовым эффектом.Оказывается,
что можно обнаружить частицу за пределами
дозволенной (рис. 5.5), т.е. за точками 0 и
l(рис.
5.1).

Рис. 5.5
Это означает, что частица может прибывать там, где ее полная энергия меньше потенциальной энергии. Это оказывается возможным вследствие туннельного эффекта.