8.Закономерности в спектрах атома водорода. Серии Лаймана, Бальмера, Пашена. Комбинационный принцип Ритца.

Для одноэлектронного атома ( с одним электроном на внешней оболочке, например, атома водорода) значения энергий атома в устойчивых состояниях могут быть определены с помощью формулы

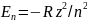
где R=2.28*10^-18 Дж - постоянная Ридберга, z - заряд атомного ядра, n - главное квантовое число, которое и характеризует полную энергию электрона в поле ядра с зарядом z_e , e- заряд электрона. Из этой формулы можно определить частоты излучения атома (частоты соответствующих спектральных линий) . Так для атома водорода.

V_nn`=R(1/n^’2-1/n²)

Если варьировать значения квантовых чисел и , то можно получить спектральные серии водорода: V_nn`=R(1/n^’2-1/n²)

n’=1, n=2,3,4,…,∞ серия Лаймана,

n’=2, n=3,4,5,…,∞ серия Бальмера.

n’=3, n=4,5,6…,∞ серия Ритца-Пашена,

Название этих серий соответствует именам ученых, экспериментально установивших эти закономерности в спектре атома водорода.

Комбинацио́нный при́нцип Ри́тца — основной закон спектроскопии, установленный эмпирически Вальтером Ритцем в 1908 году. Согласно этому принципу всё многообразие спектральных линий какого-либо элемента может быть представлено через комбинации неких величин, получивших название термы. Спектроскопическое волновое число (не путать с волновым вектором k) каждой спектральной линии можно выразить через разность двух термов:

;

Если зафиксировать   и перебирать все возможные значения  , то получится набор линий, именуемый спектральной серией. Из комбинационного принципа следует, что разность волновых чисел двух спектральных линий одной и той же серии атома даёт волновое число спектральной линии какой-то другой серии того же атома.

Следствие комбинационного принципа: Разность волновых чисел двух спектральных линий одной и той же серии атома даёт волновое число спектральной линии какой-то другой серии того же атома. Доказательство: Рассмотрим две спектральные линии одной серии:

, 

Пусть  , тогда  . Вычитая второе равенство из первого получаем

.

9.Дискретность квантовых состояний атома. Постулаты Бора. Опыты Франка-Герца.

Модель Бора выявила истинное значение спектральных законов и позволила установить, как эти законы отражают квантовый характер внутренней структуры атома — устойчивость структуры атома оказалась неразрывно связанной с существованием квантов. В модели Бора каждый атом обладает некоторой последовательностью квантовых стационарных состояний. Каждый вид атома имеет свою последовательность квантовых значений энергии, соответствующих различным возможным стационарным состояниям.Постулаты Бора:

1. В атоме существует ряд дискретных стационарных состояний.В стационарном состоянии атом не излучает и не поглощает энергии.

2 .В стационарном состоянии атом электрона двигаясь по круговой орбите должен иметь квантованое значения импульса удовлетваряющего условию

L_n=mvτ=nh,n=1,2,3,…

n=2πr/λ

3.При переходе атома из одного стационарного состояния в другое испускается или поглощается один фатон.

∆Е=hυ

Опыт Франка — Герца — опыт, явившийся экспериментальным доказательством дискретности внутренней энергии атома.

В опыте наблюдался монотонный рост I при увеличении ускоряющего потенциала вплоть до 4,9 в, то есть электроны с энергией Е 4,9 эв испытывали упругие соударения с атомами Hg и внутренняя энергия атомов не менялась. При значении V = 4,9 в и кратных ему значениях 9,8 в, 14,7 в появлялись резкие спады тока. Это определённым образом указывало на то, что при этих значениях V соударения электронов с атомами носят неупругий характер, т. е. энергия электронов достаточна для возбуждения атомов Hg. При кратных 4,9 эв значениях энергии электроны могут испытывать неупругие столкновения несколько раз. Таким образом, опыт Франка — Герца показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен, минимальная порция квант электромагнитного поля, которую может поглотить атом Hg, равна 4,9 эВ. Значение длины волны = 253,7 нм свечения паров Hg, возникавшее при V 4,9 В, оказалось в соответствии со вторым постулатом Бора.