Laboratory work.
Critical Mach number models of straight and sweep-back wings determination
The aim of work is determination after distribution of pressure for the surfaces of profile in the subsonic incompressible stream of critical Mach number of models of straight and sweep-back wings, research of influence of angle of attack and sweep-back angle on the critical Mach number.
Before to start realize of laboratory work a student must be ABLE:
To determine the geometrical parameters of profile of wing and form of wing in a plan.
To measure dynamic pressure of air flow and static pressure on the surface of model.
To determine pressure coefficient.
To measure angle of attack and sweep-back angle.
Literature: [1, chapter 12-14, 17]; [2, chapter 10, 13-15; [3, 4, 5].
Necessary theoretical information and relations/
With the increase of speed of flight of aircraft on its aerodynamic performances compressibility of stream begins to influence, that aircraft flows around. It results in a volume, that the use of not sweep-back wings becomes inadvisable both from the point of view of charges of energy that is needed for motion aircraft and from the point of view of displays of the undesirable effects related to the change of stability and controllability performances.
Therefore on large subsonic, near sonic and supersonic speeds use sweep-back wings. Thus very important characteristic of wing is a critical Mach number (Мcr). As the critical Mach number of concrete wing at set angle of attack understand the value of Mach number, that is counted up with the use of parameters of undisturbed flow that runs into a wing (V∞/а∞) in moment, when on the surface of wing even in one point a local flow velocity equals local speed of sound.
From the moment of achievement in flight of Мcr on a surface aircraft begins wave crisis. Obviously, that the increase of Мcr moves aside appearance of wave crisis on high speeds, and at flight with speeds that correspond numbers M grater than Мcr, decrease the negative consequences of wave crisis.
The quality analysis of influence of different factors(first of all geometrical) is taken to the analysis of influence of these factors on speed of flow on the surface of wing. As a wing consists of separate aerodynamic profiles, then it is expedient to examine influence of profile geometry on Мcr .On fig.1 two aerodynamic profiles are represented, that are flowed around by an identical undisturbed stream with zero angle of attack.
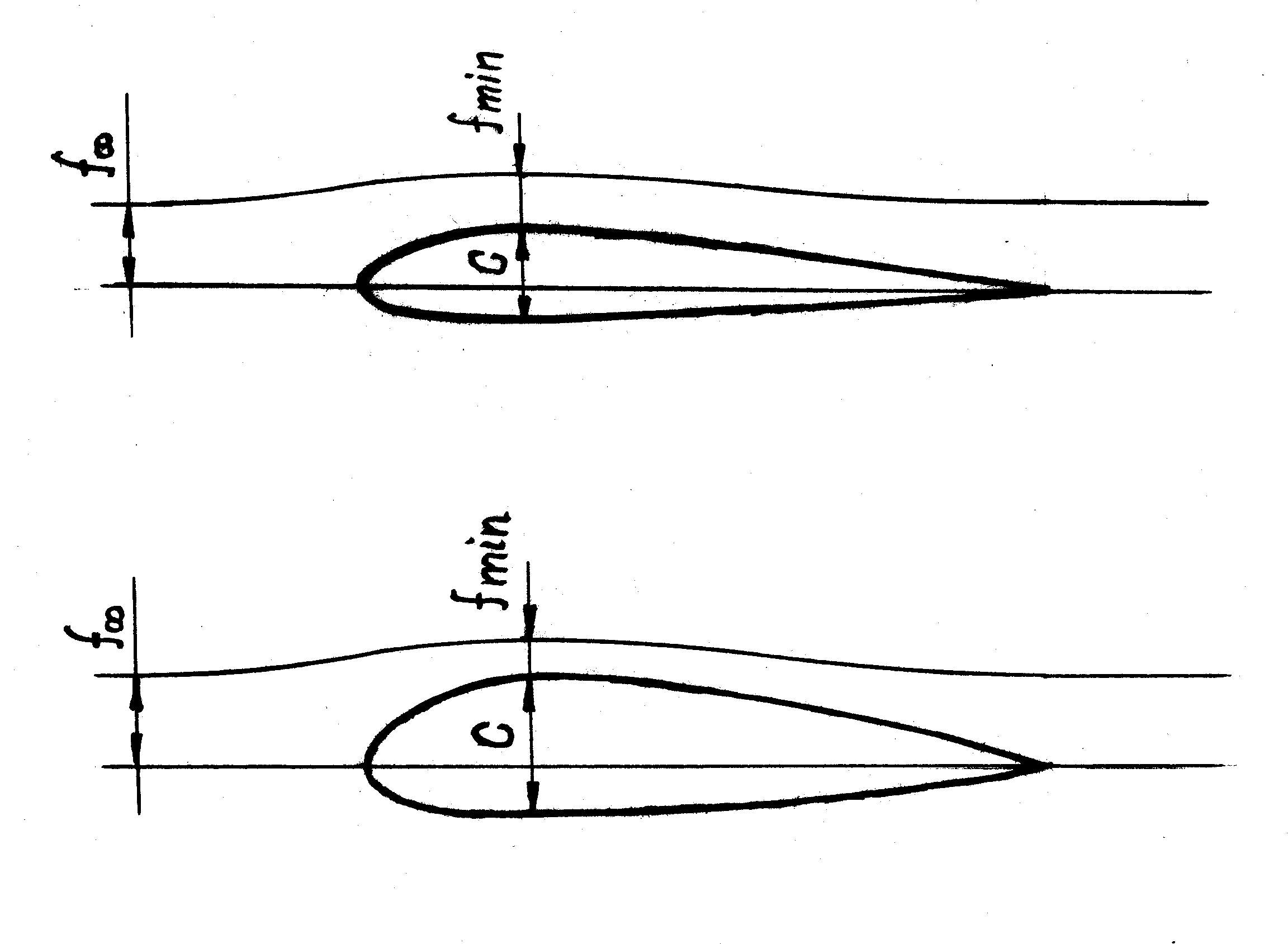
Fig. 1. Schemes of the flow around thin and thick aerodynamic profile.
One profile is thin, and second - thick. Obviously, that on the surface of profile (any) in a place that corresponds position of maximal thickness of profile, an elementary stream that moves directly along a profile will have the least area of crossing (fmin).
From mass rate equation for an elementary stream comes out, that speed in this crossing will be greatest. On the other hand, coming from Bernoulli’s equation for an elementary stream, it is possible to draw conclusion, that speed of sound in this crossing will be the least; the least also there will be static pressure. It means that a Macy number in the indicated crossing will always be most(M=V/a, V is a flow velocity in a point, a is speed of sound in a point) in comparing to any other crossing.
For the thick profile of fmin will be less than, than for thin. It, in turn, means that at the identical parameters of streams(V∞ speed, а∞ - speed of sound, р∞ - static pressure, ρ∞‑ density, Т∞ - a temperature), that run accordingly into thin and thick profiles in the least crossing of elementary stream of thin profile a Mach number will be less than corresponding Mach number is for a thick profile. At the increase of flow velocity, that appears suddenly, on a thick profile before there will be reached mode of flow when V=a, id est.critical mode : Thus for the thick profile of Мcr less than for thin.
The brought chain of reasoning is the analysis of influence of profile thickness (relative) on its critical Mach number.
On the other hand, in a point(points) on the surface of wing, where speed is maximal, static pressure and corresponding to him coefficient of pressure(taking into account a sign) are minimum. Thus, a point is on a surface, there is the most discharging in that, is the first "candidate" on the origin of the critical mode of flow at the increase of flow velocity.
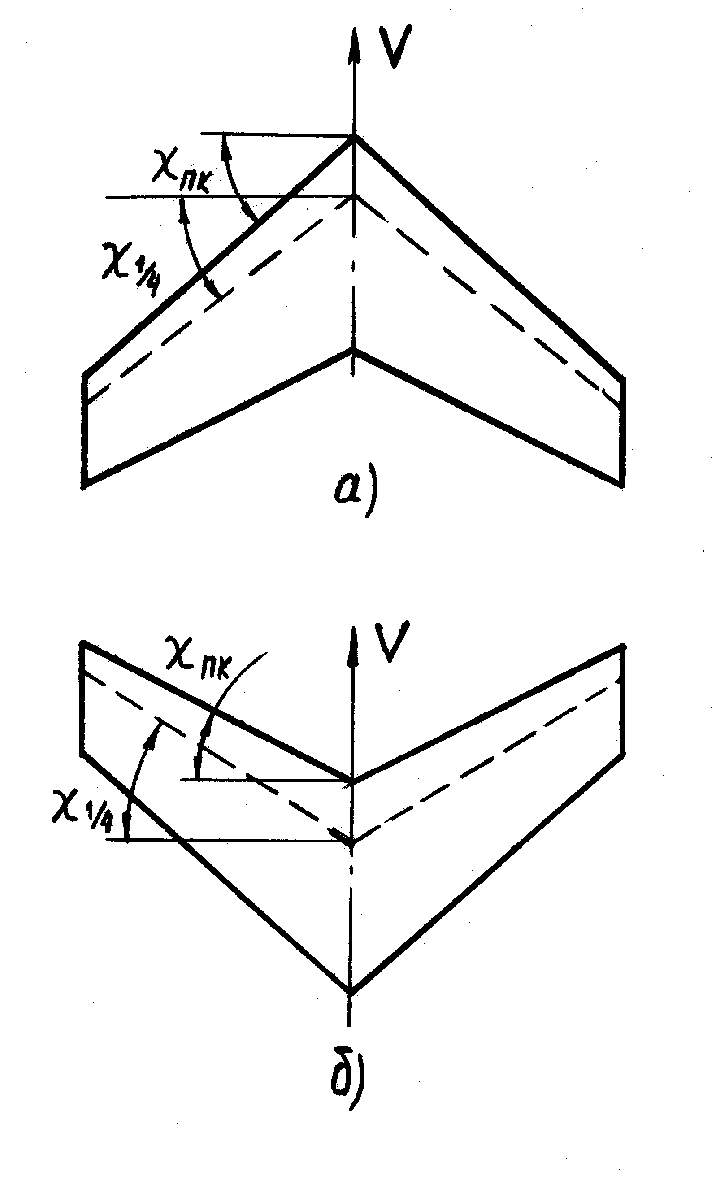
Fig.2. Sweep back wings: a is backward sweep, б- forward sweep |
Any factor that increases discharging on the surface of wing simultaneously diminishes him Мcr Such increases of angle of attack are conduced to the increase by discharging on it, and diminishes its Мcr.
Will
consider influence of parameters of form of wing in a plan on its
Мcr.
The increase of the aspect ratio of wing (
A
certain feature influence of sweepback angle
|
,
l
is a wingspan, S is an area of wing) conduces to reduction of
downwash to the stream in the separate crossing, and to the
increase of local angles of attack, and these in turn are
diminished by Мcr
(fig.2) differs in.Will consider influence of parameters of form of wing in a plan on its Мcr. The increase of the aspect ratio of wing ( , l is a wingspan, S is an area of wing) conduces to reduction of downwash to the stream in the separate crossing, and to the increase of local angles of attack, and these in turn are diminished by Мcr
Sweep
back wing name a wing, at that the line of the focuses located
approximately in the distance fourths of chord from a front edge
forms with a normal to the plane of symmetry of wing angle, that is
named the sweep back angle. Sometimes during calculations the sweep
back angle is measured not from the line of focuses, but from other
line, for example from a front or back edge. For clarification of
type of line that is used for determination of sweep back angle, near
a letter that marks the sweep back angle write a corresponding index(
and others like that (
).
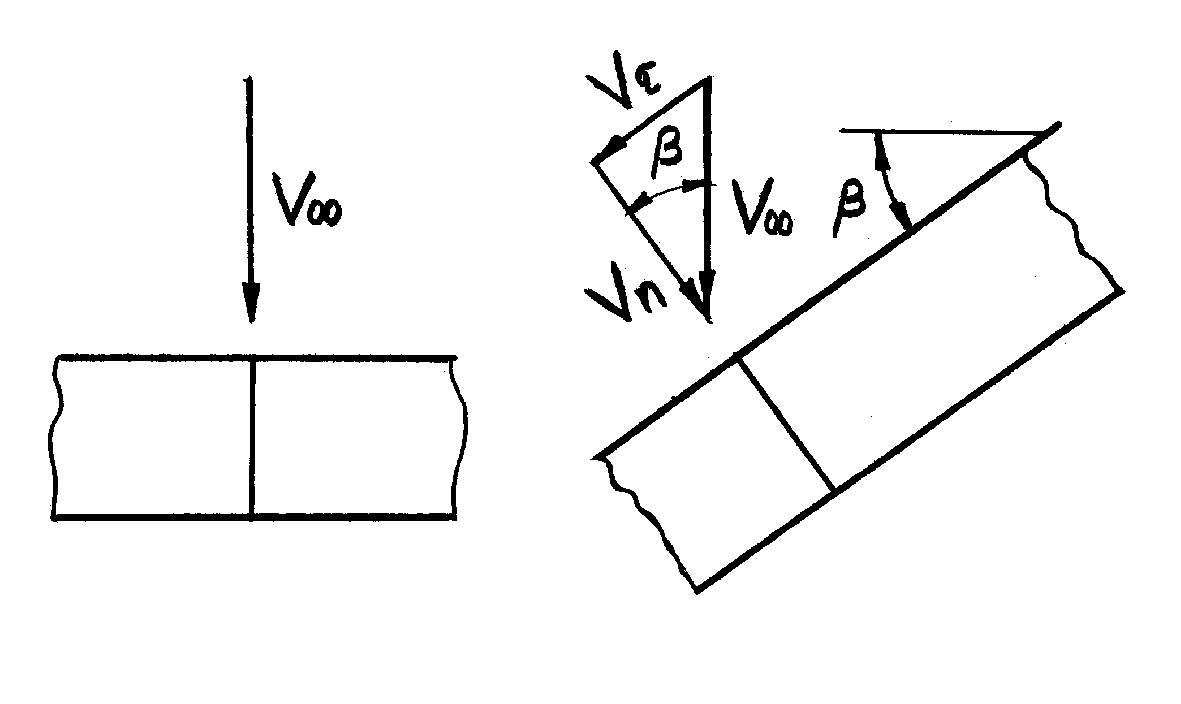
For simplification of explanation of influence of sweep back on Мcr use as an analogue of sweep back wing in case of wing of infinity span that slid (fig.3).
Fig.3. Charts of flowing around of wings: а- straight, b - sliding.
|
The
angle of sliding in this case comes forward as an analogue of
sweep back angle (
|
).
Fig. 3 explains the effect of sliding. Examine for comparison two
wings of infinite span: one straight, other sliding In both cases
the phenomenon of flowing around of profile in crossing
perpendicular to the front edge of wing are analysed.The angle of sliding in this case comes forward as an analogue of sweep back angle ( ). Fig. 3 explains the effect of sliding. Examine for comparison two wings of infinite span: one straight, other sliding In both cases the phenomenon of flowing around of profile in crossing perpendicular to the front edge of wing are analysed.
Let on a straight wing an air moves with speed V;, perpendicular to its front edge. In this case get certain distribution of pressure chordwise, that influences on aerodynamic characteristics of wing.
Let
into a sliding wing an air moves with speed V;, under the angle β
to its front edge. Speed of V;, as a vector is put out on normal to
the front edge component Vп
and
tangential - Vτ..
For a inviscid flow distribution of pressure chordwise in the
distinguished crossing is determined only by the normal component of
speed V∞,
what less than speed V∞
in cos
β
time, id est
.
If the angle of attack of profile in the distinguished crossing to
save to the same, that and for a straight wing, then a picture of
distribution of pressure is along the profile of wing, will be the
same at speed of V;, what it had to be for a direct wing at speed
equal
.
For providing of legitimacy of the got conclusions angles of attack of straight and sliding wings must be in certain correlation. Fig.4 explains the origin of these correlations.
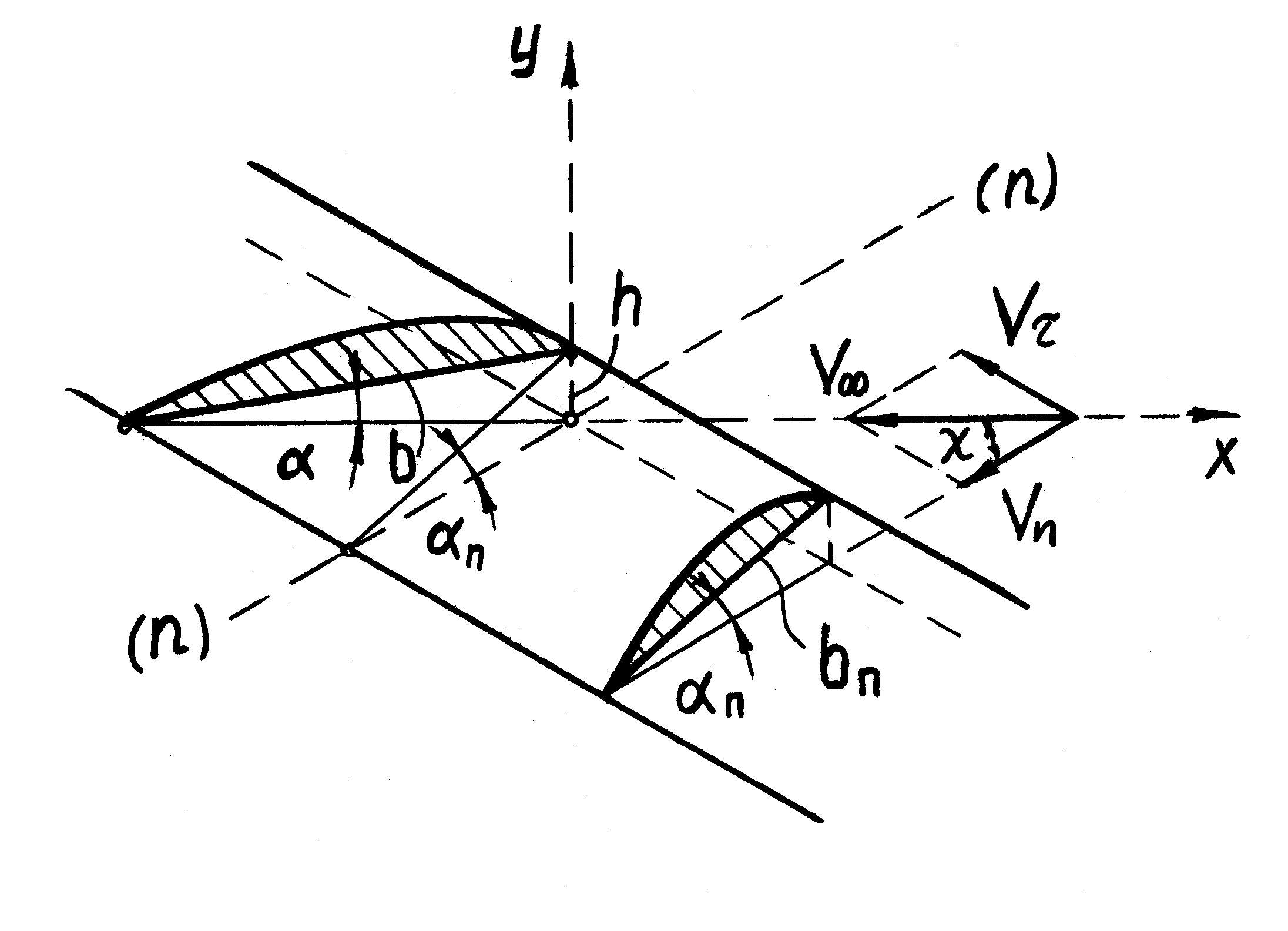
Fig.4. Chart of sliding infinite span wing.
On fig. 4 the wing of infinite span, located in relation to a stream under the sliding angle χ. According to the picture bп is a chord of wing in the normal to the front edge crossing, b is a chord of wing in crossing to the parallel stream, αп is an angle of attack of the normal crossing, α is an angle of attack in crossing to the parallel stream. In accordance to the picture it is possible to write down correlation
.
As
usually the angles of attack acquire small values, then
.
As at identical speed of flowing around straight and slide wings local speeds on the surface of sliding wing are less, then a wave crisis on a sliding wing will come at high speeds of flight. Thus in the first approaching covered the critical Mach number that sliding wing, it is possible to define from correlation
,
where Мcr slid, Мcr straight - accordingly critical Mach numbers for such that slides, and straight wings.
The picture of flowing around of sweep back wing of finite span some differs from flowing around of infinite span sliding wing, but basic physical conformities to law remain general.
Certainly, by the most reliable method of determination of value of Мcr of arbitrary wing there is realization of experiment. Value of Мcr is possible to define on results experiment with wings in a wind-channel with small subsonic speeds appear suddenly what to the stream. Between the critical number of Мcr and the minimum value of coefficient of pressure on the profile ср is unambigiuous dependence. In obedience to the hypothesis of Hristeanovich local speed of sound (at an increase of flow velocity first becomes even to the local flow velocity in the that place of profile, where in case of flowing around a inviscid stream there is the large rarefaction.
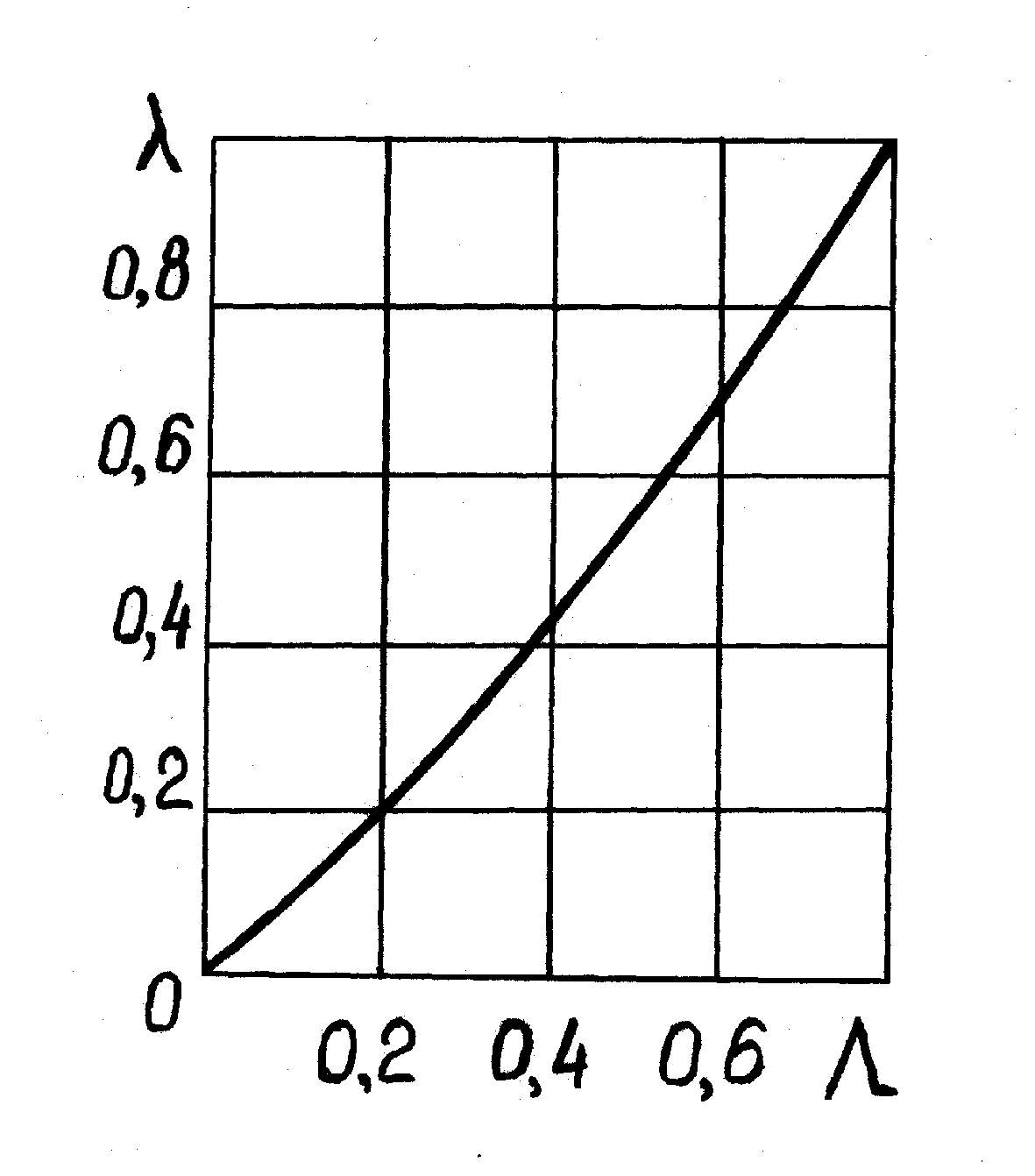
Fig.5. dependence of coefficient of speed of the compressible stream λ from the coefficient of speed of incompressible stream Λ |
Methodology of calculation of Мкр consists in the following. On results of wind tunnel tests of profile determine the value of ср min, using it find the value of local dimensionless speed Λ; of incompressible stream using a chart(fig. 5), or using approximating a formula
|
find the value of
coefficient of speed
of the compressible
stream that corresponds
value
.The critical Mach number is counted up, using the formula of connection between the coefficient of speed and Mach number.
,
where к is adiabat exponent.