8 Теорема о минимуме производства энтропии и вытекающие из нее выводы

использованы уравнения баланса массы, дифференциальное уравнение Гиббса и полученное на их основе уравнение баланса энтропии и физический смысл используемых в этих уравнениях величин ясны из рис. 2.6.

У равнение баланса массы:

(2.1)

Приведем также дифференциальное уравнение Гиббса

(2.2)

где μj – химический потенциал единицы массы компонента

Xj, Sυ – плотность энтропии, функция ρj.

Для случая равновесия это уравнение имеет следующий вид:

(2.3)

где Т – температура;

U- внутренняя энергия; р – давление; m – масса.

На основе уравнений (2.1) и (2.2) может быть получено уравнение

баланса энтропии:

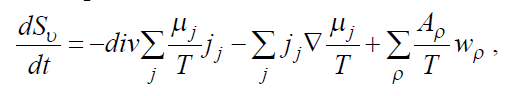(2.4)

С учетом полученных соотношений далее выводится теорема о ми-

нимальном производстве энтропии (Р). получаем следующее соотношение:

Учитывая произвольность вариаций концентраций ρi, вытекает неравенство

Тогда следует, что

dP/dt < 0 – вдали от стационарного состояния;

dP/dt = 0 – в стационарном состоянии.

Изменение производства энтропии во времени представлено на рис.2.7, что и является графической иллюстрацией теоремы о минимальном производстве энтропии, на основе которой делаются следующие утверждения.

В линейных системах выполняется общее неравенство, согласно которому в стационарном неравновесном состоянии производство энтропии имеет минимальное значение, зависящее от внешних условий, наложенных на систему.

При этом в системе могут иметь место возмущения либо внешней природы, обусловленные случайными или систематическими изменениями окружающей среды, либо внутренние флуктуации, возникающие в самой системе в результате межмолекулярного взаимодействия или случайного теплового движения частиц. В результате система непрерывно отклоняется на небольшую величину от макроскопического состояния, описываемого уравнениями баланса термодинамических переменных

9. Критерий эволюции.

A_ρ зависит от природы элементов и от отклонения термодинамического равновесия.

, где

j и W_ρ связаны с ρ_i системой нелинейных уравнений феноменологических, например, типа

Разделим производство энтропии на 2 части

В линейной области

– это следствие теоремы о минимальном производстве энтропии.

– универсальный критерий эволюции

10. Соотношение, связывающее условия термодинамической устойчивости с кинетикой химических реакций.

Соотношение δ_xP(λ_c)=0 при t≥t₀ позволяет найти внешние условия (управляющие воздействия), при которых возникает неустойчивость термодинамической ветви, и связать эти условия с кинетикой химических реакций. Определение условий, при которых может происходить потеря термодинамической устойчивости, сводится к определению знака величины δхР или в конечном итоге – знака величины

11. Упрощенный механизм образования шестигранных ячеек в модели Бенара.

Исторически первой моделью самоорганизации (формирования диссипативной структуры) являются так называемые ячейки Бенара, открытые в 1900 г. Постановка опыта очень проста: необходимо в равномерно подогреваемый снизу сосуд с плоским дном налить масло с размешанным в нем мелким порошком (рис. 3.1a).

П ока разность температур у дна и на поверхности ΔT = T₁ -T₂ невелика, жидкость неподвижна. Когда эта разность превысит определенное значение ΔTc , которое зависит от свойств жидкости и толщины слоя, вся среда разбивается на правильные шестигранные ячейки (рис. 3.1б), в центре каждой из которых жидкость поднимается вверх, а по краям – вниз. Центр тяжести элементарной ячейки жидкости как бы поднимается вверх, становится неустойчивым и опрокидывается. Дальнейшее повышение разности температур ΔТ приводит к разрушению ячеек и хаотическому (турбулентному) движению жидкости. Формирование именно шестигранных ячеек объясняется на основе принципа минимальной диссипации энергии, т.к. только в этом случае имеет место минимальное отношение поверхности к объему. Это весьма наглядный пример оптимального решения, найденного природой (неживой природой), реализуемого

посредством самоорганизации.

Рис. 3.1. Модель Бенара