
- •Классификация узлов и деталей
- •1.2 Классификация
- •Механические свойства конструкционных материалов
- •Предельные состояния и критерий расчета несущей способности
- •Требования к деталям по критериям работоспособности
- •Механические передачи и их классификация
- •Фрикционные механизмы,общие сведения,классификация
- •Фрикционные передачи с постоянным передаточным отношением
- •Кинематика фрикционного механизма
- •Материалы, критерии работоспособности и расчета фрикционных механизмов
- •3.7 Критерии работоспособности фрикционной передачи
- •3.8 Виды фрикционных передач
- •Фрикционные вариаторы
- •12.Приборные механизмы с гибкой связью. Область применения в приборостроении.
- •Приборные ременные передачи,классификация. Основные геометрические и кинематические зависимости
- •. Кинематика ременных передач
- •Геометрия ременных передач
- •Критерии работоспособности и расчета приборных ременных передач
- •Проектирование ременных передач
- •Зубчатоременные передачи
Критерии работоспособности и расчета приборных ременных передач
Критерии
работоспособности ремённых
передач
Основными
критериями работоспособности ремённых
передач являются
1) тяговая
способность – надёжность сцепления со
шкивами,
2) долговечность ремня,
которая определяется в основном его
сопротивлением усталости.
Тяговая
способность ременной передачи
обусловливается сцеплением ремня со
шкивами. Исследуя тяговую способность,
строят графики-кривые скольжения и к.
п. д.; на их базе разработан современный
метод расчета ременных передач.
Тяговая
способность характеризуется кривыми
скольжения и КПД передачи ![]() от
полезной нагрузки (окружной силы Ft),
которую выражают через коэффициент
тяги
от
полезной нагрузки (окружной силы Ft),
которую выражают через коэффициент
тяги ![]() ,
показывающий, какая часть предварительного
натяжения ремня полезно используется
для передачи нагрузки. Кривые скольжения
для всех типов ремней получают
экспериментально
При дальнейшем
увеличении коэффициента тяги от
,
показывающий, какая часть предварительного
натяжения ремня полезно используется
для передачи нагрузки. Кривые скольжения
для всех типов ремней получают
экспериментально
При дальнейшем
увеличении коэффициента тяги от ![]() до
до ![]() к
упругому скольжению добавляется
частичное буксование. Нормальная работа
передачи нарушается. Зона частичного
буксования определяет способность
передачи переносить кратковременные
перегрузки, например при пуске. При
предельном значении
наступает
полное буксование, ведомый шкив
останавливается.
В зоне частичного
буксования КПД резко снижается вследствие
увеличения потерь на скольжение, при
этом ремень быстро изнашивается. Поэтому
рабочую нагрузку рекомендуется выбирать
вблизи критического значения. В этом
случае значение КПД принимают: для
плоскоремённой передачи
=
0,93…0,98; для клино- и поликлиноремённой
=
0,92…0,97.
к
упругому скольжению добавляется
частичное буксование. Нормальная работа
передачи нарушается. Зона частичного
буксования определяет способность
передачи переносить кратковременные
перегрузки, например при пуске. При
предельном значении
наступает
полное буксование, ведомый шкив
останавливается.
В зоне частичного
буксования КПД резко снижается вследствие
увеличения потерь на скольжение, при
этом ремень быстро изнашивается. Поэтому
рабочую нагрузку рекомендуется выбирать
вблизи критического значения. В этом
случае значение КПД принимают: для
плоскоремённой передачи
=
0,93…0,98; для клино- и поликлиноремённой
=
0,92…0,97.
Проектирование ременных передач
Зубчатоременные передачи
Недостатки. 1. Сравнительно высокая стоимость. 2. Повышенная чувствительность к непараллельности валов. Распространению передачи зубчатым ремнем способствуют ее достоинства. Эластичность ремня и упругость зубьев устраняют шум и динамические нагрузки, что позволяет применять передачу в ЭВМ, киносъемочной и телевизионной аппаратуре, приводах металлорежущих станков, швейных машин и др. Мощность, передаваемая зубчатым ремнем, 100 кВт; скорость ремня υ ^ 60 м/с; к.п.д. передачи η = 0,94...0,97. Зубчатые ремни представляют собой бесконечную ленту с зубьями на внутренней поверхности (рис. 20.1). Стандартизованы. Состоят из несущего слоя — стальных тросов (диаметром 0,36 или 0,75 мм, свитых из проволоки диаметром 0,12 мм) и эластичного связывающего материала — резины или пластмассы. Для ремней приборов трос изготовляют из стекловолокна. Зубья ремня трапецеидальной формы с углом профиля 50° и 40°. Размеры ремня зависят от модуля m — основного расчетного параметра передачи. Значения m, мм: 1; 1,5; 2; 3; 4; 5; 7; 10. Шкивы зубчатоременных передач представляют собой зубчатые колеса (рис. 20.1), головки зубьев которых срезаны до диаметра
де / — расстояние от впадины зуба ремня до осевой линии троса: / = 0,6 мм при m = 2...4 мм; /=1,3 мм при т = 5...Ю мм; с — поправка, учитывающая податливость витков троса: с = = 0,08...0,18 мм при da = 50...500 мм. гШирина шкива B = b + m, где Ь — ширина ремня. Зубья на шкивах нарезают методом обкатки 16.Цепные передачи Цепная передача — это передача механической энергии при помощи гибкого элемента — цепи, за счёт сил зацепления. Может иметь как постоянное так и переменное передаточное число (напр. цепной вариатор). Состоит из ведущей и ведомой звездочки и цепи. Цепь состоит из подвижных звеньев. В замкнутое кольцо для передачи непрерывного вращательного движения концы цепи соединяются с помощью специального разборного звена. Обычно число зубьев на звёздочках и число звеньев цепи стремятся делать взаимно простыми, что обеспечивает равномерность износа: каждый зуб звёздочки будет поочерёдно работать со всеми звеньями цепи. Ц. п. универсальны, просты и экономичны. По сравнению с зубчатыми передачами они менее чувствительны к неточностям расположения валов, ударным нагрузкам, допускают практически неограниченные межцентровые расстояния, обеспечивают более простую компоновку, большую подвижность валов друг относительно друга. В сравнении с ремёнными передачами (См. Ремённая передача) они характеризуются следующими достоинствами: отсутствие проскальзывания и постоянство среднего передаточного отношения; отсутствие предварительного натяжения и связанных с ним дополнительных нагрузок на валы и подшипники; передача большой мощности как при высоких, так и при низких скоростях; сохранение удовлетворительной работоспособности при высоких и низких температурах; приспособление к любым изменениям конструкции удалением или добавлением звеньев. Достоинства:
Недостатки:
В некоторых механизмах грузоподъёмные цепи, например цепная таль с ручным приводом, выполняют роль приводных цепей. 17.Зубчатые передачи. Область применения механизмов с зубчатыми передач ами в приборных электромеханических приводах Зýбчатая переда́ча — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Назначение:
При этом усилие от одного элемента к другому передаётся с помощью зубьев. Зубчатое колесо передачи с меньшим числом зубьев называется шестернёй, второе колесо с большим числом зубьев называется колесом. Пара зубчатых колёс имеющих одинаковое число зубьев — в этом случае ведущее зубчатое колесо называется шестернёй, а ведомое — колесом. Обычно число зубьев на сопряжённых зубчатых колёсах стремятся делать взаимно простым, что обеспечивает бо́льшую равномерность износа: в этом случае каждый зуб одного колеса будет по очереди работать со всеми зубьями другого колеса. Применение зубчатых передач в приборостроении. Косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высокой скорости, либо имеющих жёсткие ограничения по шумности. Зубчатые передачи определяют качество, надежность, работоспособность и долговечность машин, станков, приборов и других изделий. Основным геометрическим параметром, определяющим все элементы передачи, является модуль m. Мелкомодульные передачи (m < 1) применяются при малых нагрузках (в приборостроении, при ручном приводе). Основные требования, предъявляемые к зубчатым передачам в приборостроении, сводятся к получению большого значения передаточного числа при малых габаритах передаточного механизма и к необходимости обеспечения наиболее точного перемещения ведомого звена. В отличие от зубчатых передач, применяемых в общем машиностроении, зубчатые передачи в приборостроении передают малые усилия, благодаря чему в большинстве случаев не требуется расчета элементов зубчатых передач на прочность. Зубчатые передачи предназначенные для изменения скорости (кинематические) применяются в точных кинематических цепях (измерительные приборы, делительные механизмы станков), имеют малый модуль и небольшую длину зуба. Зубчатые передачи предназначенные для скоростных передач входят в состав редукторов турбин, двигателей, коробок перемены передачи автомобилей, коробок скоростей станков и других быстроходных механизмов. Основное требование предъявляемое к таким передачам является плавность работы, т.е. бесшумность и отсутствие вибраций 18.Классификация зубчатых передач
19.Основной закон зацепления. Элементы зацепления, основные понятия и определения Профили зубьев механизмов передачи должны быть спроектированы строго определенным образом.. Рассмотрим связь между угловыми скоростями двух звеньев, которые образуют кинематическую пару четвертого класса.. Профиль П1 вращается с угловой скоростью ω1, а профиль П2 - с угловой скоростью ω2. Проведем через общую точку касания профилей С общую нормаль и общую касательную. Скорости точки С обозначим v1 и v2. Они направлены перпендикулярно соответственно О1С и О2С. Спроектируем эти скорости на нормаль и касательную и, кроме того, опустим перпендикуляры из центров вращения на нормаль О1М1 и О2М2. Учитывая, что вращение этих звеньев направлены в противоположные скорости, будем считать угловую скорость первого звена положительной, а второго звена – отрицательной. Тогда будем иметь
Из подобия треугольников О1М1С и Cba1 и О2М2С и Cda2 , у которых стороны взаимно перпендикулярны, имеем
Учитывая
(1) и (2), получаем
Если
Зубья шестерен и зубчатых колес должны очерчиваться такой кривой линией, которая обеспечивает необходимые условия для работы зубчатой пары. Наиболее удобными для изготовления профилями считаются следующие: эвольвентный, когда зуб очерчивается отрезком кривой эвольвенты; циклоидальный, когда головка зуба очерчивается отрезками кривой эпициклоиды, а ножка зуба - кривой гипоциклоиды, и цевочный, когда зуб очерчивается отрезком эпициклоиды Модуль может быть также выражен через отношение диаметра длительной окружности к числу зубьев m = t / π = dд, где t - шаг зацепления; dд - диаметр делительной окружности; z - число зубьев. Величины модулей стандартизированы (ОСТ 1597). Этим стандартом разрешается применять только следующие величины модулей: 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 1; 1,25; 1,5; 1,75; 2; 2,25; 2,5 (2,75); 3; (3,25); 3,5; (3,75); 4; (4,25); 4,5; 5; 5,5; 6; 6,5; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 18; 20; 22; 24; 26; 28; 30; 33; 36; 39; 42; 45 и далее через 5 мм. В скобках указаны модули, которые допускается применять в случаях особой необходимости. Головка зуба - часть зуба, находящаяся выше начальной окружности. Обычно высота головки принимается: для нормального зуба hг =m, где m - модуль в мм; для укороченного зуба hг = 0,8 m. Ножка зуба - часть зуба, расположенная ниже начальной окружности. Высота ножки принимается: для нормального зуба hн = 1,25 m, для укороченного hн = 0,8 m.
20. Основы расчета геометрии прямозубых цмлиндрических передач внешнего зацепления.
Цилиндрическая
прямозубая зубчатая передача относится
к передачам зацеплением непосредственного
контакта рис.2.3.11. Применяется при
окружных скоростях 4.4.2 Силы в зацеплении
Силы
в зацеплении определяют в полюсе
зацепления. На шестерню действует
вращательный момент, который создаёт
распределённую по контактным линиям
зуба колеса нагрузку. Эту нагрузку
заменяют равнодействующей силой
4.4.3 Расчёт на контактную прочность рабочих поверхностей зубьев Расчёт на контактную прочность рабочих поверхностей зубьев является основным критерием работоспособности зубчатых передач. Расчёт производят при контакте зубьев в полюсе зацепления П. Контакт зубьев рассматривают как контакт двух цилиндров с радиусом р1 и р2. При этом наибольшие контактные напряжения определяют по формуле Герца:
Расчет
по контактной прочности сводится к
проверке условия Определив геометрические размеры передачи, ее проверяют на контактную прочность по формуле:
где 4.4.4 Расчёт зубьев на изгиб Поломка зубьев связана с напряжениями изгиба, вследствие усталости материала отРасчет на изгиб сводится к проверке условия:
При выводе расчётной формулы для определения напряжений изгиба принимают следующие допущения: 1) вся нагрузка зацепления передаются одной парой зубьев, которая приложена к вершине зуба и направлена по нормали к его профилю (сила трения не учитываются); 2) зуб рассматривают как консольную балку прямоугольного сечения, что позволяет рассчитывать его методами сопротивления материалов. Фактически зуб представляет собой балку с изменяющейся формой. Это учитывается введением в расчётные формулы теоретического коэффициента концентрации напряжений Кт. Напряжение изгиба в опасном сечении (вблизи хорды основной окружности), т.е. напряжение на растянутой стороне зуба, где возникают усталостные трещины. Напряжения определяются отношением внешней силы к моменту сопротивления сечения. Тогда после подстановки в исходную формулу, формула проверочного расчёта прямозубых передач:
где
Модуль
зубьев m определяют расчётом на изгиб,
исходя из межосевого расстояния
Полученное
значение модуля
округляют
в большую сторону до стандартного.
Модуль колес рекомендуется принимать
минимальным. Уменьшение модуля и
соответствующее увеличение числа
зубьев способствует уменьшению
удельного скольжения, что увеличивает
надежность против заедания. При малом
модуле увеличивается коэффициент
торцевого перекрытия 21.Смещение инструмента при нарезазании зубчатых колес и влияние на работоспособность приборной зубчатой передачи
22.Степень точности и ее влияние на качество приборной зубчатой передачи. Точность передач иногда напрямую определяет точность и плавность работы всего механизма, по этому все параметры зубчатых передач четко обозначены в ГОСТ 1643-81 для цилиндрических и ГОСТ 1758-81 для конических передач. Установлены 12 степеней точностей: от 1-й до 12-й в порядке убывания точности. Необходимая степень точности определяется назначением машины и условиями работы передачи. Применение зубчатых передач в машинах в зависимости от степени точности
Для каждой степени точности установлены четыре вида норм: кинематической точности, плавности работы, контакта зубьев, бокового зазора. Кинематическая точность характеризуется наибольшей погрешностью передаточного отношения за один оборот колеса, т. е. разностью между фактическим и расчетным углами поворота ведомого колеса передачи за один оборот. Плавность работы характеризуется колебаниями угловой скорости колеса в пределах одного оборота. Обусловливается ошибками в шаге и профиле и влияет на силу ударов и шум в передаче. Нормы контакта характеризуются пятном контакта зубьев, т. е. концентрацией нагрузки на зубьях. Определяются точностью исполнения профиля зубьев и влияют на работоспособность силовых передач. Указанные нормы для каждой степени точности приведены в стандартах. Для степеней точности 1 и 2 (цилиндрическая передача) и 1, 2 и 3 (коническая передача), являющихся перспективными, допуски пока не установлены. Независимо от норм и степеней точности установлено шесть видов сопряжений зубчатых колес для цилиндрических и конических передач, характеризующихся величиной гарантированного бокового зазора между зубьями с ненагруженной стороны; А (увеличенный), В (нормальный), С (уменьшенный), D (малый), Е (весьма малый), Н (нулевой). 23.Особенность геометрии косозубых цилиндрических передач Геометрия и кинематика косозубых цилиндрических передач Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном диаметре, называют косозубыми. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение
С
увеличением угла наклона 24. Условия функционирования приборной зубчатой передачи в системе точного механизма 25.Статический нагрузки в зацеплении цилиндрических передач. 26.Динамика цилиндрических зубчатых передач 27. Виды повреждений зубчатых передач Виды повреждения передач Поломка зуба (выламывание углов или целого зуба у основания) – один из более опасных видов разрушения передач. Это связано с образованием усталостных трещин в зоне концентрации напряжений от длительной циклической нагрузки или в результате перегрузок статического и ударного действия. Поломка зубьев характерна для открытых передач и передач с высокой твердостью материалов колес. Выкрашивание – характерный вид разрушения поверхностей зубьев при хорошей смазке. Выкрашивание начинается вблизи полюсной линии (зона однопарного зацепления), где скольжение и перекатывание профилей направлены таким образом, что масло запрессовывается в усталостные микротрещины и способствует выкрашиванию частиц металла. При этом нарушаются условия образования сплошной масляной пленки и появляется металлический контакт с последующим быстрым износом или задиром поверхностей. Выкрашивание наблюдается преимущественно в закрытых передачах вследствие переменных контактных напряжений. При невысокой твердости поверхности (менее 350 НВ) выкрашивание часто носит ограниченный характер вследствие приработки зубьев. Износ зубьев – причина выхода из строя преимущественно открытых передач, недостаточно защищенных от попадания абразивных частиц: пыли, продуктов износа и др. Искажение профиля в результате износа приводит к увеличению динамических нагрузок, зазоров в зацеплении, уменьшению поперечного сечения зубьев и, следовательно, к увеличению напряжений изгиба и, как правило, к поломке зуба. Заедание наблюдается в высоконагруженных передачах и является следствием разрыва масляной пленки из-за высоких контактных давлений. Оно проявляется в образовании молекулярного сцепления частиц поверхностных слоев металла и последующего разрушения этих связей в процессе скольжения зубьев, что приводит к повреждению рабочих поверхностей. Для предупреждения заедания эффективно охлаждение смазки, применение противозадирных масел с повышенной вязкостью и химически активными добавками. Пластический сдвиг наблюдается у тяжелонагруженных тихоходных зубчатых колес, выполненных из мягкой стали. Вследствие сил трения на поверхности зубьев появляются пластические деформации с последующим сдвигом частиц материала в направлении скольжения, что приводит к образованию хребта вблизи полюсной линии у зубьев ведомого колеса и канавки у зубьев ведущего. Это нарушает правильность зацепления и приводит к разрушению зубьев. Пластический сдвиг можно устранить повышением твердости рабочих поверхностей зубьев. 28.Расчет зубчатых передач на прочность по контакным напряжениям Расчёт на контактную прочность рабочих поверхностей зубьев Расчёт на контактную прочность рабочих поверхностей зубьев является основным критерием работоспособности зубчатых передач. Расчёт производят при контакте зубьев в полюсе зацепления П. Контакт зубьев рассматривают как контакт двух цилиндров с радиусом р1 и р2. При этом наибольшие контактные напряжения определяют по формуле Герца: (2.3.16) Расчет по контактной прочности сводится к проверке условия . После преобразования формулы Герца для контакта цилиндрических поверхностей получают формулу для определения межосевого расстояни
Определив геометрические размеры передачи, ее проверяют на контактную прочность по формуле: (2.3.18) 29.Расчет цилиндрических передач на выносливость при изгибе Расчёт зубьев на изгиб Поломка зубьев связана с напряжениями изгиба, вследствие усталости материала от длительно действующих нагрузок. Расчет на изгиб сводится к проверке условия: (2.3.19) При выводе расчётной формулы для определения напряжений изгиба принимают следующие допущения: 1) вся нагрузка зацепления передаются одной парой зубьев, которая приложена к вершине зуба и направлена по нормали к его профилю (сила трения не учитываются); 2) зуб рассматривают как консольную балку прямоугольного сечения, что позволяет рассчитывать его методами сопротивления материалов. Фактически зуб представляет собой балку с изменяющейся формой. Это учитывается введением в расчётные формулы теоретического коэффициента концентрации напряжений Кт. Распределённую по ширине венца зуба нагрузку заменяют сосредоточенной силой , которую переносят по линии действия на ось зуба и раскладывают на две составляющие: изгибающую зуб и сжимающую . Напряжение изгиба в опасном сечении (вблизи хорды основной окружности), т.е. напряжение на растянутой стороне зуба, где возникают усталостные трещины Напряжения определяются отношением внешней силы к моменту сопротивления сечения. Тогда после подстановки в исходную формулу, формула проверочного расчёта прямозубых передач: Зубья шестерни и колеса будут иметь примерно равную прочность на изгиб при условии (2.3.21) Модуль зубьев m определяют расчётом на изгиб, исходя из межосевого расстояния , полученного из условия контактной прочности . Полученное значение модуля округляют в большую сторону до стандартного. Модуль колес рекомендуется принимать минимальным. Уменьшение модуля и соответствующее увеличение числа зубьев способствует уменьшению удельного скольжения, что увеличивает надежность против заедания. При малом модуле увеличивается коэффициент торцевого перекрытия . То есть увеличивается плавность работы зацепления и к.п.д., уменьшается шум.
30. Проектный расчет зубчатой передачи. Проверочный расчет по критерию прочности Для проведения проектного расчета необходимы следующие исходные данные: 1. Вид передачи (прямозубая, косозубая, шевронная и др.); 2. Циклограмма вращающих моментов или наименование типового режима нагружения с указанием величины пикового кратковременно действующего вращающего момента на шестерне;
3. Вращающий
момент на шестерне (т.е.
наибольший из действующих моментов
при нормально протекающем процессе
эксплуатации-
4. Требуемый
ресурс передачи -
5. Частота
вращения шестерни -
6. Передаточное
число - 7. Марка стали шестерни и колеса; 8. Вид термообработки шестерни и колеса; 9. Твердость поверхности и сердцевины зубьев шестерни и колеса
10.Предел
текучести материала шестерни и
колеса - 11.Условия смазывания (закрытая или открытая передача); 12.Схема механизма (редуктора), уточняющая расположение рассчитываемой передачи относительно опор.
31.Материалы для изготовления приборных зубчатых колес. Расчет допускаемых напряжений. Основные металлические материалы для зубчатых, червячных колес и червяков. Конструкционные стали 20; 25; 30; 40; 45; 50 . Область применения: Для колес, червяков и трибок. Стали 20 и 25 требуют цементации, трибы и червяки из сталей 30, 40, 45, 50 желательно калить. Детали требуют антикоррозионного покрытия. Инструментальные стали У10А; У12А. Область применения: Для сильно нагруженных червяков и трибок. Хорошо калятся. Детали требуют антикоррозионных покрытий. Нержавеющие стали 2Х13; 3Х13; 4Х13; Х18Н10Т Область применения: Для колес, червяков и трибок. Требуют подкалки в заготовке до HRC 28…32. Не требуют антикоррозионных покрытий. Сталь Х18Н10Т – для деталей механизмов в маломагнитном исполнении. Латуни ЛС59-1; ЛМц 58-2; ЛЖМц59-1-1 Область применения: Для колес цилиндрических, конических, винтовых и червячных при средних условиях эксплуатации. С антикоррозийными покрытиями и без них. Бронзы Бр.АЖМц10-3-1,5; Бр.АМц9-2, Бр.Б2 Область применения: Для колес цилиндрических, конических, винтовых и червячных при тяжелых условиях эксплуатации. Без антикоррозийных покрытий. Сплавы Д16; АМг6; В95 Область применения: Для малонагруженных колес при ограниченном весе механизма. Основные металлические материалы для зубчатых и червячных колес. Фторопласт – для зубчатых колес волновых передач, упруго деформирующихся при работе. Текстолит ПТК – для зубчатых и червячных колес при требовании бесшумности передачи. Модуль не менее 0,5 мм. Работают в паре с металлическими колесами и червяками. Зубонарезание обычными методами. Полиэтилен НД, полипропилен, полиамидная смола марок А и Б, полиформальдегид – для зубатых и червячных колес. Метод изготовления – прессование и литье под давлением. Зубья требуют проверки на прочность при изгибе. При расчете то допускаемым напряжениям конструкция рассматривается в ее рабочем состоянии под действием нагрузок, допускаемых при нормальной эксплуатации сооружения, т. е. нормативных нагрузок. Условие прочности конструкции заключается в том, чтобы напряжения в конструкции от нормативных нагрузок не превышали установленных нормами допускаемых напряжений, которые представляют собой некоторую часть от предельного напряжения материала, принимаемого для строительной стали равным пределу текучести σт. Таким образом, основные формулы проверки прочности конструкции имеют вид
где σ — напряжения в конструкции от нормативных нагрузок; [σ] — допускаемые напряжения, которые установлены соответствующими нормативнымидокументами; σт —пределтекучестистали; k0 —коэффициентзапасапрочности. Коэффициент запаса введен здесь потому, что возможны отклонения как фактической нагрузки от той теоретической, которая принята в расчете, так и действительной конструкции сооружения от той теоретической схемы, которая рассчитывается. Эти возможные отклонения перекрываются коэффициентом запаса (в среднем равным примерно 1,5), который, таким образом, связывает расчетные предположения с фактической работой конструкции в процессе ее эксплуатации. 32.Приборные зубчатые механизмы с пересекающимися осями,особенности геометрии. Точность конической передачи.
Конические
зубчатые колёса применяют в передачах,
оси валов которых пересекаются под
некоторым межосевым углом
Применяют
во всех отраслях машиностроения, где
по условиям компоновки машины необходимо
передать движение между пересекающимися
осями валов. Конические передачи
сложнее цилиндрических, требуют
периодической регулировки. Для
нарезания зубчатых конических колес
необходим специальный инструмент. В
сравнении с цилиндрическими конические
передачи имеют большую массу и габарит,
сложнее в монтаже. Кроме того, одно из
конических колёс, как правило шестерня,
располагается консольно. При этом,
вследствие повышенной деформации
консольного вала, увеличиваются
неравномерность распределения нагрузки
по ширине зубчатого венца и
шум.
Конические колёса бывают
с прямыми и круговыми зубьями.
Передаточное
числа при межосевом угле 4.6.2 Геометрические параметры конического зубчатого колеса Основные геометрические размеры определяют в зависимости от модуля и числа зубьев. Высота и толщина зубьев конических колёс постепенно уменьшается по мере приближения к вершине конуса. Соответственно изменяются шаг, модуль и делительные диаметры, которых может быть бесчисленное множество. Основные геометрические размеры имеют обозначения, принятые для прямозубых конических передач
Внешний
диаметр
где
Средние делительные диаметры:
В
соответствии с исходным контуром
прямозубых конических колёс радиальный
зазор c=0,2
,
тогда
внешняя
высота головки зуба
Угол
ножки зуба
33.Основы
расчета на прочность по напряжениям
изгиба и контактным напряжениям
Расчет
конических зубчатых колес, по контактным
и изгибным напряжениям.
Для
прямозубой передачи профили зубьев
конического колеса, построенные на
развертке дополнительного конуса,
весьма близки к профилям зубьев
эквивалентного цилиндрического
прямозубого колеса, делительная
окружность которого получена разверткой
дополнительного конуса на
плоскость.
Дополнив
развертку до полной окружности получим
эквивалентное цилиндрическое с числом
зубьев 34.Проектные расчеты конической передачи 35.Приборные планетарные и дифференциальные зубчатые механизмы. Передача, имеющая в своем составе зубчатые колеса с движущимися геометрическими осями, называется планетарной. Такое название она получила потому, что одновременное вращение колеса вокруг своей оси и оси неподвижного колеса подобно движению планет вокруг Солнца. Планетарные передачи весьма компактны и позволяют получать очень большие передаточные отношения. Их применяют в приводах некоторых станков, авиационных двигателях, счетных устройствах. Ведущим колесом планетарной передачи является зубчатое колесо 1, которое называется центральным, или солнечным. В зацеплении с ним находится колесо 2, называемое сателлитом (спутником) и связанное с солнечным колесом водилом 3. Чтобы иметь возможность вращаться вокруг солнечного колеса и тем самым приводить в движениеводило, сателлит внутренним зацеплением соединен с зубчатым колесом 4, которое неподвижно закреплено в корпусе механизма и называется неподвижным,или упорным, колесом. Если в рассмотренной передаче освободить упорное колесо, то получится дифференциальная передача. В этом случае движение водила (оно является ведомым) будет результатом сложения двух независимых движений ведущих колес 1 и 4. Дифференциальные механизмы позволяют не только суммировать два движения, но и наоборот, передаватьдвижение от одного ведущего вала к двум валам при разной их относительной скорости 36.Кинематика планетарного механизма 37.Особенности расчетов на прочность планетарных механизмов. 2. Передаточное число планетарных передач При определении передаточного числа планетарной передачи используют метод остановки водила (метод Виллиса). По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с угловой скоростью водила, но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами. 3. Разновидности планетарных передач Существует большое количество различных типов планетарных передач. Выбор типа передачи определяется ее назначением. Наиболее широко в машиностроении применяется однорядная планетарная передача, схема которой показана на рис. 1. Это передача имеет минимальные габариты. Применяется в силовых и вспомогательных приводах. К.п.д. передачи л =0,96...0,98 при и = 3,15...12,5. Для получения больших передаточных чисел в силовых приводах применяют многоступенчатые планетарные передачи. 4. Подбор чисел зубьев планетарных передач На практике наибольшее распространение получила планетарная однорядная прямозубая передача (см. рис. 1), расчет которой и рассматривается ниже. Числом зубьев центральной шестерни 1 задаются из условия неподрезания ножки зуба, принимая для нее z1>17. Число зубьев неподвижного центрального колеса 3 определяют по заданному передаточному числу из формулы (2): z3=z1(и-1). (4) 5. Расчет на прочность планетарных передач Расчет на прочность зубьев планетарных передач ведут по формулам обыкновенных зубчатых передач. Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на рис. 12.1, необходимо рассчитать внешнее зацепление колес 1 и 2 и внутреннее -- колес 2 и 3. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочней внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление. При определении допускаемых напряжений коэффициенты долговечности Кhl и Kfl находят по числу циклов N' перемены напряжений зубьев за весь срок службы при вращении колес только относительно друг друга. Радиальную силу определяют, как в обычных передачах. 38. Приборные зубчатые механизмы с реечными передачами. Область применения,достоинства и недостатки. Реечная передача (кремальера) (фр. crémaillère) — один из видов механических передач, преобразующий поступательное движение во вращательное. Состоит из ведущей шестерёнки и зубчатой рейки, по которым она перемещается. Может использоваться, например, в качестве механизма для передвижения объективной доски камеры или других приспособлений (теодолита, нивелира…) при наводке объектива на резкость. Реечная передача использовалась в старых складных фотокамерах, рассчитанных на фотоматериалы большого формата (плёнки и фотопластинки); в телескопах реечная передача широко применяется для фокусировки изображения — так называемый реечный фокусер. Кремальерой также может называться ручка регулировки прибора, например ручка настройки высоты в авиационном высотомере либо замок корабельного люка, действующий по тому же принципу[1]. В медицинской технике кремальера — конструктивный элемент инструмента, служащий для фиксации его рабочих органов в заданном положении с помощью зубчатой насечки. 39.Основы расчета реечных передач Кинематический и геометрический расчет передачи Реечную передачу можно рассматривать как частный случай зубчатой передачи, одно из колес которой обращено в рейку. Скорость поступательного движения рейки:
где m - окружной делительный модуль реечной шестерни, мм; n1 - частота вращения реечной шестерни; z1 - число зубьев реечной шестерни. В соответствии с ГОСТ 10242-81 контур рейки определяется исходным контуром. Модуль, как правило, предварительно определяется исходя из кинематических требований, а затем производится проверка зубьев шестерни на изгиб. Диаметр делительной окружности шестерни:
здесь
n1,
об/мин; vср ,
м/с, тогда модуль
40.Многоступенчате приборные зубчатые механизмы. Разбивка передаточного числа механизмов по критериям минимизации массы,габаритов,приведенного момента инерции ипогрешности 41.Расчет точности многоступенчатого механизма 42.Приборные механизмы с червячными передачами. Области применения червячных передач Червя́чная переда́ча (зубчато-винтовая передача) — механическая передача, осуществляющаяся зацеплением червяка и сопряжённого с ним червячного колеса[1]. Червяк представляет собой винт со специальной резьбой, в случае эвольвентного профиля колеса форма профиля резьбы близка ктрапецеидальной[2]. На практике[2] применяются однозаходные, двухзаходные и четырёхзаходные червяки. Червячное колесо представляет собой зубчатое колесо. В технологических целях червячное колесо, как правило[2], изготовляют составленным из двух материалов: венец — из дорогого антифрикционного материала (например из бронзы), а сердечник — из более дешёвых и прочных сталейили чугунов. Входной и выходной валы передачи скрещиваются, обычно (но не всегда) под прямым углом. Передача предназначена для существенного увеличения крутящего момента и, соответственно, уменьшения угловой скорости. Ведущим звеном является червяк. Червячная передача без смазки и вибрации обладает эффектом самоторможения и является необратимой: если приложить момент к ведомому звену (червячному колесу), из-за сил трения передача работать не будет. Червячная передача главным образом применяется в червячных редукторах. Достаточно часто червячные передачи используются в системах регулировки и управления — самоторможение обеспечивает фиксацию положения, а большое передаточное отношение позволяет достичь высокой точности регулирования (управления) и(или) использовать низкомоментные двигатели. Благодаря этим же характеристикам червячные передачи и червячные редукторы широко применяются в подъёмно-транспортных машинах и механизмах (например, лебёдках) Часто в виде червячной пары изготавливаются механизмы натяжения струн (колковая механика) музыкальных инструментов, например гитары.[4] В данном применении полезным оказывается эффект самоторможения (необратимость)
|

 ;
(1)
;
(1) .
(2)
.
(2)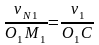 и
и
 .
. ,
а
,
а
 .
. ,
то профиль П1
либо должен проникнуть в профиль П2,
либо отстать от него, что исключается.
Поэтому должно быть
,
то профиль П1
либо должен проникнуть в профиль П2,
либо отстать от него, что исключается.
Поэтому должно быть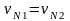 и
и
 ,
откуда
,
откуда
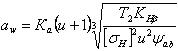

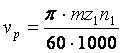 м/с,
м/с, мм,
мм,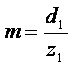 мм.
Расчетное значение модуля согласуется
с ГОСТ 9563-60. Для косозубой передачи
определяется нормальный модуль
мм.
Расчетное значение модуля согласуется
с ГОСТ 9563-60. Для косозубой передачи
определяется нормальный модуль  ,
значение которого согласуется с тем
же стандартом. Угол наклона зуба β
рекомендуется принимать не более 20°.
,
значение которого согласуется с тем
же стандартом. Угол наклона зуба β
рекомендуется принимать не более 20°.