8.6.1 Схема двоїстого симплекс–методу

8.6.1.1 Злп на максимум

Крок 0. Отримати початковий оптимальний не допустимий базисний розв’язок

Крок 1. Вибір змінної що виводиться з множини базисних (умова допустимості)

З базису виводиться змінна, у якої (зазвичай обирається найбільша по модулю від’ємна змінна, тобто ведучий рядок обирається так: ).

Якщо всі базисні змінні  0, (тобто такого не існує) то СТОП, отримали допустимий і оптимальний розв’язок.

Інакше змінна має бути виведена з базису.

Крок 2. Вибір змінної що вводиться в множину базисних (умова оптимальності)

Визначимо коефіцієнт за формулою:

і нехай мінімум досягається при . Отже, змінна вводиться в множину базисних.

Ознака відсутності допустимих розв’язків

Якщо в рядку, відповідному змінній, що виводиться, немає жодного для , відповідних небазисним змінним, тобто не існує невід’ємного яке зробило б допустимим то СТОП, пряма задача не має допустимих розв’язків.

Інакше перейти на крок 3.

Крок 3. Перехід до нового ДБР

За допомогою елементарних перетворень Гауса виконати операцію заміщення. Перехід на КРОК1.

8.6.1.2 ЗЛП на мінімум

Схема двоїстого симплекс–методу для задачі мінімізації ЦФ відрізняється від схеми для задачі на максимум правилом вибору змінної, що вводиться до множини базисних (в цьому випадку погіршення значення ЦФ – це його збільшення).

Коефіцієнт визначається за формулою:

,

(9)

(оскільки  0, то чисельник завжди  0, як і раніше розглядаються тільки відношення з від’ємним знаменником).

З урахуванням (8) і (9) можна узагальнити правило вибору змінної, що вводиться до множини базисних:

.

Ознака відсутності допустимих розв’язків для задачі мінімізації ЦФ така сама: у рядку, відповідному змінній, що виводиться, немає жодного для , відповідних небазисним змінним.

8.6.2 Особливості двоїстого симплекс–методу

За відсутності виродженості при застосуванні прямого симплекс–метода рухаємося у напряму нормалі від ДБР до ДБР, покращуючи значення ЦФ. В двоїстому ж симплекс–методі рухаємося в напрямі, зворотному напряму нормалі, від недопустимого БР (розв’язку кращого, ніж всі допустимі – для нього виконується умова оптимальності і ми кажемо,що він - оптимальний) до недопустимого БР (але, як і раніше «оптимальному»), погіршуючи значення ЦФ. Розв’язок, в який переходимо в результаті ітерації двоїстого симплекс–метода є «більш допустимим», тобто він знаходиться ближче до множини допустимих розв’язків. В результаті ми потрапимо в МДР і, отже, зупинимося.

Розглянемо можливі шляхи розв’язання задачі на мінімум (рисунок 4) двоїстим симплекс–методом, якщо стартовою є точка .

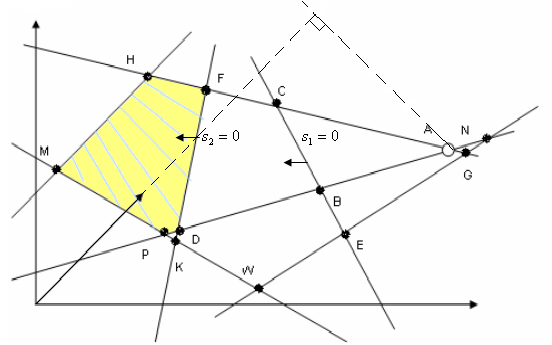
Рисунок 4

1) Якщо , то на першій ітерації виводимо з базису змінну , тобто на наступній ітерації ми обов'язково перейдемо на пряму (на якій =0 !). З точки на пряму можна перейти по двом ребрам: і . При цьому, згідно теорії двоїстого симплекс–метода ми повинні мінімально погіршити значення ЦФ, тобто – попасти в ту точку (базисний розв’язок) прямої , яка знаходиться до т. найближче. Це означає, що, рухаючи перпендикуляр до нормалі цільової функції від точки у напрямі множини допустимих розв’язків, нам спочатку зустрінеться точка (це найближчий базисний розв’язок на прямій , в який можна перейти з т. ). Міркуючи аналогічно, робимо висновок, що на наступній ітерації ми повинні перейти на пряму , на якій , тобто в точку (допустимий і оптимальний розв’язок). Отже оптимальна точка у цьому випадку досягається шляхом: .

2) Якщо , то на першій ітерації виводимо з базису змінну . Це означає, що рухаючи перпендикуляр до нормалі цільової функції від точки у напрямі множини допустимих розв’язків, переходимо на пряму , на якій , тобто в точку (оскільки вона є найближчим базисним розв’язком з точок і ). Отже оптимальна точка у цьому випадку досягається шляхом: .

Розглянемо тепер задачу на максимум (рисунок 5). Нехай початковою є точка . В цій точці недопустиме значення приймає змінна . Отже, вона виводиться з базису і на наступній ітерації ми попадемо на пряму , на якій . На цю пряму з точки можна прийти по одному з двох ребер: або . Ближчою є точка (вона ще не допустима, у неї ). І уже з цієї точки на другій ітерації ми попадемо в оптимальну точку .

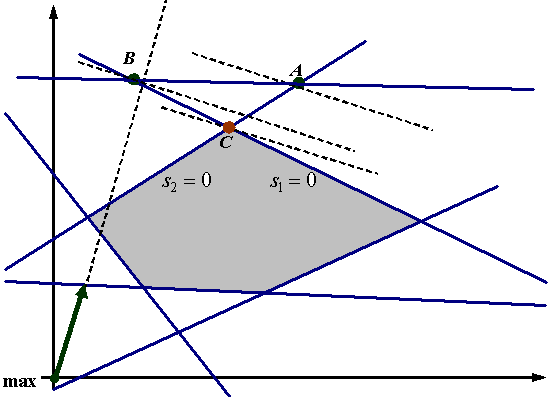
Рисунок 5