8.6 Двоїстий симплекс-метод
На кроці 1 симплекс-метода
в процесі обчислення компонентів вектора
обчислюється вектор
,
який називається вектором оцінок
обмежень. У точці оптимуму маємо
.
На кожній ітерації симплекс - метода
значення ЦФ визначається так:
.
Таким чином, на будь-якій
ітерації вектор оцінок
виступає як міра зміни ЦФ щодо вектора
обмежень
.
Якщо ми визначимо двоїсті змінні
з рівняння
для кожної ітерації симплекс - метода,
то для поточних розв’язків задач (ПЗ і
ДЗ) основна нерівність теорії двоїстості
буде завжди виконуватись як рівність,
але двоїсті змінні
будуть недопустимими впродовж усіх
ітерацій симплекс - метода до тих пір,
поки не буде досягнутий оптимальний
розв’язок.
Нехай задана ЗЛП в канонічній формі (пряма задача).
|
(1) |
|
(2) |
|
(3) |
,
,
.Якщо вектор двоїстих
змінних позначити через
,
то задача, двоїста до задачі (1)-(3), має
вигляд :
Критерій оптимальності задачі (1)-(3) такий:
,
де
- вектор відносних оцінок небазисних
змінних,
- вектор оцінок обмежень.
Як і раніше по аналогії
з вектором
введемо вектор
:
.
Тоді вектор відносних
оцінок змінних:
визначається так:
.
З урахуванням цього критерій (умову) оптимальності задачі (1)-(3) можна записати так:
,
|
(4) |
.Умова оптимальності
(4) розв’язку ПЗ є ні що інше, як умова
допустимості вектора двоїстих змінних
:
.
Таким чином, можна вважати, що в симплекс - методі ми, підтримуючи допустимість прямого розв’язку, прагнемо до допустимості двоїстого. Такий алгоритм називається прямим. Так само можна почати з допустимого двоїстого розв’язку і прагнути до допустимості прямого. Такий алгоритм називатимемо двоїстим симплекс - методом.
Нехай
– деякий базисний розв’язок задачі
(1) -(3), тоді відповідна пряма перетворена
задача має вигляд:
|
(5) |
|
(6) |
Припустимо, що двоїстий розв’язок цієї задачі допустимий, тобто виконуються умови оптимальності базисного розв’язку прямої задачі, але розв’язок прямої задачі не обов'язково є допустимим.
Тобто передбачається,
що для БР
виконується умова оптимальності
,
але не виконується умова допустимості, тобто
.
Це означає, що маємо “оптимальний” але недопустимий розв’язок прямої задачі і при цьому поточний базис визначає допустимий, але неоптимальний розв’язок двоїстої задачі.
Ідею метода проілюструємо на наступному прикладі.
Приклад
Розглянемо ЗЛП (ПЗ).
,
,
,
.
Приведемо її до стандартної форми. Це нам потрібно для того, щоб потім використати деякі особливості симетричної пари двоїстих задач.
ПЗ в стандартній формі
,
,
,
.
ПЗ в канонічній формі
,
,
,
.
А тепер побудуємо ДЗ:
,
,
,
.
Приведемо задачу до стандартної форми
,
,
,
.
ДЗ в канонічній формі:
,
,
,
.
В цьому випадку розв’язувати ДЗ простіше, ніж ПЗ.
Розглянемо такий
базисний розв’язок ДЗ:
:
–
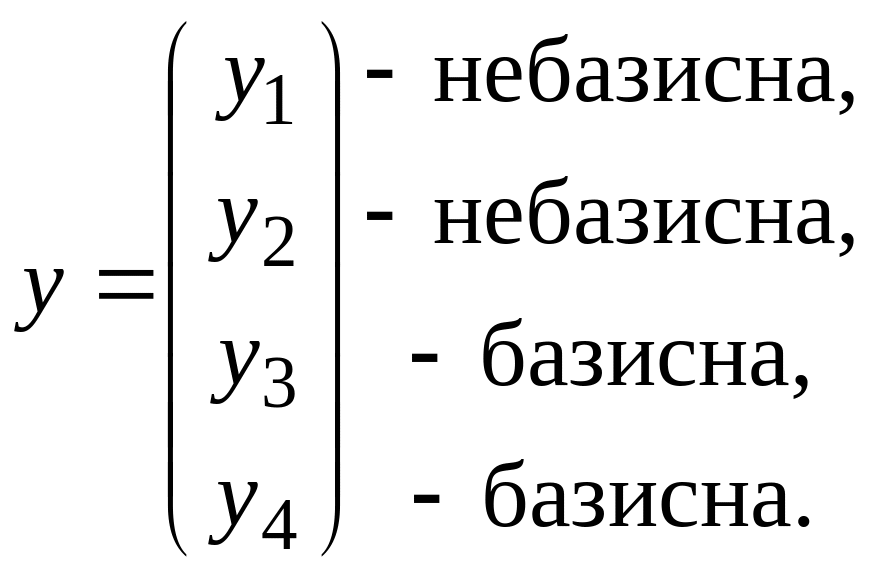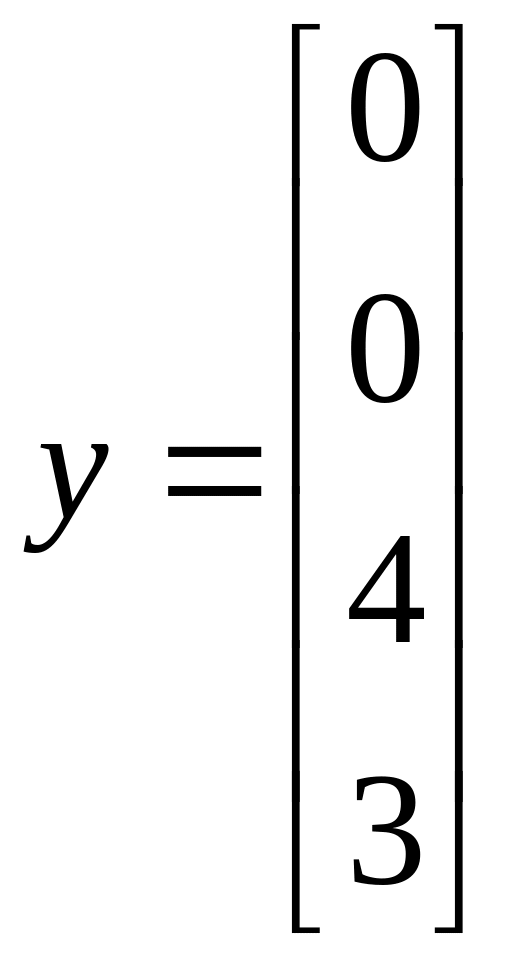допустимий розв’язок ДЗ, але не
оптимальний, оскільки для нього маємо:
.
Заповнимо початкову симплекс–таблицю для ДЗ:
БЗ |
|
|
|
|
Розв’язок |
|
2 |
-5 |
0 |
0 |
0 |
|
1 |
-2 |
1 |
0 |
4 |
|
2 |
-3 |
0 |
1 |
3 |
Подальший процес
розв’язання цієї задачі нам відомий
(
вводимо в базис,
виводимо і так далі).
А тепер розглянемо
базисний розв’язок ПЗ:
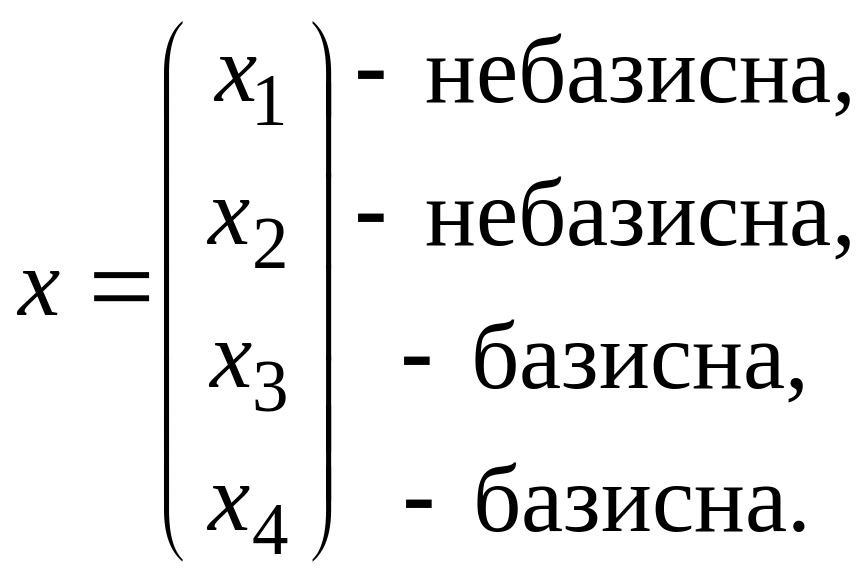
Обчислимо відповідний вектор відносних оцінок:
=
–
=
для розв’язку
виконується умова оптимальності. Але
при цьому:
цей розв’язок недопустимий.
Заповнимо початкову симплекс–таблицю:
БЗ |
|
|
|
|
Розв’язок |
|
4 |
3 |
0 |
0 |
0 |
|
-1 |
-2 |
1 |
0 |
-2 |
|
2 |
3 |
0 |
1 |
5 |
Як бачимо, вона має «незвичний» вигляд.
Ми знаємо, як розв’язувати ДЗ, що і станемо робити. Однак при цьому не будемо в явному виді виписувати ДЗ (її вигляд будемо «мати на увазі») і за симплекс-таблицею ПЗ (на максимум) будемо розв’язувати ДЗ (задачу на мінімум). В цьому і є ідея двоїстого симплекс–метода.
Визначимо умови оптимальності і допустимості двоїстого симплекс–метода і порядок їх перевірки.
Початковий розв’язок двоїстого симплекс–метода, застосованого до ПЗ, такий:
він задовольняє умовам оптимальності (будемо казати, що він оптимальний);
він не допустимий.
Наша мета:
досягти допустимості розв’язку ПЗ, не порушуючи його оптимальності |
|
досягти оптимальності розв’язку ДЗ, не порушуючи його допустимості. |
Двоїстий симплекс-метод - це по суті симплекс-метод, застосований до двоїстої задачі, але котрий працює із перетвореною прямою задачею.