33. Ошибки первого и второго рода при проверке статистических гипотез. Уровень значимости критерия.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость проверить ее. Поскольку проверку производят статистич методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том» что будет принята неправильная гипотеза.

Правильное решение может быть принято также в двух случаях: гипотеза принимается; причем и в действительности она правильная; гипотеза отвергается, причем и в действительности она неверна.

Вероятность совершить ошибку первого рода принято обозначать q. Ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. 

 

34. Осн распр-ния статистич критериев. Стандартное норм распр-ние. Распр-ние Распр-ние Стьюдента. Распр-ние Фишера-Снедекора.

Нормальное распределение – одно из самых распространенных в статистической практике. Функция Ф (х) стандартного нормального распределения (с нулевым средним и единичной дисперсией) задавается формулой , где 

Распределение   Рассмотрим N независимых стандартных нормальных случайных величин X1,…, Xn,…, XN с нулевым мат. ожиданием и единичной дисперсией, т.е. Xn ~ N(0, 1).

Величина является случайной, распределение которой носит название  . Это распределение зависит от одного параметра – N, который называется числом степеней свободы. 

Распределение Стьюдента

Рассмотрим две случайные величины: X  – распределенную стандартно-нормально X ~ N(0, 1), и Y – распределенную по  с N степенями свободы  Y ~ χ2(N).

Случайная величина подчиняется распределению, которое носит имя Стьюдента. Это распределение зависит от одного параметра N, который также называется числом степеней свободы.

 Распределение ФишераПусть имеются две независимые случайные величины X1 и X2 , каждая из которых подчиняется распр-нию    с N1 и N2 степенями свободы, т.е. X1 ~ χ2(N1) и X2 ~ χ2(N2).

Случайная величина подчиняется распр-нию, кот носит имя Фишера. Это распр-ние зависит от двух параметров N1 и N2, которые также называются числами степеней свободы. 

20.  Двумерные случ велич. Числ хар-стики двум случ вел. Двумерной случ величиной наз систему из двух случайных величин  , для которой опр-на вероятность совместного выполнения неравенств   и  , где x и y - любые действительные числа.  Функция двух переменных

определенная для любых x и y, называется функцией распределения системы двух случайных величин  .

В качестве числовых характеристик двумерных случайных величин (х,у) обычно рассматриваются начальные и центральные моменты различных порядков.

Мат ожидание произведения 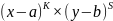называется моментом порядка k+s. Если a=b = 0, то моменты называются начальными и обозначаются  ; если a=M [x] и b=M [Y], то моменты называются центральными -  .

Начальный и центральный моменты дискретных и непрерывных с.в. (X,Y) опр-ся по формулам:

     

   

Порядком начального (центрального) момента называется сумма его индексов k + sНа практике чаще всего встречаются моменты первого и второго порядков. Начальные моменты первого порядка представляют собой мат ожидания с.в. X и Y. Точка (M[X],M[Y]) называется центром рассеивания двумерной с.в. (X,Y).

Центр моменты первого порядка равны нулю, а второго:

 

21. Условные законы распределения. Уравнение регрессии.

Рассмотрим дискретную двумерную случайную величину и найдем закон распределения составляющей Х при условии, что Y примет опр значение (например, Y = у1). Для этого воспользуемся формулой Байеса, считая гипотезами события Х = х1, Х = х2,…, Х = хп, а событием А – событие Y = у1. При такой постановке задачи нам требуется найти условные вероятности гипотез при условии, что А произошло. Следовательно, .

Таким же образом можно найти вероятности возможных значений Х при условии, что Y принимает любое другое свое возможное значение:    . Аналогично находят условные законы распределения составляющей Y:  .Уравнение регрессии. у = Му + Ry/x (х - Мx), где у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х);  х — известная средняя величина другого признака;  Ry/x — коэффициент регрессии;  Мх, Му — известные средние величины признаков x и у.