27. Статистич распр-ние выборки. Эмпирическая функция распр-ния. Полигон и гистограмма.

Cтатистическим (эмпирическим) законом распр-ния выборки, или просто статистич распр-нием выборки наз последовательность вариант х_i и соответствующих им частот n_i или относит частот w_i.

Эмпирической ф-ией распр-ния называют ф-цию F*(x), опред-щую для каждого значения x относ частоту события X<x.

По опр-нию: , где 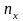- число вариант, меньших x; x- объём выборки.

Св-ва эмпирической функции распр-ния:

1) Значение эмпирич функции принадлежат отрезку [0;1]

2) F*(x)- неубывающая функция

3) если 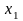- наименьшая варианта, то F*(x)=0 при x≤ ; если 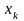- наибольшая варианта, то F*(x)=1 при x> .

Основные графики вариационного ряда: полигон и гистограмма.Полигоном частот называют ломаную, отрезки которой соединяют точки .

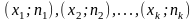Для построения полигона частот на оси абсцисс откладывают варианты х₂, а на оси ординат – соответствующие им частоты n_i. Точки (х_i,n_i) соединяют отрезками и получают полигон частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, одна из сторон которых - частичные интервалы с длиною h, другая- плотность частоты.

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h. Площадь i-го частичного прямоугольника равна h•n_i/h=n_i - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

28. Выборочная средняя и выборочная дисперсия.

Для того чтобы охарактизировать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения вводят сводную характеристику–выборочную дисперсию. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения если все значения признака выборки объема nразличны, то если же значения признака имеет соответственно частоты 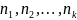причем т.е. выборочная дисперсия есть средняя взвешаная квадратов отклонения с весами , равными соотв-щим частотам. Кроме дисперсии для хар-ики рассеяния значений признака выборочной сов-сти вокруг своего сред значения пользуются сводной хар-кой – средним квадратич отклонением. Выборочным сред квадратическим отклонением называют квадратный корень из выборочной дисперсии: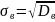

Выб средней наз.средн арифм-ое значений признака выборочной сов-сти.

1) х₁,х₂,…,х_n -все различны

n-объём выборки

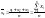
2) х₁,х₂,…,х_k -появляются с опрчастотой.

x₁– появляется n₁ раз

x₂ – n₂

x_k–n_k

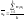
29. Точечные оценки. Смещённые и несмещенные оценки.

Точечные оценки

Точечной нзв оценку, к-рая опред-ся одним числом, например: генеральная средняя, выборочная средняя, групповая и общая средние, генеральная дисперсия, выборочная дисперсия и др.

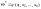
x_i – значения выборки

Несмещённая оценка — это точечная оценка, чьё математическое ожидание равно оцениваемому параметру.

Пусть   — выборка из распределения, зависящего от параметра  . Тогда оценка   называется несмещённой, если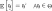 . В противном случае оценка называется смещённой, и случайная величина   называется её смещением.