17. Закон равномерного распр-ния.Хар-ки равн распр-ния

Непрерывная случайная величина имеет равномерное распр-ние на отрезке [a,b], если на этом отрезке плотность распр-ния случайной величины постоянна, а вне его равна нулю.

Для того, чтобы случайная величина подчинялась закону равномерного распр-ния необходимо, чтобы ее значения лежали внутри некоторого опр интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

18. Экспоненциальный закон распр-ния.Хар-ки

Непрерывная случайная величина X имеет показ-ный (экспоненциальный) закон распределения с параметром  , если её плотность вероятности f(x) имеет вид:

Кривая распределения  f(x)  приведена на рисунке

Теорема. Функция распределения случ величины X, распределённой по показат-му закону, есть

её мат ожидание

а её дисперсия

19. Норм распр-ние. Функц распр для норм распр. Функция Лапласа. Вер-сть попадания в зад инт.

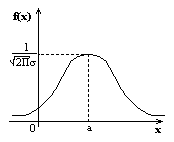
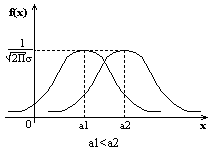
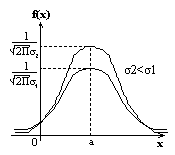
Случ вел-на ξ имеет нормальное (Гауссовское) распр-е с параметрами a и σ (σ >0), если имеет место след плотность распр-ния:

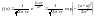
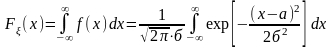
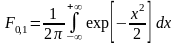
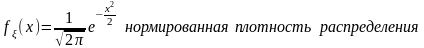
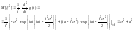
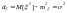
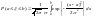
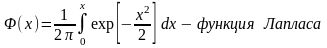
Свойства:

1. F_a,σ ²(x)=F_0,1((x-a)/σ)

xR

2. ξ (x₁, x₂)

P(x₁≤ξ≤ x₂)=Ф((x₂-a)/σ) – Ф((x₁-a)/σ)

3. Ф-цияраспрсл вел-ны ξ, распред-ой по норм закону, выражается через ф-цию Лапласа по формуле:

F_ξ(x)=½+Ф((x-a)/σ)

Вер-ть попадания нормально распределенной случайной величины на заданный интервал:

25. Математическая статистика. Основные понятия.

Мат статистика- раздел мат-тики, изучающий мат-ские методы сбора, систематизации, обработки и интерпретации результатов наблюдений с целью выявления статис-ких закономерностей. Мат статистика опирается на теорию вер-тей. Если теория вер-тей изучает закономерности случайных явлений на основе абстрактного описания действительности, то мат статистика оперирует непосредственно результатами наблюдений над случайным явлением, представляющими выборку из некоторой конечной или гипотетической бесконечной ген сов-сти. Используя результаты, полученные теорией вер-тей, мат статистика позволяет не только оценить значения искомых хар-стик, но и выявить степень точности получаемых при обработке данных выводов.

Осн понятия мат статистики:

Ген сов-сть – все множество имеющихся объектов.

Выборка – набор объектов, случайно отобранных из ген сов-сти.Виды6 повторная, бесповторная)

Объем ген сов-сти N и объем выборки n – число объектов в рассматривае-мой сов-сти.

Виды выборки:

26. Ген совокупность и выборка. Хар-тики выборки.

В мат статистике понятие ген сов-сти трактуется как сов-сть всех мыслимых наблюдений, кот могли бы быть произведены при данном реальном комплексе усл.

Выборочная сов-сть-сов-сть случайно отобранных объектов. Выборка, применяется, прежде всего, в тех случаях, когда сплошное наблюдение вообще невозможно.

Виды выборки: вероятностные и невероятностные.

Вероятностная выборка:

1. Простая вероятностная выборка:

- простая повторная выборка. Использование такой выборки основывается на предположении, что каждый респондент с равной долей вер-ти может попасть в выборку.

- простая бесповторная выборка.

2. Систематическая вероятностная выборка. Является упрощенным вариантом простой вероятностной выборки.

3. Серийная вероятностная выборка.

4. Районированные выборки

5. «Удобная» выборка Процедура «удобной» выборки состоит в установлении контактов с «удобными» единицами выборки.

Невероятностные выборка (отбор в такой выборке осущ-ется не по принципам случ-сти, а по субъективным критериям- доступности, типичности, и т.д.:

1.Квотная выборка- выборка строится как модель , кот воспроизводит структуру ген совсти в виде квот изучаемых признаков.

2. Метод снежного кома.

3. Стихийная выборка.