12. Плотность распр-ния и ее свойства. Вероятностный и геометр смысл плотности распр-ния.

Плотностью распр-ния вер-тей непрерывной С.В. называют первую производную от ф-ии распр-ния: f(x)=F(x)

Св-ва:1)плотность распр-ния неотриц.,т.е.f(x)>=0

2)вер-ть попадания непрерывнрой С.В. в интервал(а,в)равна интервалу от ее плотности вер-ти в пределах от а до в P(a<x<b)=

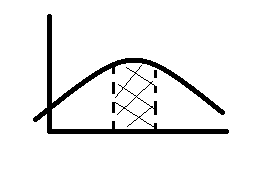
Геометрически,полученная вер-ть равна S фигуры ограниченной сверху кривой распр-ния и опирается на отрезок ав

16.Непрерывная случайная величина. Числовые характеристики непрерывных случайных величин.

Непрерывная СВ – это СВ имеющая бесконечное несчетное множество значений, покрывающая некоторый отрезок числовой оси.

Закон распр-ния СВ – это всякое соотношение устанавливающее связь между возможными значениями СВ и соответствующими ими вероятностями.

Мат ожиданием  н с в Х, возможные значения кот принадлежат отрезку [a,b], наз-ся опр интеграл

Дисперсией н с в наз-ся матожидание квадрата ее отклонения.

Средним квадратичным отклонением наз-ся квадратный корень из дисперсии.

14. Дисперсия и среднее квадратичное отклонение случайной величины и ее свойства.

ДисперсиейD(x) С.В.Х. наз-ся математическое ожидание квадрата ее отклонение от математического ожидания D(x)=M[(x-

Если С.В. дискретная с конечным числом значений,то

D(x)=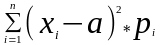 ,где а= М(х)

Если С.В.Х дискретная с бесконечно счетным, множеством значений, тогда дисперсия D(x)=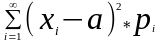 ,a=M(x),если ряд в правой части сходится

Среднимквадратическим отклонением 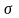(х) С.В.Х. наз-ся число

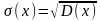
Замечание:Мат.ожидание М(х) характеризует среднее значение С.В.

Дисперсия D(x)характеризует квадратичное отклонение С.В. от среднего значения:

Св-ваD(x): 1)D(c)=0: 2)D(k*x)= *D(x)

Док-во:D(k*x)=M =

M =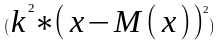

3)дисперсия D(x+-y)=D(x)+D(Y)

4)D(x)=M(x²)-(M(x))²

Док-во:D(x)=M(x-M(x))²)=M(x²-2x*M(x)+M²(x))=M(x²)-2M(x)*M(M(x))+M(M²(x))=M(x²)-2M(x)*M(x)+M²(x)=M(x²)-M²(x)

M(x) M²(X)-пост величины

15. Мат ожидание и дисперсия числа появления события в независимых опытах.

Пусть производится n независимых опытов, вер-ть появления соб в каждом из которых равна Р. Число появлений события в этих n опытах явл-ся случайной величиною Х распределённой по биномиальному закону. Число   появления события в n опытах состоит из числа появлений события в отдельных опытах, т.е.

где   имеет закон распр-ния (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).

	0	1
Р	1-р	р

Поэтому

или

т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вер-ть появления события в одном опыте.

Производится n независимых испытаний и вер-ть появления события в каждом испытании равна р. Выразим, как и прежде, число появления события Х через число появления события в отдельных опытах

Так как опыты независимы, то и связанные с опытами случайные величины   независимы. А в силу независимости   имеем

	0	1
Р	1-р	р

 

 

 

 Но каждая из случайных величин имеет закон распр-ния и  , поэтому по опр дисперсии

,

где q=1-p

В итоге имеем  , 

Среднее квадратическое отклонение числа появления событий в n независимых опытах равно  .

13. Мат ожидание случайной величины и его св-ва.

Мат ожиданием(средним значением)называют сумму следущего ряда,если он сходится М(х)=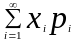

Св-ва М(х):1)М(с)=с:2)М(к*х)=к*М(х),к-постоянная величина,К=const

Док-во:М(К*Х)=

3)Математическое ожидание

M(x+-y)=M(x)+-M(y)

M(x*y)=M(x)*M(y)

M[x-M(x)]=0