7. Повторн независим испытания.Ф-ла Бернулли.

Пусть производится серия из n независимых испытаний и в каждом испытании событие А наступает с одной и той же вер-тью P(A)=p и не наступает с вер-тью 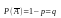. Условно появление события А наз-ся «успехом», а не появление - «неудачей». Испытания называются независимыми, если исход каждого последующего не зависит от исходов предыдущих испытаний. Последовательность независимых испытаний такого рода наз-ся схемой Бернулли. Вер-ть того, что в n независимых испытаниях событие А произойдет ровно m раз – P_n(m). Тогда имеет место формула Бернулли: P_n (m)= .

Док-во: Рассмотрим серию из n испытаний, в которых событие А произошло m раз: .Вычислим вер-ть этого произведения: P (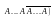 = =p^mq^{n – m}. P_n (m)= .

8. Формула Пуассона и условия ее применимости.

Исп-ние формулы Бернулли при больших n и m вызывает трудности из-за громоздких вычислений => возникает необходимость в отыскании вер-ти 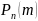обеспечивающих необходимую точность.

Т-ма: если число испытаний неограниченно увеличивается n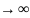 и вер-ть р наступления соб.А в каждом испытании уменьшается р , но так что их произведение n*p остается величиной постоянной (λ=np=const), то вер-ть

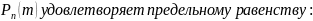
Док-во: λ=np =>p=λ/n подставляем это равенство в формулу:

= = =

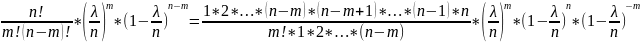Перейдем к пределу в обеих частях неравенства при n :

,

=>

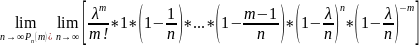
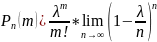
Формулу Пуассона применяют обычно когда n≥50, np≤10

9. Понятие случ вел-ны.Закон распр-ния дискретной случайной величины. Графич предст.

СВ- это переменная, кот в рез-те испытания в зав-сти от случая принимает одно из возможного множества своих значений. ДСВ – это СВ с конечным или бесконечным, но счетным множеством её значений.

Закон распр-ния СВ – это всякое соотношение устанавливающее связь между возможными значениями СВ и соответствующими ими вероятностями. Говорят, что СВ распределена по данному закону или подчинена этому закону распр-ния.

ЗАКОН распр-ния ДСВ может быть задан в виде таблицы:

х1	х2	…	хn
p1	p2	…	pn

Х:- ряд распр-ния ДСВ,где, х_1, х_2,…, х_n– возможные значения СВ, в порядке возрастания

p₁, p₂,..., p_n– соответствующие им вер-ти.

Очевидно, что суммы вер-тей p_i=1

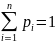
Т.к.соб Х=х, х=1,…,х= х_n образуют полную группу соб.

Закон распр-ния дискретной случайной величины может быть представлен в виде многоугольника

При этом сумма все ординат многоугольника распр-ния представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

11. Функция распр-ния и ее св-ва. Вер-ть попадания случайной величины на заданный интервал.

Ф-я распр-ния с.в.Х. наз-ся ф-я F(x)выражающая для каждого Х вер-ть того,что примет значение: F(x)=P(x<x)

Ф-я F(x) наз-ся интегральная ф-я распр-ния.Св-ва ф-ииF(x):

1)0<=F(x)<=1;2)F(x)-неубыв.ф-я на всей числовой оси.;

3)

4)P(x1<=x<=x2)=F(x2)-F(x1)

График:составим ф-ю распр-ния F(z)

1)z<=-1следовательно F(z)=P(z<z)=0

2)-1<z<=0след-ноF(z)=P(z<z)=P(z=-1)=0,08;

3)0<z<=1cлед.F(z)=P(z<z)=P(z=-1)+P(z=0)=0,34

4)1<z<=2 F(z)=p(Z<z)=P(Z=-1)+P(Z=0)+

P(Z=1)=0,08+0,26+0,22=0,56

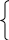
0,08;-1<z<=0

F(X)= 0,34;0<z<1

0,56;1<z<=2

0,76;2<z<=3

0,96;3<z<=4

1;z>4

Вер-ть того, что значение дискретной случайной величины F_x (x) попадает в интервал (a, b), равнаяP(a < x < b) = F_x (b) -F_x (a), вычисляется по формулам:

Если a= -  , то   ,

если b=  , то .