
- •1.Предмет теор вер. Понятие случайного события.
- •2. Осн типы событий.Алгебра событий.
- •4. Теорема сложения вер-тей.
- •3. Понятие вер-ти соб. Клас,стат,геометр опр вер-ти.
- •3. Геометрическая вер-ть
- •7. Повторн независим испытания.Ф-ла Бернулли.
- •11. Функция распр-ния и ее св-ва. Вер-ть попадания случайной величины на заданный интервал.
- •12. Плотность распр-ния и ее свойства. Вероятностный и геометр смысл плотности распр-ния.
- •16.Непрерывная случайная величина. Числовые характеристики непрерывных случайных величин.
- •14. Дисперсия и среднее квадратичное отклонение случайной величины и ее свойства.
- •17. Закон равномерного распр-ния.Хар-ки равн распр-ния
- •18. Экспоненциальный закон распр-ния.Хар-ки
- •19. Норм распр-ние. Функц распр для норм распр. Функция Лапласа. Вер-сть попадания в зад инт.
- •25. Математическая статистика. Основные понятия.
- •27. Статистич распр-ние выборки. Эмпирическая функция распр-ния. Полигон и гистограмма.
- •28. Выборочная средняя и выборочная дисперсия.
- •29. Точечные оценки. Смещённые и несмещенные оценки.
- •30. Метод моментов и метод наибольшего правдоподобия для точечных оценок.
- •32. Статистические гипотезы. Проверка гипотез. Понятие стат критерия.
- •33. Ошибки первого и второго рода при проверке статистических гипотез. Уровень значимости критерия.
- •34. Осн распр-ния статистич критериев. Стандартное норм распр-ние. Распр-ние Распр-ние Стьюдента. Распр-ние Фишера-Снедекора.
- •22. Зависимые и независимые случайные величины. Ковариация и корреляция.
- •23. Закон больших чисел и его след-вие. Нер-ство Чебышева.
1.Предмет теор вер. Понятие случайного события.
Теор вер – это математич наука,изучающая закономерности,присущие массовым случ явлениям. При этом изуч явл-ния рассматр-ся в абстрактной форме,независимо от их конкретной природы.Предметом изучения тер вер яв-ся математические модели случайных событий.
Случайным событием (просто событием) наз-ся любой факт, кот в результате может произойти или не произойти. Примеры случ событий: выпадение герба при подбрасывании монеты,выйгрыш в лотереюи тд.
Два события А и В называются несовместными, если наступление одного исключает появление другого. (Пример: соб.А – студент получил 5 на экзамене, соб.В – этот же студент получил 4 по этому же предмету. Соб.А и В несовместные, т.к. не могут произойти при одном исходе испытаний.)
Два события А и В называются совместными, если они могут произойти при одном исходе испытаний. (Студент получил 5 по одному предмету и 4 по другому)
2. Осн типы событий.Алгебра событий.
Два события А и В называются несовместными, если наступление одного исключает появление другого. (Пример: соб.А – студент получил 5 на экзамене, соб.В – этот же студент получил 4 по этому же предмету. Соб.А и В несовместные, т.к. не могут произойти при одном исходе испытаний.)
Два события А и В называются совместными, если они могут произойти при одном исходе испытаний. (Студент получил 5 по одному предмету и 4 по другому)
Событие наз-ся достоверным, если в результате испытания оно обязательно должно произойти.
Событие наз-ся невозможным, если в результате испытания оно вообще не может произойти. (Пример: в партии изделия все стандартные. Соб.А – извлечение стандартного изделия, соб.В – извлечение брака. А – достоверное, В – невозможное)
События называются равновозможными, если в результате испытания по условиям симметрии не одно из этих событий не является объективно более возможным.(Пример: пусть происходит подбрасывание монеты. Соб.А- орел, соб.В – решка)
Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них.
События образуют полную группу, если они являются единственно возможными и несовместными исходами испытания.
Два несовместных события, из которых одно должно произойти называются противоположными.
Соб. А1 и А2нзв равными, если осуществление соб.А1 влечет за собой осуществление соб. А2 и наоборот.А1=А2
Суммой
(объединением)
соб. А и B
нзв соб.C,
к-рое означает осущ-е хотя бы одного из
соб. А или B.![]() Произведением
(пересечением)
соб. А и Bнзв
соб. C,
к-рое означает, что одновременно осущ-ся
и А и B.
Произведением
(пересечением)
соб. А и Bнзв
соб. C,
к-рое означает, что одновременно осущ-ся
и А и B.![]() Разностью
соб. А и Bнзв
соб. C,
к-рое означает, что происх. соб. А, но не
происх. соб. B.
Разностью
соб. А и Bнзв
соб. C,
к-рое означает, что происх. соб. А, но не
происх. соб. B.
![]() Соб.
Ā нзв противоположным
по отношению к соб. А, если оно состоит
из элемент.соб., не входящих в соб.А, но
входящих в простр-во элемент.соб. Ω.
Соб.
Ā нзв противоположным
по отношению к соб. А, если оно состоит
из элемент.соб., не входящих в соб.А, но
входящих в простр-во элемент.соб. Ω.![]()
Ā=Ω\А,А+Ā=Ω
Несовместные события:
![]()
А∙B=Ø
Свойства операций:
1.Ω+А=Ω 2.Ω∙А=А
3.А∙А=А 4.А+Ø=А
5.А∙Ø=Ø 6.(А\В)∙(В\А)=Ø
7.А+Ā=Ω 8.А∙Ā=Ø
9. 10.
10.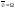
11. 12.
12.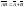
13.А+В=В+А 14.А∙В=В∙А
15.(А+В)+С=А+(В+С) 16.(А∙В)∙С=А∙(В∙С)
17.С(А+В)=СА+СВ 18.А+ВС=(А+В)(А+С)
