Лекція 23

16.5. Виведення рівнянь Лагранжа іі-го роду

Скористаємось загальним рівнянням динаміки

,

переписавши його у вигляді

.

(23)

Перейдемо в останньому рівнянні до узагальнених координат, беручи до уваги вираз

,

або

.

(24)

Перейдемо до узагальнених координат у тих членах рівняння (23), що залишилися. Спочатку перетворимо їх наступним чином:

.

Перетворимо потім вираз, який стоїть у дужках, з урахуванням тотожностей Лагранжа за формулою диференціювання скалярного добутку двох векторів ( ):

(тут , ; далі використаємо у члені 1 першу тотожність Лагранжа, змінюючи також у всіх доданках порядок виконання операцій додавання і взяття похідних)

.

Оскільки являє собою кінетичну енергію механічної системи, остаточно отримаємо

.

Таким чином,

.

(25)

На підставі (24) і (25) загальне рівняння динаміки (23) набуває вигляду

.

(26)

Оскільки варіації узагальнених координат є довільними і незалежними між собою, то, щоб співвідношення (26) виконувалось за будь-яких необхідно, щоб одночасно обертались в нуль всі коефіцієнти біля них:

.

(27)

Рівняння (27) називаються рівняннями Лагранжа ІІ-го роду. Вони мають ряд переваг над рівняннями Ньютона, а саме:

• їхня кількість мінімальна і дорівнює числу степенів вільності (на відміну від рівнянь Ньютона, яких для системи із точок треба скласти );

• реакції ідеальних в’язей в рівняння Лагранжа ІІ-го роду не входять;

• їх зручно застосовувати для розв’язання задач, оскільки методика є добре алгоритмізованою;

• форма запису цих рівнянь не залежить від конкретного вибору системи узагальнених координат.

Методика застосування рівнянь Лагранжа ІІ-го роду (27) полягає в наступному.

1. Визначити число степенів вільності системи і вибрати узагальнені координати.

2. Обчислити кінетичну енергію системи за аналізом рухів тіл, що її складають, і представити її як функцію узагальнених координат і швидкостей.

3. Обчислити узагальнені сили за одним із трьох вказаних вище методів.

4. Підставити в рівняння Лагранжа ІІ-го роду функцію і узагальнені сили і скласти диференціальні рівняння руху системи.

5. Проінтегрувати рівняння руху і знайти кінематичний закон руху системи.

6. Якщо необхідно визначити реакції в'язей, то можна застосувати рівняння Ньютона (ІІ-й закон Ньютона), принцип Д'Аламбера або теорему про зміну кінетичної енергії, інші теореми динаміки.

7. Проаналізувати отриманий розв’язок.

Наведемо застосування цієї методики для отримання диференціальних рівнянь руху математичного маятника і колеса.

16.6. Рівняння Лагранжа іі-го роду для консервативних систем

Якщо всі сили, що діють на механічну систему, є потенціальними, то така система називається консервативною. Встановимо вид рівнянь Лагранжа ІІ-го роду для таких систем.

В цьому разі узагальнені сили визначаються через потенціальну енергію механічної системи, тобто

.

Підставляючи цей вираз в рівняння Лагранжа ІІ-го роду (27), отримуємо

.

(28)

Оскільки потенціальна енергія механічної системи є функцією тільки узагальнених координат, тобто , то частинна похідна від цієї функції за узагальненими швидкостями дорівнює нулю. Тому вираз (28) можна записати у вигляді

.

(29)

Введемо позначення

.

Функція називається функцією Лагранжа або кінетичним потенціалом механічної системи.

За допомогою функції Лагранжа рівняння (29) набувають наступної форми запису

.

Ці рівняння називаються рівняннями Лагранжа ІІ-го роду для консервативних систем.

Якщо на механічну систему окрім потенціальних сил діють які-небудь інші (непотенціальні) сили, то рівняння руху такої системи набувають вигляду

,

де - непотенціальні узагальнені сили.

Задача

Визначити лінійне прискорення тягаря маси , який піднімається по похилій (кут нахилу до горизонту ) гладенькій площині за допомогою шківа, що обертається навколо своєї осі прикладеною двигуном парою сил з моментом (рис. 1). Шків являє собою суцільний однорідний диск маси та радіуса . Шків і тягар з’єднані ідеальним тросом.

Дано: , ; , , .

Знайти .

Рис. 1

Р о з в ’ я з а н н я

Діємо за наведеною вище методикою.

1. Визначаємо число степенів вільності системи - ; за узагальнену координату вибираємо переміщення тягаря по похилій площині: .

2. Обчислюємо кінетичну енергію систему як функцію узагальненої координати і швидкості. Оскільки тягар рухається поступально, то його кінетична енергія дорівнює . Шків обертається навколо нерухомої осі, тому його кінетична енергія буде мати такий вираз: . Отже повна кінетична енергія системи складатиме: .

3. Узагальнену силу будемо обчислювати за другим способом. Для цього надамо тягарю можливе переміщення . Тоді можливе переміщення шківу буде . Знайдемо можливу роботу всіх активних сил, прикладених до тіл, що входять до системи, на відповідних можливих переміщеннях їх точок прикладання . Отже узагальнена сила є .

4. Підставляємо в рівняння Лагранжа ІІ-го роду знайдену кінетичну енергію та узагальнену силу і складаємо диференціальне рівняння руху системи: , звідки визначаємо шукане прискорення: або .

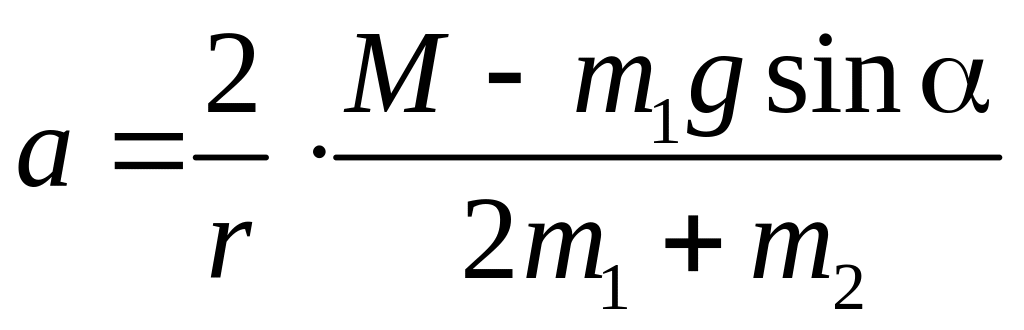Зауважимо знову, що отриманий вираз є диференціальним рівнянням руху розглядуваної механічної системи (математичною моделлю її руху) за переміщенням .

1 Зауважимо, що неутримуючу в’язь називають ще односторонньою, а утримуючу – двосторонньою.

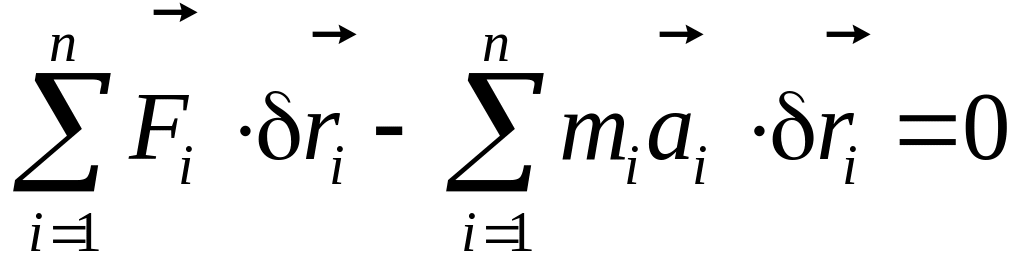61