Тема 4.2. Принципи механіки

Лекція 21

14. Принцип можливих переміщень

14.1. Загальне рівняння статики

Для рівноваги механічної системи, що підкорена ідеальним утримуючим стаціонарним в’язям, необхідно і достатньо, щоб дорівнювала нулю можлива робота активних сил на будь-яких можливих переміщеннях точок системи із розглядуваного положення рівноваги.

(Нагадаємо, що положенням статичної рівноваги називається таке положення механічної системи, в якому вона буде знаходитися весь час, якщо в початковий момент часу вона знаходилась в цьому положенні і швидкості всіх її точок дорівнювали нулю).

Д о в е д е н н я

Необхідність

Нехай механічна система, що складається з матеріальних точок, знаходиться в рівновазі і підкоряється утримуючим стаціонарним ідеальним в’язям. Застосувавши аксіому про звільнення від в’язей, замінимо дію в’язей відповідними реакціями. Тоді на систему будуть діяти активні сили і реакції в’язей . Як відомо (із розділу 1), механічна система знаходиться в рівновазі, якщо кожна точка цієї системи знаходиться в рівновазі. Із цього випливає, що для кожної точки механічної системи виконується умова:

,

(1)

де - рівнодійна всіх активних сил, що діють на -ту точку;

- рівнодійна всіх реакцій в’язей, що діють на -ту точку.

Надамо всім точкам даної механічної системи можливі переміщення , тоді помножуючи скалярно вирази (1) на і додаючи отримані рівняння, матимемо

.

(2)

Беручи до уваги постулат ідеальних в’язей ( ), отримаємо

,

(3)

або

,

(4)

що і треба було довести.

Вирази (3) і (4) називаються загальним рівнянням статики, вони є також математичним виразом принципа можливих переміщень у разі утримуючих в’язей.¹

Зауважимо, що неутримуючу в’язь називають ще односторонньою, а утримуючу – двосторонньою.

Достатність

Припустимо, що виконується умова (3). Покажемо, що при цьому механічна система, яка підкорена утримуючим ідеальним в’язям, знаходиться в рівновазі.

Припустимо, що механічна система починає рухатися з деякого моменту часу. Обмежимось випадком стаціонарних в’язей (тоді дійсні переміщення входять у число можливих). Застосовуючи теорему про зміну кінетичної енергії системи, враховуючи, що , і беручи до уваги те, що , отримаємо

,

де - ті можливі переміщення точок системи, з якими співпадають дійсні переміщення . Однак остання нерівність суперечить умові (3).

Таким чином теорема доведена.

Розглянемо випадок ідеальної неутримуючої в’язі. Нагадаємо, що у разі ідеальної утримуючої в’язі можливе переміщення знаходиться у дотичній площині (див. рис. 8).

Рис. 8

В нашому випадку (неутримуючої в’язі), якщо в’язь є стаціонарною, тоді можливими переміщеннями будуть: переміщення , розташоване у дотичній площині , і переміщення , напрямлене вздовж реакції в’язі. Розглянемо роботу реакції в’язі на можливих переміщеннях і : , де через постулат ідеальних в’язей.

Таким чином, з виразу (2) у разі неутримуючих в’язей матимемо

.

(5)

Співвідношення (5) є математичним виразом принципа можливих переміщень для неутримуючих в’язей.

Задача 1

На гладенькій похилій площині лежить тягар вагою (див. рис. 9). Тягар утримується ниткою, перекинутою через блок , до іншого кінця якої прикріплено тягар вагою .

При якому куті нахилу площини до горизонту тягарі будуть знаходитися в рівновазі?

Рис. 9

Р о з в ’ я з а н н я

Дана механічна система, що складається з двох тіл і , є невільною. В’язями є похила площина і нитка, які розглядаються як ідеальні. Застосуємо для розв’язання задачі основне рівняння статики (3).

Активними силами є і .

Встановимо можливі переміщення тіл і , розглядаючи їх як матеріальні точки, які співпадають з центрами мас тіл.

Перша в’язь – похила площина – допускає переміщення тягаря вздовж неї. Позначимо це можливе переміщення .

Друга в’язь – нитка – допускає вертикальне переміщення тягаря . Введемо можливе переміщення тягаря - (нитка перекинута через нерухомий блок, який лише змінює напрямок можливого переміщення, тобто, якщо тягар рухається вздовж площини вниз, то тягар піднімається вверх).

Вираз можливої роботи сил і на відповідних можливих переміщеннях і має вигляд

,

звідки, помітивши, що (адже нитка є ідеальною, тобто нерозтяжною), отримаємо

.

(6)

Оскільки рівняння (6) повинно виконуватися на всіх можливих переміщеннях , тому

.

Задача 2

Два тягаря і мають вагу кожний і зв’язані нерозтяжною мотузкою, перекинутою через невагомий блок (див. рис. 10). Коефіцієнт тертя ковзання між тягарями та гранями і призми дорівнює . Кути призми дорівнюють: ; .

Нехтуючи тертям мотузки по блоку, знайти кут , при якому тягар починає спускатися.

Рис. 10

Р о з в ’ я з а н н я

Використаємо для розв’язання задачі загальне рівняння статики (3).

Активними силами є сили ваги і , а також сили тертя ковзання і . Нормальні складові реакцій граней призми не показані, оскільки їх робота на можливих переміщеннях тіл даної системи дорівнює нулю.

Накладені на систему в’язі (мотузка та грані призми) допускають тільки переміщення тягарів по гранях. Отже можливим переміщенням тягаря вздовж буде . Таке ж за величиною можливе переміщення буде мати і інший тягар , оскільки нерозтяжна мотузка, що з’єднує обидва тягаря, перекинута через невагомий блок з нерухомою віссю обертання (він змінює лише напрямок можливого переміщення, а величина його залишається сталою), тобто .

Сили тертя ковзання можна визначити через сили нормального тиску:

, .

Тоді, застосовуючи загальне рівняння статики, отримаємо:

,

звідки матимемо

.

14.2. Умови рівноваги вільного і невільного твердого тіла

Розглянемо вільне тіло, до якого прикладена система сил (див. п. 9.6, присвячений обчисленню елементарної роботи сил, що прикладені до твердого тіла, яке здійснює вільний рух).

Надамо можливе переміщення точці, що називається полюсом (т. ), і можливе кутове переміщення , яке відповідає повороту тіла навколо полюса.

Складемо вираз можливої роботи сил, що прикладені до даного тіла, на вказаних можливих переміщеннях:

.

Із принципу можливих переміщень випливає, що , тобто

.

(7)

Оскільки і незалежні, для виконання умови (7) необхідно і достатньо, щоб одночасно виконувалися такі умови:

.

(8)

Це є умови рівноваги вільного тіла у векторній формі, де - головний вектор, а - головний момент зовнішніх сил, обчислений відносно полюса . У скалярній формі вирази (8) набудуть вигляду

Рис. 11

Для тіла, що обертається навколо нерухомої осі, якщо вибрати полюс на осі обертання, матимемо: , а вираз (7) перетвориться на , або , звідки випливає, що , або . (9) Вираз (9) є умовою рівноваги тіла з нерухомою віссю обертання.

Лекція 22

15. Принцип д’Аламбера-Лагранжа (загальне рівняння динаміки)

Розглянемо механічну систему, що складається з матеріальних точок (і знаходиться в русі).

Застосуємо ІІ-й закон Ньютона, доповнений аксіомою про звільнення від в’язей:

.

Якщо застосувати принцип Д’Аламбера для кожної точки системи, то отримаємо

,

(10)

де - даламберова сила інерції.

Надамо кожній точці можливе переміщення і помножимо на нього скалярно кожне рівняння (10), після чого знайдемо суму цих рівнянь за всіма точками системи:

.

(11)

Через те, що система підкорена ідеальним утримуючим (двостороннім) в’язям, другий доданок у формулі (11) дорівнює нулю, і тоді маємо

- загальне рівняння динаміки, яке є також математичним записом принципу Д’Аламбера-Лагранжа у разі утримуючих в’язей.

Принцип Д’Аламбера-Лагранжа: при русі механічної системи, яка підкорена ідеальним утримуючим в’язям, необхідно щоб сума можливих робіт активних сил і сил інерції на будь-яких можливих переміщеннях точок механічної системи дорівнювала нулю:

.

У разі неутримуючих ідеальних в’язей запис принципу Д’Аламбера-Лагранжа має вигляд:

.

16. Рівняння Лагранжа іі-го роду

16.1. Узагальнені координати

У якості незалежних координат, які однозначно визначають положення механічної системи, виберемо -координат з числа -декартових координат і позначимо їх , або ( ). Тоді декартові координати є функціями незалежних координат і, можливо, часу. Виразимо через координати всіх точок даної системи наступним чином:

(12)

Візьмемо варіації лівої і правої частин виразу (12), беручи до уваги, що при варіюванні час вважається сталим:

(13)

Із рівнянь (13) випливає, що всі можливих переміщень в декартових координатах виражаються через незалежних координат, число яких збігається з числом степенів вільності.

Незалежні змінні ( ), які однозначно визначають положення точок даної системи, називаються узагальненими координатами.

Висновок: число степенів вільності механічної системи дорівнює числу узагальнених координат і дорівнює числу незалежних можливих переміщень, які можна надати точкам механічної системи з даного положення у фіксований момент часу.

Рівняння (12) показують зв’язок декартових координат з узагальненими.

Таким чином введення незалежних змінних - узагальнених координат - дозволяє не розглядати рівняння голономних в’язей.

Узагальнені швидкості – перші похідні за часом від відповідних узагальнених координат: .

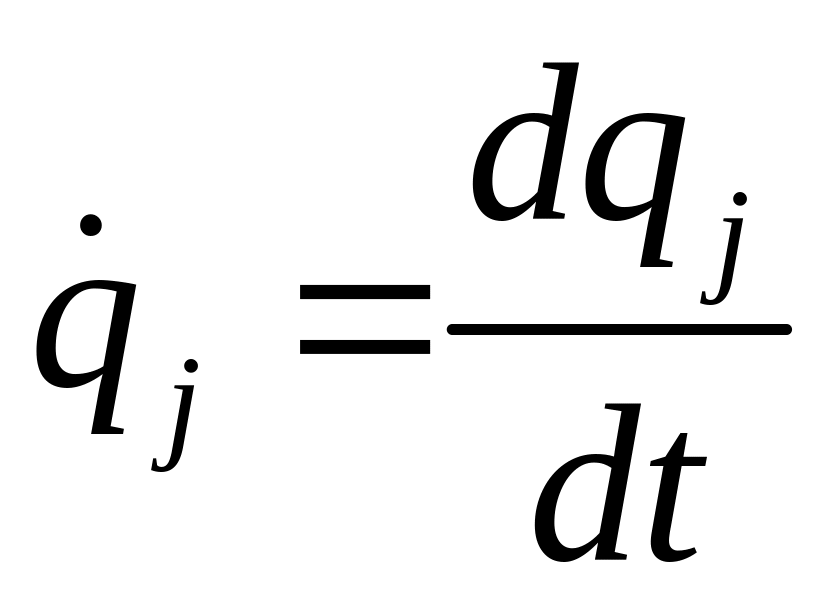Знайдемо зв’язок між узагальненими і звичайними швидкостями . Оскільки , тому матимемо:

,

або остаточно

.

Цей вираз показує зв’язок між лінійними і узагальненими швидкостями точок механічної системи.