Этап №6 Функции Подбор параметра и Поиск решения. Структура проведения занятий

Вводная часть 5 мин.

Практическая работа 80 мин.

• выполнение упражнений 1,2 на использование

функции Подбор параметра 30 мин.

• выполнение упражнений 3,4 на использование

функции Поиск решения 30 мин.

Самостоятельная работа 20 мин.

Заключительная часть (подведение итогов) 5 мин.

Задания для индивидуальной работы и методические рекомендации по их выполнению

На этом занятии будут изучены еще две функции программы Excel такие, как Подбор параметра и Поиск решения. Интерес к этим функциям вызван тем фактом, что кроме решения чисто математических задач, одна из них – это задача о нахождении корня уравнения F(x)=0, эти функции прекрасно справляются с экономическими задачами планирования. Дело в том, что руководитель производственного предприятия любого профиля и уровня заинтересован в рентабельности своего производства. Кроме решения производственных задач, часто нужно принимать решения по оптимальному управлению производственными или людскими ресурсами. Например, в правоохранительной деятельности это и планирование массовых операций с привлечением личного состава подразделения, организация дежурства, выполнение производственных планов в исправительно-трудовых учреждениях и т.д. Главная проблема, которую нужно решать руководителю, заключается в том, что на предприятии имеется ограниченный объем ресурсов, а планируется получить максимальную отдачу. При решении любой задачи планирования всегда есть некоторая величина, для которой нужно получить либо максимальное, либо какое-то фиксированное, либо минимальное значение. Например, планируемая прибыль должна быть максимальной, а затраты на производство продукции – минимальные. Такая величина называется Целевой функцией. Кроме целевой функции в задачах планирования всегда имеются некоторая система ограничений. Для привлечения вычислительной техники к решению поставленной задачи её необходимо описать математически. В приведенных ниже упражнениях подробно описаны примеры использования функций Подбор параметра и Поиск решения при решении конкретных задач.

Упражнение 1. Сейчас воспользуемся функцией Подбор параметра для нахождения корней квадратного уравнения . Зададим его с коэффициентами в конкретном виде

.

1. Откройте новую книгу Excel и сохраните её с именем Подбор параметра. Оформите условие задачи в соответствии с рисунком 12 и пояснениями к нему.

Рисунок 12. Оформление задачи к упражнению 1.

Здесь в ячейке С1 записано выражение для функции F(x), которое адресуется к ячейкам с соответствующими адресами. В ячейке B1 подставлено значение х, при котором вычисляется функция F(x). Функция Подбор параметра должна подобрать для этого х такое значение, при котором функция F(x) обращается в нуль.

2. Вызовите функцию Подбор параметра, выбрав в закладке Данные ► Подбор параметра и установите все значения в соответствии с рисунком 13.

После того как вы щелкните по кнопке ОК должен получиться результат показанный на рисунке 14. На нем в ячейке C1 отображено полученное значение, близкое к нулю, а в ячейке B1 - приближенное значение корня. Следует отметить, что при этом значении х₁ = – 1,0763 найденное значение функции равно нулю не точно, а лишь приближенно.

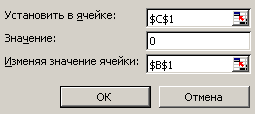
Рисунок 13. Окно функции Подбор параметра из упражнения 1.

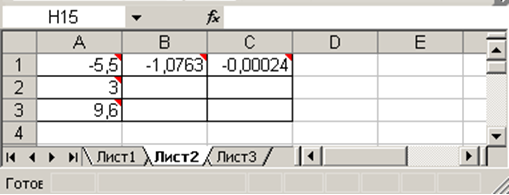
Рисунок 14. Результаты решения упражнения 1.

3. Мы нашли только один корень уравнения F(x), хотя квадратное уравнение имеет два корня. Чтобы найти другой корень уравнения нужно в ячейке В1 ввести другое ненулевое значение (см. рисунок 11), при котором функция Подбор параметра получит другое значение корня. Это новое значение в ячейке В1, должно быть подобрано в ручную. Подставьте в ячейку В1, любое положительное значение равное нескольким единицам, а затем проведите подбор корня функцией Подбор параметра. В качестве другого корня должно получиться значение х₂ = 1,621746.

Упражнение 2. Рассмотрим другой пример использования функции Подбор параметра на примере решения экономической задачи.

Предполагается, что известен размер вклада, который помещается в банк на определенный срок под проценты. Нужно вычислить коэффициент наращивания (значение, показывающее во сколько раз увеличится вклад за указанный срок) и сумму выплат в конце срока. Кроме этого необходимо также определить исходя из заданной суммы выплат необходимый размер вклада при неизменных сроке и процентной ставке. В приведенной на рис. 15 таблице в ячейке C1 указан начальный вклад в рублях. В ячейке С3 – срок, на который делается вклад. Значение процентной ставки (5% годовых) приведено в ячейке С5. Коэффициент наращения, содержащийся в ячейке С7, определялся по формуле: = (1+С5)^С3 (для возведения в степень используется функция СТЕПЕНЬ(1+С5;С3)). Сумма выплат рассчитывается в ячейке С10 по формуле = С7*С1.

Теперь предположим, что мы через то же количество лет и при фиксированных процентах хотим получить 50000 рублей. Спрашивается, какой должна быть первоначальная сумма для этого?

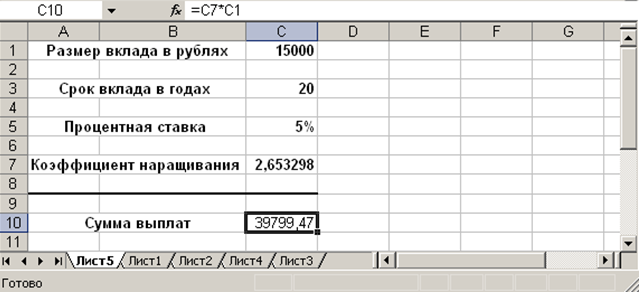
Рисунок 15. Исходная таблица к упражнению 2.

1. Перейдите на новый лист Excel. Для решения поставленной выше задачи сделайте активной ячейку С10 и откройте диалоговое окно Подбор параметра. В окно значение укажите целевое значение 50000. Далее поместите курсор в поле Изменяя значения ячейки и сделайте активной ячейку, значение которой нужно подобрать, т.е. С1.

2. После задания всех параметров нажимаем на кнопку ОК. Таким образом, мы определим первоначальную сумму вклада, при процентной ставке 5% годовых, чтобы через 20 лет получить 50000 рублей (см. таблицу ниже).

Размер вклада в рублях		18844,47
Срок вклада в годах		20
Процентная ставка		5%
Коэффициент наращивания		2,653298
Сумма выплат		50000

Упражнение 3. Рассмотрим пример использования функции Поиск решения для решения задачи оптимального управления. Постановка задачи будет состоять в следующем. Имеется предприятие, изготавливающее железные баки для воды. Бак имеет размер ребер а, b и c (смотрите рисунок 16). Предположим, что верхняя крышка бака отсутствует.

Рисунок 16. Бак для воды из упражнения 3.

Нашей задачей является спланировать изготовление такого бака, на использование которого бы ушло как можно меньше железа, и одновременно бак должен иметь как можно большую вместимость. Предположим, что на производство бака выделено прокатного железа площадью . Мы также должны задать минимальные размеры бака, например: ; . Обратите внимание на то, что эти значения на самом деле можно задать произвольными числами. Программа Поиск решения подберет значения и 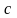сама из условия наибольшего значения для объема бака и учитывая введенные нами ограничения.

Итак, сформулируем сначала математическую постановку задачи:

объем бака V - определяется по формуле:

. (1)

По условию задачи этот объем следует свести к наибольшему значению. Таким образом, мы определяем целевую функцию, представляющую собой объем изготавливаемого бака 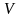. На его изготовление должно уйти как можно меньше прокатного железа. Следовательно, мы должны рассчитать площадь бака P по формуле:

. (2)

Как было уже сказано, любая задача должна содержать определенную систему ограничений. В нашем случае система ограничений имеет следующий вид:

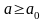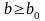, , , . (3)

Пояснения.

1. Перейдите на новый лист Excel. Оформите вашу задачу в соответствии с рисунком 17, введя в соответствующие ячейки все необходимые формулы.

2. После этого вызовите функцию Поиск решения, используя закладку Данные.

3. Установите целевую ячейку по адресу В6. В окне Изменяя ячейки выделите диапазон В2:В4. В окно Ограничения введите систему ограничений в соответствии с рисунком 18. После этого щелкните на кнопку Выполнить и сохраните найденное решение.

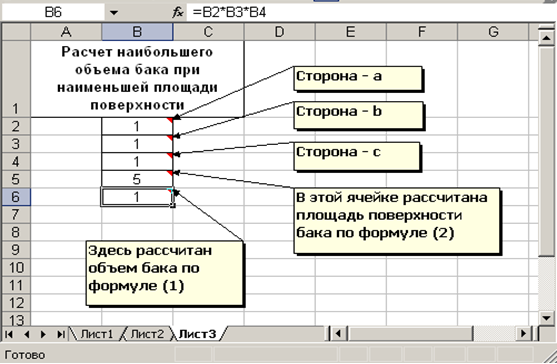
Рисунок 17. Оформление задачи из упражнения 3.

Рисунок 18. Ввод системы ограничений к упражнению 3.

Упражнение 4. На строительство дачного домика выделяется земельный участок, имеющую фиксированную площадь 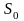=1000м². Предположим, он будет иметь прямоугольную форму со сторонами а и b. Этот участок нужно огородить забором так, чтобы на его строительство ушло как можно меньше пиломатериала.

Итак, при заданной площади участка =1000м² необходимо подсчитать его стороны а и b, при которых периметр, а следовательно и количество пиломатериала, имеют наименьшее значение.

Определим целевую функцию. В нашем случае она представляет собой периметр земельного участка и должен быть сведен к минимальному значению:

.

Определим систему ограничений на минимальные размеры сторон. Предположим, что:

а) , .

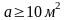Кроме того, одним из ограничений является площадь, которая должна быть равна значению . Т.е. другое ограничение состоит в том, что

б) должна быть равна 1000м².

1. По подобию предыдущего упражнения оформите задачу на новом листе Excel и рассчитайте периметр участка.

2. Используя функцию Поиск решения определите длины сторон a и b, при которых периметр наименьший, а объем имеет фиксированное значение.