1. Графические схемы циклических вычислительных процессов

Циклический вычислительный процесс - это процесс, который состоит в многократном выполнении одной и той же последовательности операций над различными значениями.

Такой процесс может быть описан циклическим алгоритмом, обладающим тем достоинством, что число предписаний в нем меньше числа операций, выполняемых в ходе реализаций. Так, например, задача вычисления функции H по формуле:

при изменении значения Е от 0 до 15 с шагом 1 описывается циклическим алгоритмом, приведенном на рис . 7.

Для организации циклической структуры можно использовать либо блочный символ “ Решение” в совокупности с символом “ Процесс”, либо специальный символ “ Модификация “. В этом случае блок-схема будет иметь вид рис.8.

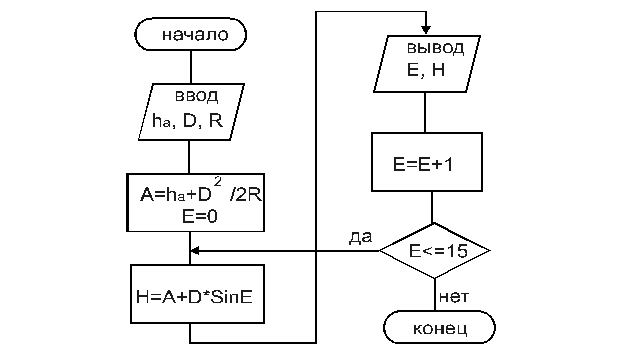
Рис.7

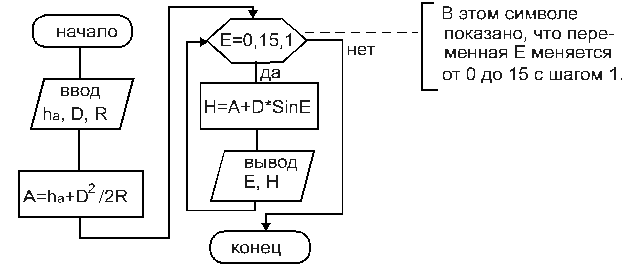
Рис. 8

Очевидно, что данная задача могла бы быть описана и линейным алгоритмом. В этом случае мы должны были бы явно записать 16 предписаний Н = А + D Sin E; вывод Е; H; E = E + 1. Ясно, что такой алгоритм потребовал бы для своей записи много времени и места в памяти ЭВМ при его реализации и кроме этого решал бы только частную задачу вычисления 16 значений Н. Кстати, на приведенной выше блок-схеме также описано частное решение задачи исследования зависимости Н = f ( E ). Для того чтобы задача решалась в общем виде, необходимо начальное значение переменной Е ( Еn ), конечное ( Ek ) и шаг изменения ( dE ) задавать в качестве переменных при вводе данных.

В этом случае блок-схема будет иметь следующий вид (рис.9 ).

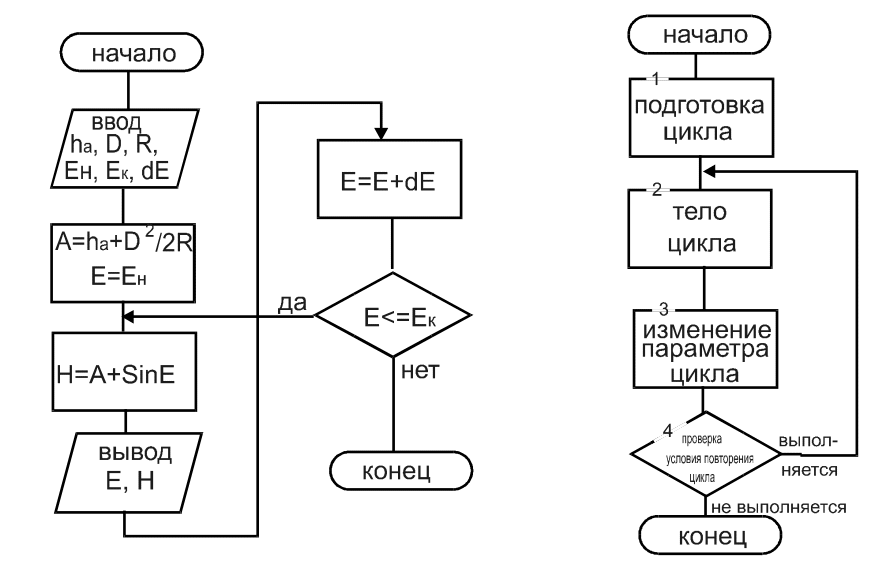Рис.9 Рис. 10

Рассмотренная задача может служить иллюстрацией того, что в циклическом алгоритме помимо группы предписаний, повторяющихся многократно до выполнения некоторых условий, называемой циклом алгоритма, имеется группа подготовительных предписаний обеспечивающих нормальную работу цикла.

Кроме того, каждому выполнению цикла ставится в соответствие некоторая величина, используемая для подготовки выполнения очередного цикла. Такую переменную величину принято называть параметром цикла (Е - для примера). В качестве параметра цикла могут использоваться аргументы вычислительных функций, счетчики числа повторений, адреса обрабатываемых данных и др.

Исходя из сказанного выше можно составить общую структуру циклического алгоритма, которая включает в себя следующие части (рис.10) : подготовка цикла ( блок 1 ), рабочая часть или тело цикла (блок 2), управление циклом (блоки 3, 4 ).

Внутри одного цикла могут находиться один или несколько других циклов. В этом случае охватывающий цикл называется внешним, а вложенные в него циклы - внутренними. Такие алгоритмы называются алгоритмами со структурой вложенных циклов. Правила организации как внешнего, так и внутренних циклов аналогичны правилам организации простого цикла.

ЭТАП 5

Продолжительность 2 часа

Учебные вопросы:

1. Методы алгоритмизации расчетных задач.

2. Примеры схем алгоритмов. Совместное проектирование ветвящихся и циклических алгоритмов.