2. Операции с множествами: объединение, пересечение, разность, симметрическая разность.

Объединением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В, т. е. принадлежат А, или принадлежат В, или принадлежат и А и В. Объединение множеств А и В обозначается через АВ. Таким образом,

С=АВ={ccA или сВ}.

Напомним, что согласно «определению» множества, если один и тот же элемент содержится и в множестве А и в множестве В, то в их объединение этот элемент включается только один раз.

Пересечением множеств А и В называется множество С, состоящее из элементов, которые принадлежат как множеству А, так и множеству В одновременно. Пересечение множеств А и В обозначается через АВ. Таким образом,

С=АВ={ccA и сВ}.

Т.е. пересечение множеств есть общая часть данных множеств.

Разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат множеству А, но не входят в множество В. Разность множеств А и В обозначается через А\В. Таким образом,

С=А\В={ccA и сВ}.

Симметрической разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат какому-то одному из множеств А или В. Симметрическая разность множеств А и В обозначается через АВ.

С=АВ= (А\В) (В\А).

Пример 3. Множество А состоит из натуральных четных чисел, множество В – из натуральных чисел, делящихся на 3. Из каких чисел состоит множество АВ? Ответ: из натуральных чисел, делящихся на 6.

Пример 4. Множество А состоит из натуральных четных чисел, множество В – из натуральных чисел, делящихся на 3, множество С – из натуральных чисел, делящихся на 12. Из каких чисел состоит множество АВС? Изобразите множества с помощью кругов Эйлера.

Ответ: из натуральных чисел, делящихся на 12.

Пример 5. Множество А состоит из натуральных чисел, делящихся на 4, множество В – из натуральных чисел, делящихся на 6, множество С - из натуральных чисел, делящихся на 15. Из каких чисел состоит множество D=АВС? Изобразите множества с помощью кругов Эйлера. Ответ: из натуральных чисел, делящихся на 60.

Пример 6. Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:

а) (А  В);

б) (С  В);

в) (А\В);

г) (С \ А)  (С \ В); 

д) (С \ А)  (В \ С);

е) (С\В)  (А\С);

ж) А  С.

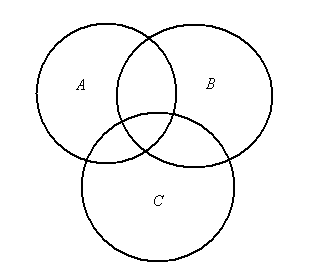
Пример 7. Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:

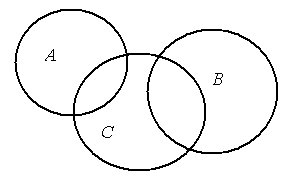
а)  (А  В) \ С;

б) (А  В)  (С  В);

в) (А  В)  (С \ В);

г) (С\В)  (А\С);

д) (А\С)  (ВС);

е) (СА) \ (В  С).

Пример 8. Даны два множества А = {1,2,3,4,5,6} и В = {3,6,9,12}. Найти объединение, пересечение, разности этих множеств.

Решение:

Объединением (суммой) множеств А и В является множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В, следовательно, A  B = {1,2,3,4,5,6,9,12}.

Пересечением (произведением) множеств А и В является множество, состоящее из всех элементов, принадлежащих обоим множествам А и В, следовательно, А  В = {3,6}.

Разностью множеств А и В является множество элементов, которые принадлежат множеству А, но не принадлежат множеству В, следовательно, А \ В = {1,2,4,5}; В \ А = {9,12}.

Симметрической разностью множеств А и В является множество элементов, принадлежащих или множеству А, или множеству В (но не обоим вместе), следовательно, А ∆ В = {1,2,4,5,9,12}.