Задание n 16 Тема: Динамика поступательного движения

Автомобиль поднимается в гору по участку дуги с увеличивающейся по величине скоростью. Равнодействующая всех сил, действующих на автомобиль, ориентирована в направлении …

4

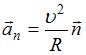Решение: Согласно второму закону Ньютона  , где  равнодействующая всех сил, действующих на тело,  его ускорение. Вектор ускорения удобно разложить на две составляющие:  . Тангенциальное ускорение  направлено по касательной к траектории в данной точке и характеризует быстроту изменения модуля скорости; нормальное ускорение  направлено по нормали к траектории в данной точке (направление 3) и характеризует быстроту изменения направления скорости. При движении по криволинейной траектории  0, при движении с увеличивающейся по величине скоростью  0 и вектор  ориентирован в направлении 5. Следовательно, вектор  , а значит, и вектор  ориентирован в направлении 4.

ЗАДАНИЕ N 17  Тема: Свободные и вынужденные колебания

Колебательный контур состоит из катушки индуктивности  конденсатора  и сопротивления  Добротность контура равна …

200

Решение: Добротность контура равна: 

ЗАДАНИЕ N 18  Тема: Сложение гармонических колебаний

Складываются взаимно перпендикулярные колебания. Установите соответствие между законами колебания точки  вдоль осей координат  и формой ее траектории. 1.  2.  3. 

1			прямая линия
2			эллипс
3			фигура Лиссажу
			cинусоида

Решение: При одинаковой частоте колебаний вдоль осей  исключив параметр времени, можно получить уравнение траектории:  . Если разность фаз колебаний  , то уравнение преобразуется к виду 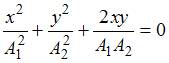 , или  , что соответствует уравнению прямо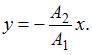й:  Если  , то  , что является уравнением эллипса. Если складываются колебания с циклическими частотами  и  , где  и  целые числа, точка  описывает сложную кривую, которую называют фигурой Лиссажу. Форма кривой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.

Задание n 1 Тема: Свободные и вынужденные колебания

Начало формы

Конец формы

Маятник совершает вынужденные колебания со слабым коэффициентом затухания  , которые подчиняются дифференциальному уравнению  Амплитуда колебаний будет максимальна, если частоту вынуждающей силы уменьшить в _____ раз(-а).

5

Решение: Дифференциальное уравнение вынужденных колебаний имеет вид  , где  коэффициент затухания,  собственная круговая частота колебаний;  амплитудное значение вынуждающей силы, деленное на массу;  частота вынуждающей силы. При слабом затухании (коэффициент затухания значительно меньше собственной частоты колебаний маятника) амплитуда колебаний будет максимальна, если частота вынуждающей силы совпадет с собственной частотой колебаний маятника (явление резонанса). Собственная частота колебаний равна:  , частота вынуждающей силы  . Следовательно, частоту вынуждающей силы необходимо уменьшить в 5 раз.