Билет 13.

1. Ремонтопригодность восстанавливаемых технических систем и ее характеристики.

Характеристики ремонтопригодности:

1) Вероятность восстановления в заданное время.

V()=P(T_B<)

V()=1-e^-

 - интенсивность восстановления – характеризует производительность ремонтного подразделения.

Продолжительность ремонта складывается из 2-х составляющих:

1) поиск места от истца

2) ремонт

Статические оценки характеристики надежности:

1) среднее время (мат. ожидание) наработки на отказ

2) Мат. ожидание времени восстановления

;

2. Биномиальное распределение и его применение в теории надежности.

Пусть имеется конечная последовательность n случайных величин:

x₁, x₂, … , x_n,

каждая из которых имеет распределение Бернулли:

,

Биномиальное распределение определяет, какое количество интересующих нас исходов будет в n-испытаниях.

n – количество членов конечной последовательности

m – число исходов

P_nm – вероятность ровно m исходов при n испытаниях

Р – вероятность события

Билет 14.

1. Долговечность восстанавливаемых технических систем и ее характеристики.

Определения 1.3, показатели долговечности 6.15, 6.17.

2. Оценивание интенсивности отказов при хранении и работе технических систем по результатам опытной эксплуатации.

P(t)=P(tхр)P(tр)

Определить интенсивность отказов при хранении, как правило, не представляется возможным, потому что при проверке хранимых на складе объемов авиационной техники мы по результатам проверки можем только фиксировать работоспособность/неработоспособность того или иного объекта, но на каком этапе он отказал, сказать не можем.

Методика определения:

(*)

Для определения λхр и λр ведется наблюдение за 2-мя партиями однотипных изделий. При этом количество объектов в партиях может быть и одинаковым, и разным. А вот время хранения до проверки должно принципиально отличаться. Очевидно, что процент отказавших в той партии, которая хранилась дольше, будет больше из-за повышенного количества отказов на этапе хранения.

N₁, N₂ – количество объектов в первой и во второй партиях.

t_хр1, t_хр2 – время хранения до проверки.

t_p1, t_p2 – время проверки.

N_отк1, N_отк2 – количество выявленных отказов.

Распишем (*) для двух партий.

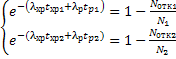
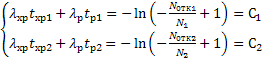
Математическое ожидание числа отказавших:

МО_хр=λ_хрt_хр; МО_р=λ_рt_р.

Билет 15.

1. Сохраняемость технических систем и ее характеристики.

Определения 1.5, 6.24.

2. Расчет безотказности технических систем с использованием ключевого элемента.

Методика расчета с использованием ключевого элемента:

1) В рассматриваемой схеме выбирается один или несколько ключевых элементов. В качестве ключевого элемента целесообразно выбирать такой, который имеет максимальное число связей с другими элементами (3 элемент).

2) Для ключевого элемента принимаются 2 гипотезы в отношении его работоспособности:

Hip1 – элемент работоспособен.

Hip2 – элемент неработоспособен.

3) Исходная схема изображается для условий рассматриваемой гипотезы:

Hip1

Hip2

4) Применяется формула полной вероятности:

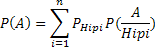
Для нашего случая, P_Hip1=P₃; P_Hip2=1-P₃.