Частотный критерий устойчивости Найквиста при наличии в структуре разомкнутой ас интегрирующих звеньев.
При исследовании устойчивости считается по известной передаточной функции разомкнутой АС. Заменяем S на j и тем самым получаем комплексную передаточную функцию (КПФ) . При изменении вектор КПФ будет вычерчивать кривую – годограф КПФ. По виду этой кривой для разомкнутой АС можно судить о устойчивости замкнутой АС.
Существует 3 случая исследования устойчивости по Найквисту:
1 случай: Разомкнутая АС устойчива
2 случай: Разомкнутая АС нейтрально устойчива( на границе устойчивости) и имеет в своем составе интегрирующих звеньев.
3 случай: Разомкнутая АС неустойчива и имеет m правых полюсов ( m корней характеристического уравнения с положительными вещественными частями.
2 случай: Нейтрально устойчивая АС
П
Ф
можно представить в виде
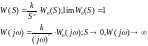
Т.к.
годограф КПФ начинается в бесконечности
трудно судить охватывает ли годограф
КПФ разомкнутой АС критическую точку
или нет. Для разрешения этого вопроса
введем дугу бесконечного радиуса с
угловой координатой омега
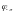
Полученную таким образом дугу назовем дополнением. Для устойчивости замкнутой АС в случае нейтрально устойчивой разомкнутой АС и имеющей интегрирующих звеньев необходимо и достаточно чтобы годограф КПФ разомкнутой АС вместе с дополнением не охватывал критическую точку.
Частотный критерий устойчивости Найквиста в случае неустойчивой замкнутой ас. Обобщенный критерий устойчивости Цыпкина.
При исследовании устойчивости считается по известной передаточной функции разомкнутой АС. Заменяем S на j и тем самым получаем комплексную передаточную функцию (КПФ) . При изменении вектор КПФ будет вычерчивать кривую – годограф КПФ. По виду этой кривой для разомкнутой АС можно судить о устойчивости замкнутой АС.
Существует 3 случая исследования устойчивости по Найквисту:
1 случай: Разомкнутая АС устойчива
2 случай: Разомкнутая АС нейтрально устойчива( на границе устойчивости) и имеет в своем составе интегрирующих звеньев.
3 случай: Разомкнутая АС неустойчива и имеет m правых полюсов ( m корней характеристического уравнения с положительными вещественными частями.
2 случай: Нейтрально устойчивая АС
В этом случае трудно судить охватывает ли годограф КПФ разомкнутой АС критическую точку или нет. Для разрешения этого вопроса введем бесконечного радиуса с угловой координатой омега
Полученную таким образом дугу назовем дополнением. Для устойчивости замкнутой АС в случае нейтрально устойчивой разомкнутой АС и имеющей интегрирующих звеньев необходимо и достаточно чтобы годограф КПФ разомкнутой АС вместе с дополнением не охватывал критическую точку.
3 случай: Разомкнутая АС неустойчива и имеет m правых полюсов ( m корней характеристического уравнения с положительными вещественными частями.
В
окрестности критической точки в этом
случае получается сложная картина
поведения годографа разомкнутой АС
(петли самопересечения. В этом случае
используется обобщенный критерий
устойчивости Ципкина.
П
ереход
годографа КПФ слева от критической
точки снизу вверх обознчают «П-» и
называют отрицательным переходом,
сверху вниз-положительным переходом
«П+». Для устойчивости замкнутой АС в
случае неустойчивой разомкнутой АС и
имеющей в своем составе m
правых полюсов (m корней
характеристического уравнения разомкнутой
АС) необходимо и достаточно чтобы
разность между положительным и
отрицательным переходами была равна
Если годограф КПФ начинается на отрезке слева от критической точки то переход равен +-1/2. + если вверх,- если вниз идет.
